Fragenliste von Einfache Kinematik
|
Ein Auto fährt \(5\quad \mathrm{Minuten}\) mit der Geschwindigkeit \(100 \ \frac{km}{h}\) und anschließend für \(15\quad \mathrm{Minuten}\) mit der Geschwindigkeit \(160 \ \frac{km}{h}\). Welche Durchschnittsgeschwindigkeit hat das Auto? (Hinweis: Die Beschleunigungsphase ist so kurz, dass sie vernachlässigt werden kann.) Nr. 1531
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt innerhalb von \(10\) Sekunden gleichförmig von der Geschwindigkeit \(v_0 = 10 \ \frac{m}{s}$ \) auf die Geschwindigkeit \(v_1= 60 \ \frac{m}{s}\). Berechne die Beschleunigung \(a\) des Objekts. Nr. 1532
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto hat die Anfangsgeschwindigkeit \(v_0 = 30,0 \ \frac{km}{h}\) und beschleunigt in \(20,0\) Sekunden gleichförmig auf die Nr. 1534
|
|
|---|---|
| Lösungsweg | |
|
Ein sich mit konstanter Geschwindigkeit \(v\) in eine bestimmte Richtung \(x\) bewegendes Objekt folgt der Bewegungsgleichung (Ortsfunktion) \(x(t)=v t +x_0\), wobei \(x_0\) der Ort zum Zeitpunkt \(t=0\) ist. Im folgenden betrachten wir ein Objekt mit Geschwindigkeit \(v=5\ \frac{m}{s}\). Dieses Objekt befindet sich zudem zum Zeitpunkt \(t=10\, s\) am Ort \(x=20\,m\). Ermittle für diesen Fall \(x_0\). Nr. 1552
|
|
|---|---|
| Lösungsweg | |
|
Betrachte folgende Situation: Zwei Autos sind \(600\, m\) voneinander entfernt und fahren mit konstanter Geschwindigkeit direkt aufeinander zu. Die Geschwindigkeiten der jeweiligen Autos betragen hierbei \(10\, \frac{m}{s}\) (Geschwindigkeit des 1.Fahrzeugs) und \(20\, \frac{m}{s}\) (Geschwindigkeit des 2. Fahrzeugs). Nach wieviel Sekunden treffen die Autos aufeinander? Nr. 1588
|
|
|---|---|
| Lösungsweg | |
|
Betrachte folgende Situation: Zwei Züge sind \(2400\, m\) voneinander entfernt und fahren mit konstanter Geschwindigkeit direkt aufeinander zu. Dabei hat der erste Zug die Geschwindigkeit \(30\, \frac{m}{s}\), und der zweite \(50\, \frac{m}{s}\). Welche Strecke legen die beiden Züge jeweils bis zum Zusammenstoß zurück? Nr. 1591
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto fährt \(30\, s\) mit der Geschwindigkeit \(72\, \frac{km}{h}\) geradeaus, und danach \(48\, s\) mit \(36\, \frac{km}{h}\) in die selbe Richtung. Im Anschluss fährt es mit \(54\, \frac{km}{h}\) in entgegengesetzte Richtung zum Ausgangspunkt zurück. Wie lange dauert die Rückfahrt? Nr. 1592
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt innerhalb von \(5\) Sekunden gleichförmig von der Geschwindigkeit \(v_0 = 30 \ \frac{m}{s}$ \) auf die Geschwindigkeit \(v_1= 50 \ \frac{m}{s}\). Berechne die Beschleunigung \(a\) des Objekts. Nr. 1598
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt bewegt sich mit konstanter Geschwindigkeit in eine beliebige, jedoch fixierte Richtung. Es legt dabei in \(15\quad \mathrm{Minuten}\) eine Strecke von \(30\, km\) zurück. Welche Geschwindigkeit hat das Objekt in der entsprechenden SI-Einheit? Runde dabei sinnvoll. Nr. 1599
|
|
|---|---|
| Lösungsweg | |
|
Wir betrachten die Bewegung in einer Dimension. Ein Objekt der Masse \(m=1,85\, g\) bewegt sich mit konstanter Geschwindigkeit und legt dabei in \(4,46 \, s\) Sekunden eine Strecke von \(16,98\, m\) zurück. Welchen Impuls \(p\) hat das Objekt? Runde auf drei signifikante Stellen genau (Wie immer in der entsprechenden SI-Einheit)! Nr. 1600
|
|
|---|---|
| Lösungsweg | |
|
Wie schnell muss ein LKW mit einer Gesamtmasse von \(8,5 \, t\) fahren damit sein Impuls \(p\) den Wert \(170 \cdot 10^3\, \frac{kg \cdot m}{s}\) hat? (in SI-Einheiten) Nr. 1601
|
|
|---|---|
| Lösungsweg | |
|
Die Lichtgeschwindigkeit (welche üblicherweise das Formelzeichen \(c\) trägt) beträgt in etwa \(3,0 \cdot 10^8\ \frac{m}{s}\). Welche Strecke \(s\) (in Meter) legt demnach ein Lichtstrahl in einem Jahr zurück? (Hinweis: Es wird das sogenannte 'Lichtjahr' berechnet. Ein Lichtjahr ist somit keine Zeit wie der Name vermuten lassen könnte, sondern eine Länge bzw.Strecke) Nr. 1602
|
|
|---|---|
| Lösungsweg | |
|
Gleichförmige Bewegung Ein Körper bewegt sich mit konstanter Geschwindigkeit und legt in einer Zeit von \(\Delta t=2\, s\) eine Strecke von \(\Delta s = 8\, m\) zurück. Welche mit welcher Geschwindigkeit \(v\) bewegt sich der Körper? Nr. 1832
|
|
|---|---|
| Lösungsweg | |
|
Gleichförmige Bewegung Ein Körper bewegt sich mit konstanter Geschwindigkeit und legt in einer Zeit von \(\Delta t=5\,s\) eine Strecke von \(\Delta s = 3\,m\) zurück. Welche mit welcher Geschwindigkeit \(v\) bewegt sich der Körper? Nr. 1833
|
|
|---|---|
| Lösungsweg | |
|
Fußballer Marko A. verliert in Spielminute \(36\,:\,00\) den Ball \(5\,m\) vor dem gegnerischen Tor und beginnt mit konstanter Geschwindigkeit (parallel zur Seitenoutlinie) zurückzu"laufen". In Minute \(37\,:\,00\) kommt er \(10\,m\) vor der eigenen Torlinie zu einem Eckball an. Das Fußballfeld ist genau \(105\,m\) lang. Wie schnell ist er "gelaufen"? Nr. 1834
|
|
|---|---|
| Lösungsweg | |
|
Gib folgende Geschwindigkeit in der SI Einheit für Geschwindigkeiten an: \(130\ \frac{km}{h}\) Nr. 1836
|
|
|---|---|
| Lösungsweg | |
|
Gib folgende Geschwindigkeit in der SI Einheit für Geschwindigkeiten an: \(41\ Knoten=41\ \frac{Seemeilen}{ Stunde}=41\ \frac{sm}{h}\) (Geschwindigkeit des sowjetischen U-Boots: "Projekt 705 Lima"; eines der schnellsten U-Boote, das jemals gebaut wurde) \(1\ Seemeile=1\ sm=1852\ m\) Nr. 1837
|
|
|---|---|
| Lösungsweg | |
|
Gleichförmig beschleunigte Bewegung Ein Student,der mit \(1,4\ \frac{m}{s}\) geht, sieht, dass seine Straßenbahn kommt und beginnt zu laufen. Dabei beschleunigt er (gleichförmig) in \(2\,s\) auf \(5,4\ \frac{m}{s}\). Wie groß ist die Beschleunigung \(a\) des Studenten? Nr. 1838
|
|
|---|---|
| Lösungsweg | |
|
Usain Bolt beschleunigt beim Start eines Sprints in \(t=2\,s\) von \(v_1=0\ \frac{km}{h}\) auf \(v_2=36\ \frac{km}{h}\). Wie hoch ist seine Beschleunigung \(a\) (in der Annahme, dass er gleichförmig beschleunigt)? Nr. 1839
|
|
|---|---|
| Lösungsweg | |
|
Ein Zug bremst (gleichförmig) in \(50\,s\) von \(v_1=180\ \frac{km}{h}\) auf \(v_2=0\ \frac{km}{h}\). Gib die Beschleunigung \(a\) an, die auf die Fahrgäste wirkt. Nr. 1840
|
|
|---|---|
| Lösungsweg | |
|
Ein Porsche Ruf 911 PDK beschleunigt in \(t=2,72\,s\) von \(v_1=0\ \frac{km}{h}\) auf \(v_2=100\ \frac{km}{h}\). Wie hoch ist die Beschleunigung \(a\) (unter der Annahme, dass eine gleichförmige Beschleunigung vorliegt)? Nr. 1841
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung: \(x(t)=9t^2+24\) Wann ist der Körper bei \(x=60\,m\)? Nr. 2037
|
|
|---|---|
| Lösungsweg | |
|
Welche Näherungsformel kann verwendet werden, um die Tiefe \(h\) eines Brunnens abzuschätzen? Dabei ist \(t\) die Zeit, die vergeht zwischen dem Loslassen eines Steines, den man in den Brunnen fallen lässt, und dem Hören des Aufprallgeräusches, \(g\) ist die Erdbeschleunigung, \(c\) die Schallgeschwindigkeit. Nr. 2105
|
|
|---|---|
| Lösungsweg | |
|
Ein Gepard benötigt \(3 \mathrm{\ Sekunden}\), um aus dem Stand auf seine Höchstgeschwindigkeit von \(122\ \frac{km}{h}\) zu kommen. Wer beschleunigt schneller? Nr. 3100
|
|
|---|---|
| Lösungsweg | |
|
Herr X fährt mit seinem Auto von Zuhause weg. Er fährt zunächst \(20\mathrm{\ Minuten}\) mit \(30\ \frac{km}{h}\), dann \(10\mathrm{\ Minuten}\) mit \(80\ \frac{km}{h}\) und danach \(30\mathrm{\ Minuten}\) mit \(50\ \frac{km}{h}\). Hinweis: Die Beschleunigungszeiten dazwischen sind als so gering angenommen, dass sie vernachlässigt werden. Nr. 3101
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt gleichmäßig aus dem Stand mit \(4\ \frac{m}{s^2}\) und das auf einer Strecke von \(30\, m\). Wie lange braucht das Objekt für diese Strecke? Nr. 3102
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt gleichmäßig aus dem Stand mit \(6\ \frac{m}{s^2}\). Nr. 3103
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt gleichmäßig aus dem Stand mit \(3,9\ \frac{m}{s^2}\). Welche Geschwindigkeit hat es nun erreicht? Nr. 3104
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt legt in der Zeit \(t=30\,min\) einen Weg \(s=8,57\,km\) zurück. Mit welcher durchschnittlichen Geschwindigkeit \(v\) bewegt sich das Objekt fort? Nr. 3123
|
|
|---|---|
| Lösungsweg | |
|
Welchen Impuls hat ein LKW mit einer Masse \(m=9,3\,t\) wenn er mit einer Geschwindigkeit \(v=30\ \frac{km}{h}\)gegen eine Wand fährt? Nr. 3125
|
|
|---|---|
| Lösungsweg | |
|
Zwei Autos sind \(s=900\,m\) von einander entfernt. Gleichzeitig beginnen sie aufeinander zuzufahren. Auto A fährt mit \(v_A=50\ \frac{km}{h}\) und Auto B mit \(v_B=30\ \frac{km}{h}\). Nach welcher Zeit \(t\) kollidieren die zwei Fahrzeuge? Nr. 3133
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto beschleunigt gleichförmig in \(t=15\,s\) von \(0-100\ \frac{km}{h}\). Welche Strecke \(s\) legt das Auto während der Beschleunigungsphase zurück? Nr. 3134
|
|
|---|---|
| Lösungsweg | |
|
Oft spricht man von einem Lichtjahr, die Distanz, die Licht in einem Jahr zurücklegt. Die Geschwindigkeit von Schall beträgt bei trockener Luft etwa \(v=342,2\ \frac{m}{s}\). Wie weit kommt also Schall in einem Jahr? Hinweis: Es gibt keinerlei Hindernisse und die Lufteigenschaften seien konstant. Nr. 3135
|
|
|---|---|
| Lösungsweg | |
|
Eine Radfahrerin fährt mit ihrem Rad mit \(v_1=30\ \frac{km}{h}\) für die Zeit \(t_1=20\,min\). Gleich danach fährt sie \(t_2=5\,min\) lang mit der Gechwindigkeit \(v_2=35\ \frac{km}{h}\) und am Schluss zum Entspannen \(t_3=30\,min\) lang mit der Geschwindigkeit \(v_3=15\ \frac{km}{h}\). Wie groß ist ihre Durchschnittsgeschwindigkeit \(v\)? Hinweis: Bremswege können vernachlässigt werden Nr. 3136
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto fährt mit einer konstanten Geschwindigkeit \(v=43\ \frac{km}{h}\) gerade aus. Nr. 3137
|
|
|---|---|
| Lösungsweg | |
|
Ein LKW \((m=7,3\,t)\) beschleunigt für \(t_1=20\,s\) mit \(a=2,5\ \frac{m}{s^2}\). Genau bei \(t_2=80\,s\) wäre der LKW fast gegen eine Wand gefahren. Welchen Impuls hätte er gehabt? Nr. 3183
|
|
|---|---|
| Lösungsweg | |
|
Die Erdbeschleunigung \(g\) kann man mithilfe eines mathematischen Pendels überprüfen. Wie lange dauert also ein Pendelschwung \(T_0\), wenn die Fadenlänge \(l=8\,cm\) beträgt? Nr. 3294
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt bewegt sich mit der Geschwindigkeit \(v=100\ \frac {km}{h}\). Welche Masse \(m \) benötigt das Objekt um einen Impuls \(p=1,6\cdot 10^4 \quad\frac{kg\cdot m}{s}\) mitzubringen? Nr. 3295
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto beschleunigt gleichförmig in der Zeit \(t=5\,s\) von der Geschwinigkeit \(v_1=30\ \frac{km}{h}\) auf \(v_2=100\ \frac{km}{h}\). Berechne die durchschnittliche Beschleunigung \(a\). Nr. 3321
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto benötigt eine Zeit \(t=3,9\,s\) um von \(0-100\ \frac{km}h}\) kommen und beschleunigt dabei gleichförmig. Berechne die Beschleunigung \(a\). Nr. 3322
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt mit \(a=7,5\ \frac{m}{s^2}\). Wie lange braucht das Objekt, um von \(v_0=10\ \frac{m}{s}\) auf \(v_1=35\ \frac{m}{s}\) gleichförmig zu beschleunigen? Nr. 3323
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto wird mit \(a=4,7\ \frac{m}{s^2}\) aus dem Stillstand für \(t=9\,s\) gleichförmig beschleunigt. Welche Geschwindigkeit \(v\) hat das Auto nach \(9\mathrm{\ Sekunden}\) erreicht? Nr. 3324
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto beschleunigt von \(v_1=30\ \frac{km}{h}\) auf \(v_2=90\ \frac{km}{h}\) gleichmäßig mit \(a=2,9\ \frac{m}{s^2}\). Wie lange braucht es dafür? Nr. 3325
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt beschleunigt gleichmäßig in \(t=5,35\,s\) von \(v_1=10\ \frac{km}{h}\) auf \(v_2=100\ \frac{km}{h}\). Berechne die durchschnittliche Beschleunigung \(a\). Nr. 3326
|
|
|---|---|
| Lösungsweg | |
|
Wie lange braucht ein Auto mit einer konstanten Beschleunigung \(a=4,9\ \frac{m}{s^2}\) um von \(v_1=15\ \frac{m}{s}\) auf \(v_2=30\ \frac{m}{s}\) zu kommen? Nr. 3327
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt erfährt eine Beschleunigung \(a=8,6\ \frac{m}{s^2}\) und beschleunigt von \(v_1=5\ \frac{m}{s}\) auf \(v_2=30\ \frac{m}{s}\). Wie lange braucht es dafür? Nr. 3328
|
|
|---|---|
| Lösungsweg | |
|
Ein Motorrad beschleunigt gleichförmig aus dem Stand mit \(a=5,97\ \frac{m}{s^2}\) für die Zeit \(t=5\,s\). Welche Geschwindigkeit \(v\) hat das Motorrad zum Zeitpunkt \(t=5\,s\) erreicht? Nr. 3329
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt wird durch eine Kraft mit \(a=6,22\ \frac{m}{s^2}\) aus dem Stand für eine Zeit \(t=6\,s\) gleichförmig beschleunigt. Welche Geschwindigkeit \(v\) erreicht das Objekt nach der Beschleunigungsphase. Nr. 3330
|
|
|---|---|
| Lösungsweg | |
|
Zwei Autos sind \(1800\, m\) voneinander entfernt. Sie fahren zum selben Zeitpunkt los. Wie lange brauchen die Fahrzeuge um aufeinander zu treffen? Hinweis: Die Beschleunigungsphase der Autos kann vernachlässigt werden. Nr. 3331
|
|
|---|---|
| Lösungsweg | |
|
Zwei Objekte bewegen sich mit konstanter Geschwindigkeit aufeinander zu. Objekt A hat eine Geschwindigkeit \(v_A=20\ \frac{m}{s}\) und Objekt B hat die Geschwindigkeit \(v_B=30\ \frac{m}{s}\). Wie weit waren sie zu Beginn voneinander entfernt? Nr. 3332
|
|
|---|---|
| Lösungsweg | |
|
Florian und Hanna stehen sich \(300\,m\) gegenüber und gehen aufeinander zu. Flo geht mit \(v_F=2,7\ \frac{m}{s}\) und Hanna mit \(v_H=1,9\ \frac{m}{s}\). Wielange dauert es, bis sie sich treffen? Hinweis: Die "Beschleunigungsphase" kann vernachlässigt werden. Nr. 3333
|
|
|---|---|
| Lösungsweg | |
|
Hans und Katrin wohnen \(s=8\,km\) voneinander entfernt. Sie beschließen gleichzeitig mit ihren Fahrzeugen aufeinander zu zufahren - Hans mit dem Fahrrad und Katrin mit dem Auto. Nach \(t=3\,min\) treffen sie sich und Hans erzählt, dass er konstant mit \(v_H=25\ \frac{km}{h}\) gefahren ist. Katrin ist sich nicht mehr sicher. Wie schnell ist Katrin gefahren? Hinweis: Beschleunigungsphasen können vernachlässigt werden. Nr. 3334
|
|
|---|---|
| Lösungsweg | |
|
Zwei Objekte sind \(s=650\,m\) voneinander entfernt und bewegen sich aufeinander zu. Objekt A bewegt sich mit \(v_A=8\ \frac{m}{s}\) fort und Objekt B mit \(v_B=5\ \frac{m}{s}\). Wie lange dauert es, bis sie aufeinander treffen? Nr. 3335
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto fährt mit einer konstanten Geschwindigkeit \(v_1=30\,\frac{km}{h} \) für eine Zeit \(t_1=20\,min\) gerade aus und danach für \(t_2=10\,min\) mit \(v_2=50\,\frac{km}{h}\). Nun kehrt das Auto zurück zum Ausgangspunkt mit einer Geschwindigkeit \(v_3=20\,\frac{km}{h}\). Wie lange dauert die Rückfahrt? Hinweis: Beschleunigungsphasen dazwischen können vernachlässigt werden Nr. 3336
|
|
|---|---|
| Lösungsweg | |
|
Ein Fahrradfahrer fährt für \(t_1=15\,min\)mit der Geschwindigkeit \(v_1=12\ \frac{km}{h}\) von seinem Haus weg. Danach fährt er mit der Geschwindigkeit \(v_2=25\ \frac{km}{h}\) für \(t_2=30\,min\). Zum Schluss fährt er mit \(v_3=32\ \frac{km}{h}\) für \(t_3=25\,min\). Wie weit ist er insgesamt gefahren? Hinweis: Die Straße, auf der er fährt, verläuft nur gerade aus und die Beschleunigungsphasen können vernachlässigt werden.
Nr. 3337
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto fährt \(t_1=15\,min\) mit \(v_1=30\,\frac{km}{h}\) gerade aus. Danach fährt es \(t_2=10\,min\) mit \(v_2=50\,\frac{km}{h}\). Nun fährt das Auto mit \(v_3=25\,\frac{km}{h}\) zurück zum Ausgangsort. Wie lange dauert die Heimreise? Nr. 3338
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt bewegt sich auf einer geraden Bahn mit einer Geschwindigkeit \(v_1=20\ \frac{m}{s}\) für \(t_1=5\,min\). Danach verdoppelt sich die Geschwindigkeit des Objektes für \(t_2=10\,min\). Am Schluss wird die Anfangsgeschwindigkeit \(v_1\) halbiert und das Objekt bewegt sich mit dieser Geschwindigkeit für \(t_3=20\,min\). Wie weit hat sich das Objekt vom Ausganspunkt entfernt, wenn es immer nur gerade aus gefahren ist? Nr. 3339
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto fährt mit der Geschwindigkeit \(v_1=10\ \frac{m}{s}\) für die Zeit \(t_1=50\,s\) gerade aus. Danach fährt das Auto mit \(v_2=25\ \frac{m}{s}\) für \(t_2=30\,s\). Nun entscheidet der Autofahrer mit \(v_R=20\ \frac{m}{s}\) zum Ausgangspunkt zurückzukehren. Wie lange braucht er für den Retourweg? Nr. 3340
|
|
|---|---|
| Lösungsweg | |
|
Die Bewegung eines Objekts kann durch die Bewegungsgleichung \(s(t)=8t^2+5t+9\) beschrieben werden. Wie weit ist das Objekt nach \(60\mathrm{\ Sekunden}\) gekommen? Nr. 3341
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt braucht genau \(t=1,3\,min\), um eine Strecke \(s=0,7\,km\) zurückzulegen. Mit welcher Geschwindigkeit \(v\) ist das Objekt unterwegs? Nr. 3346
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt benötigt \(t=0,5\,min\), um eine Strecke \(s=23\,cm\) zurückzulegen. Mit welcher durchschnittlichen Geschwindigkeit \(v\) bewegt sich das Objekt fort? Nr. 3347
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt bewegt sich mit einer Geschwindigkeit \(v=0,5\ \frac{m}{s}\). Wie lange braucht es also für eine Strecke mit einer Länge \(s=132\,mm\) ? Nr. 3348
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt fällt für eine Zeit \(t=4\,s\) aus einem Flugzeug, welches sich auf einer Höhe \(h=10\,\,000\,m\)befindet, und das Objekt beschleunigt mit der Erdbeschleunigung \(a=9,81\ \frac{m}{s^2}\). Welche Geschwindigkeit \(v\) hat das Objekt nun? Nr. 3489
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt fällt für eine Zeit \(t=4\,s\) aus einem Flugzeug, welches sich auf einer Höhe \(h=10\,\,000\,m\)befindet, und das Objekt beschleunigt mit der Erdbeschleunigung \(a=9,81\ \frac{m}{s^2}\). Auf welcher Höhe \(h\) befindet sich das Objekt nun? Nr. 3490
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto braucht \(t_1=6\,s\) um aus dem Stand eine Geschwindigkeit \(v=100\ \frac{km}{h}\) zu erreichen. Mit dieser berechneten Beschleunigung \(a\) beschleunigt das Fahrzeug gleichmäßig wiederum aus dem Stand für \(t_2=5\,s\). Welche Strecke \(s\) hat das Auto zum Zeitpunkt \(t_2\) zurückgelegt? Nr. 3491
|
|
|---|---|
| Lösungsweg | |
|
Ein Auto beschleunigt gleichmäßig aus dem Stand mit \(a=2,3\ \frac{m}{s^2}\) für eine Zeit \(t=9\,s\). Welche Strecke \(s\) hat das Auto während der Beschleunigungsphase zurückgelegt? Nr. 3492
|
|
|---|---|
| Lösungsweg | |
|
Ein Objekt bewegt sich für die Zeit \(t_1=11\,s\) mit der Geschwindigkeit \(v=8\,\frac{m}{s}\). Danach beschleunigt es gleichförmig mit \(a=2,2\ \frac{m}{s^2}\) für die Zeit \(t_2=5\,s\). Welche Strecke \(s\) hat das Objekt zurückgelegt? Nr. 3493
|
|
|---|---|
| Lösungsweg | |
|
Auf den geöffneten Fallschirm eines Fallschirmspringers wirke infolge des Luftreibung eine Bremsbeschleunigung \(a=-b v^2\) mit der Konstanten \(b=0,2\) . Wie groß ist die konstante Endgeschwindigkeit \(v_e\) des Springers? Nr. 4168
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bahnkurve \(\vec{r}(t)=\left(\begin{array}{c} t\\ \frac{1}{\sqrt{2}}t^{2}\\ \frac{1}{3}t^{3} \end{array}\right)\). Wie lautet der Ausdruck für die Krümmung \(\kappa(t)\) der Bahnkurve? Nr. 4172
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Lösung \(x(t)=A\cos\omega t+B\sin\omega t\) des linearen harmonischen Oszillators. Zu welcher Zeit \(t_0\) erreicht der Oszillator seinen maximal Ausschlag \(x_{Max}\)? Wie lautet der Ausdruck für \(x_{Max}\)? Nr. 4183
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Lösung \(x(t)=A\cos\omega t+B\sin\omega t\) des linearen harmonischen Oszillators. Zu welcher Zeit \(t_1\) erreicht der Oszillator seine Maximalgeschwindigkeit\(\dot{x}_{Max}\)? Wie lauten die jeweiligen Ausdrücke für die Maximalgeschwindigkeit \(\dot{x}_{Max}\) und die Maximalbeschleunigung \(\ddot{x}_{Max}\). Nr. 4184
|
|
|---|---|
| Lösungsweg | |
|
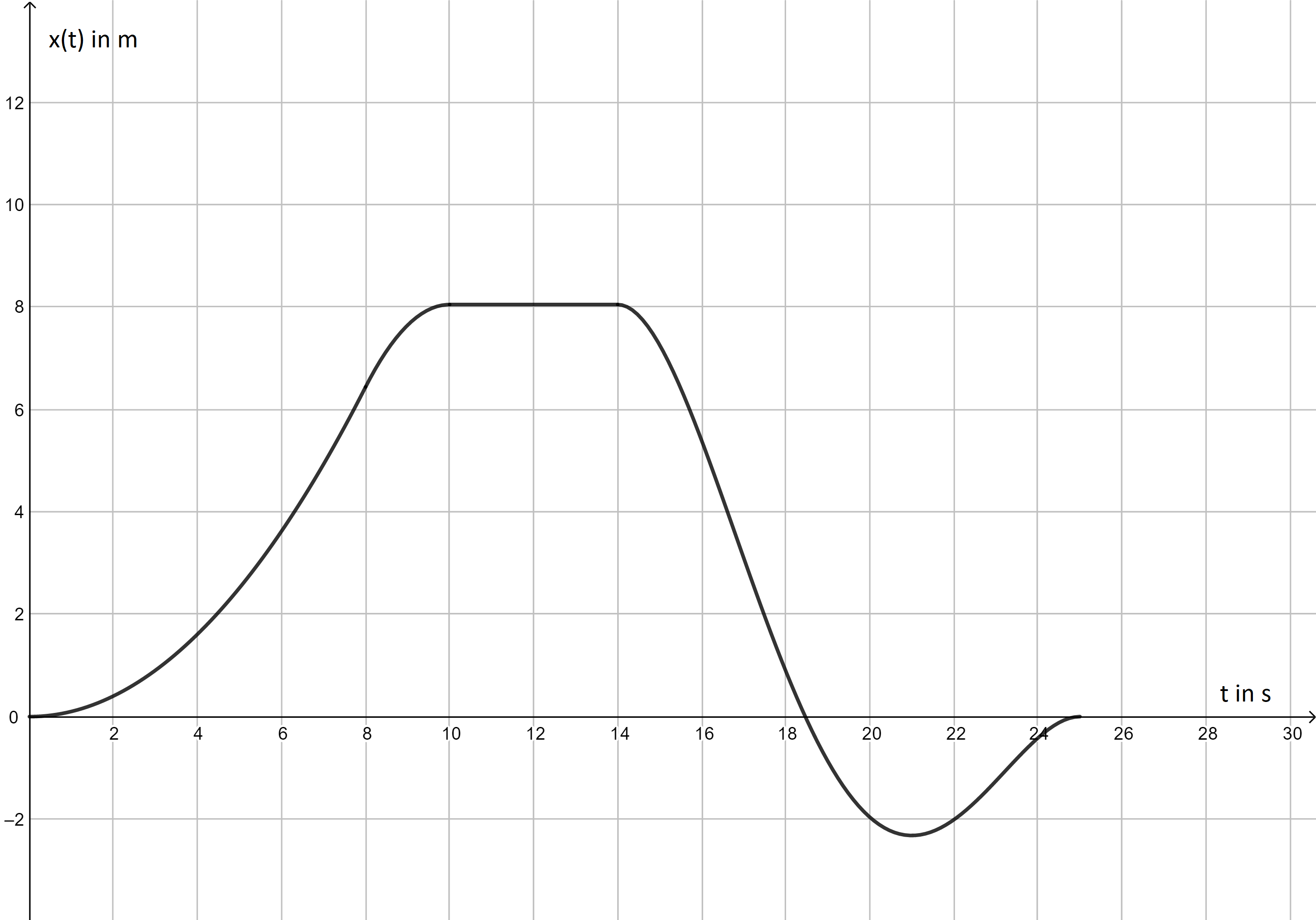
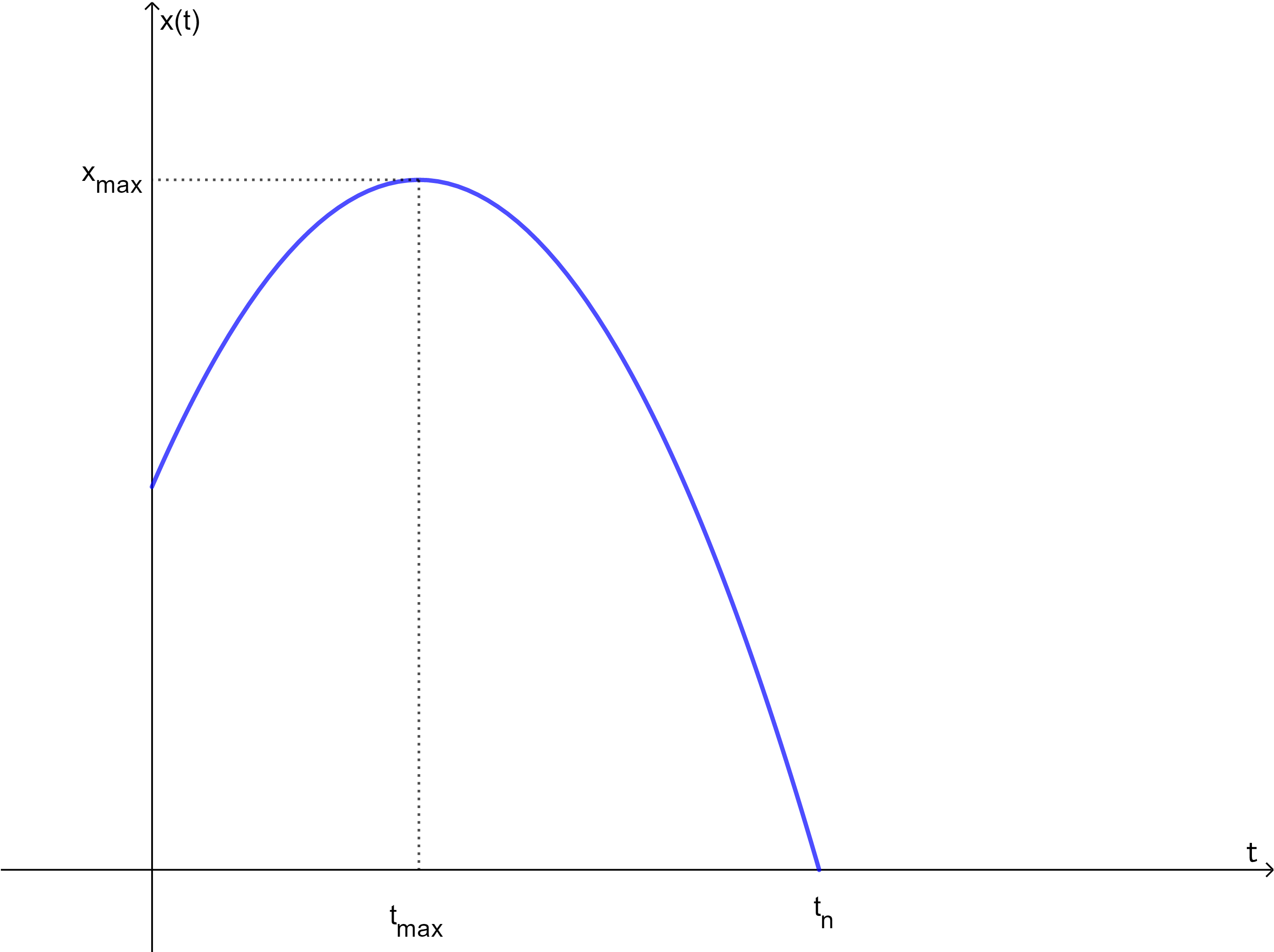
Betrachte folgendes Weg-Zeit-Diagramm, das eine geradlinige Bewegung eines Körpers in den Zeiten \(t \in \, [0,\ 25]\) (in Sekunden) beschreibt. Welche der Aussagen treffen/trifft zu? 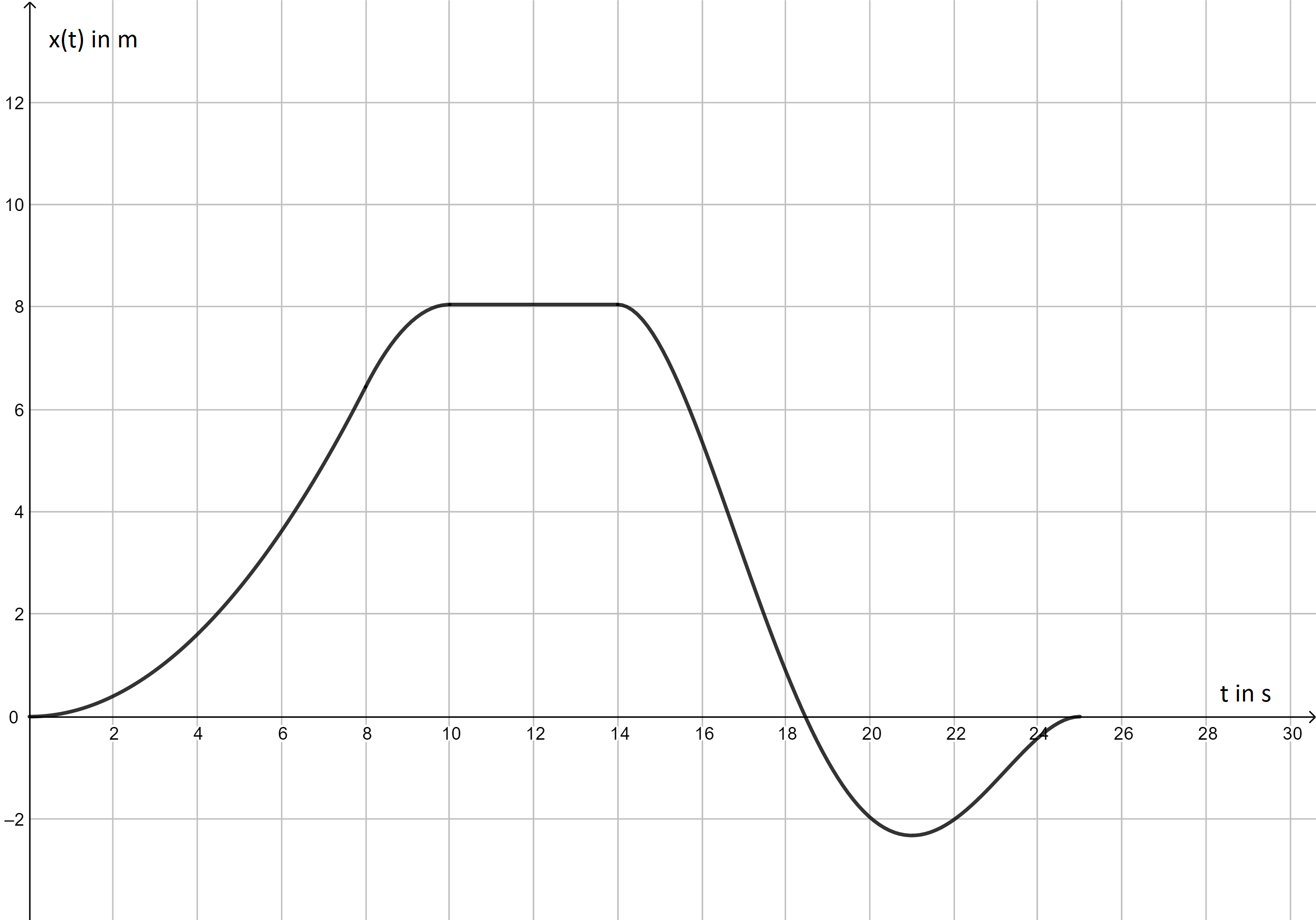 Nr. 4426
|
|
|---|---|
| Lösungsweg | |
|
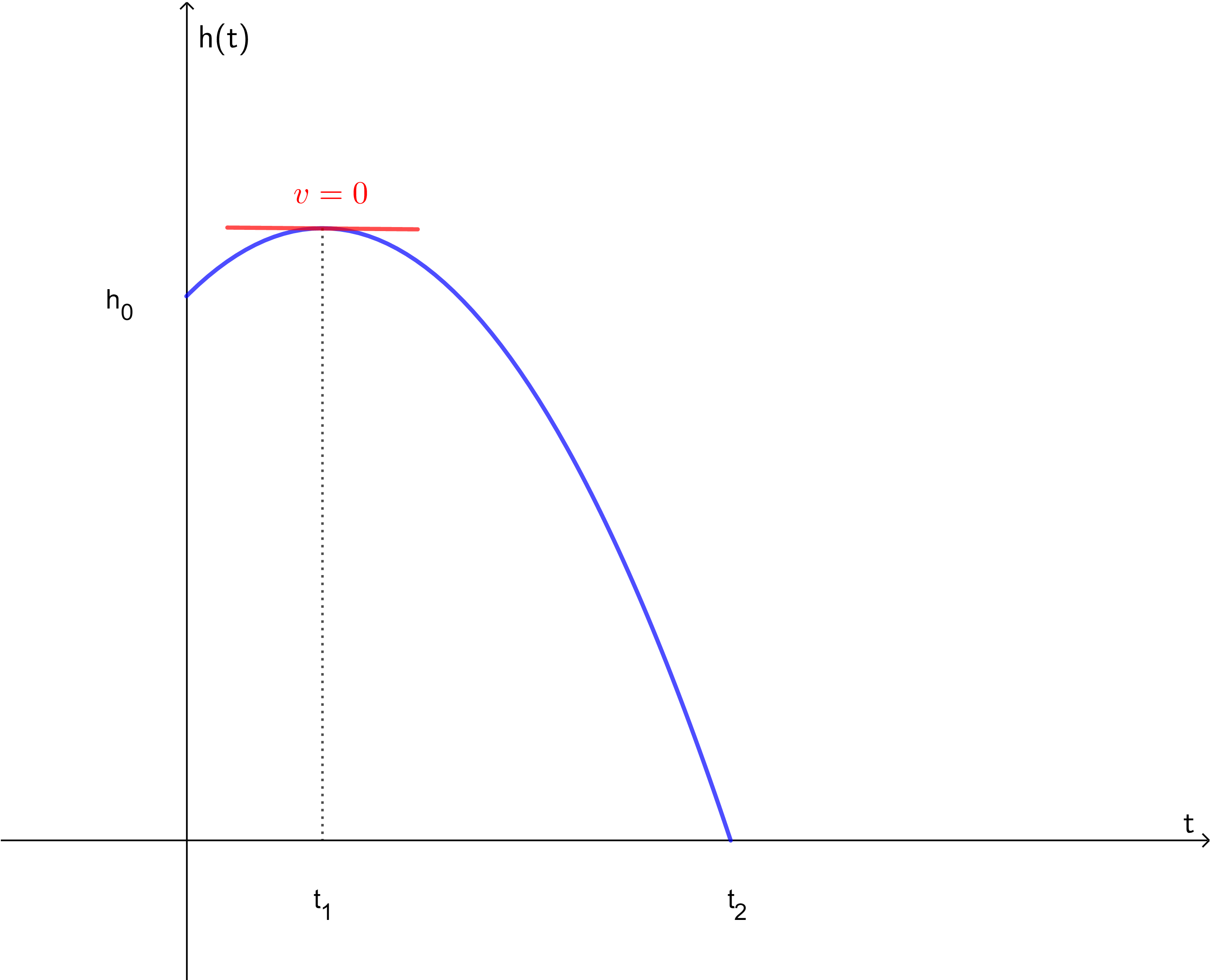
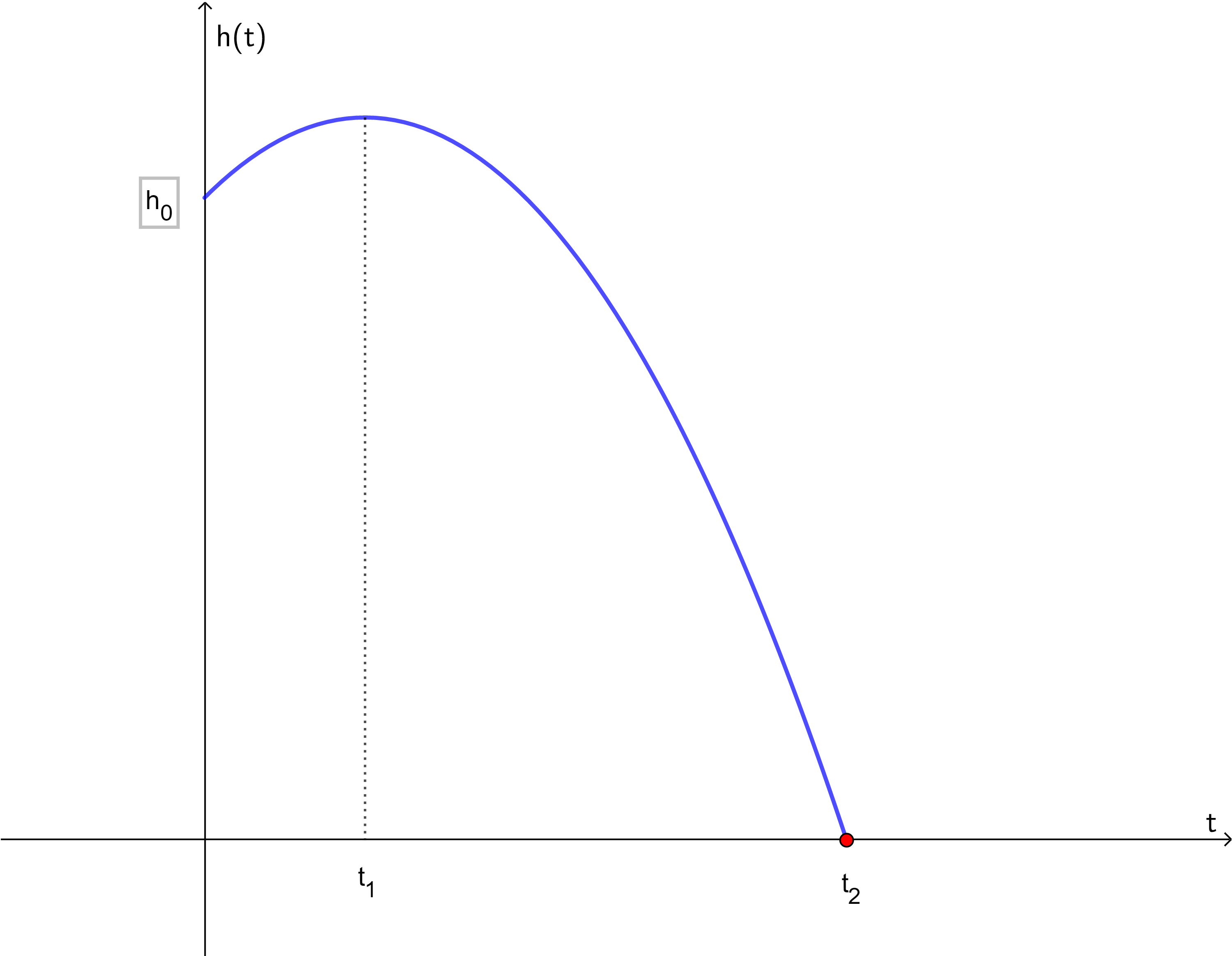
Ein Körper wird aus einer Höhe \(h_0=10\, m\) mit einer Geschwindigkeit \(v_0=5\ \frac{m}{s}\) senkrecht nach oben geworfen. Zu welchem Zeitpunkt \(t_1\) erreicht der Körper seine maximale Höhe? Rechne dabei mit \(g= 10\ \frac{m}{s^2}\). 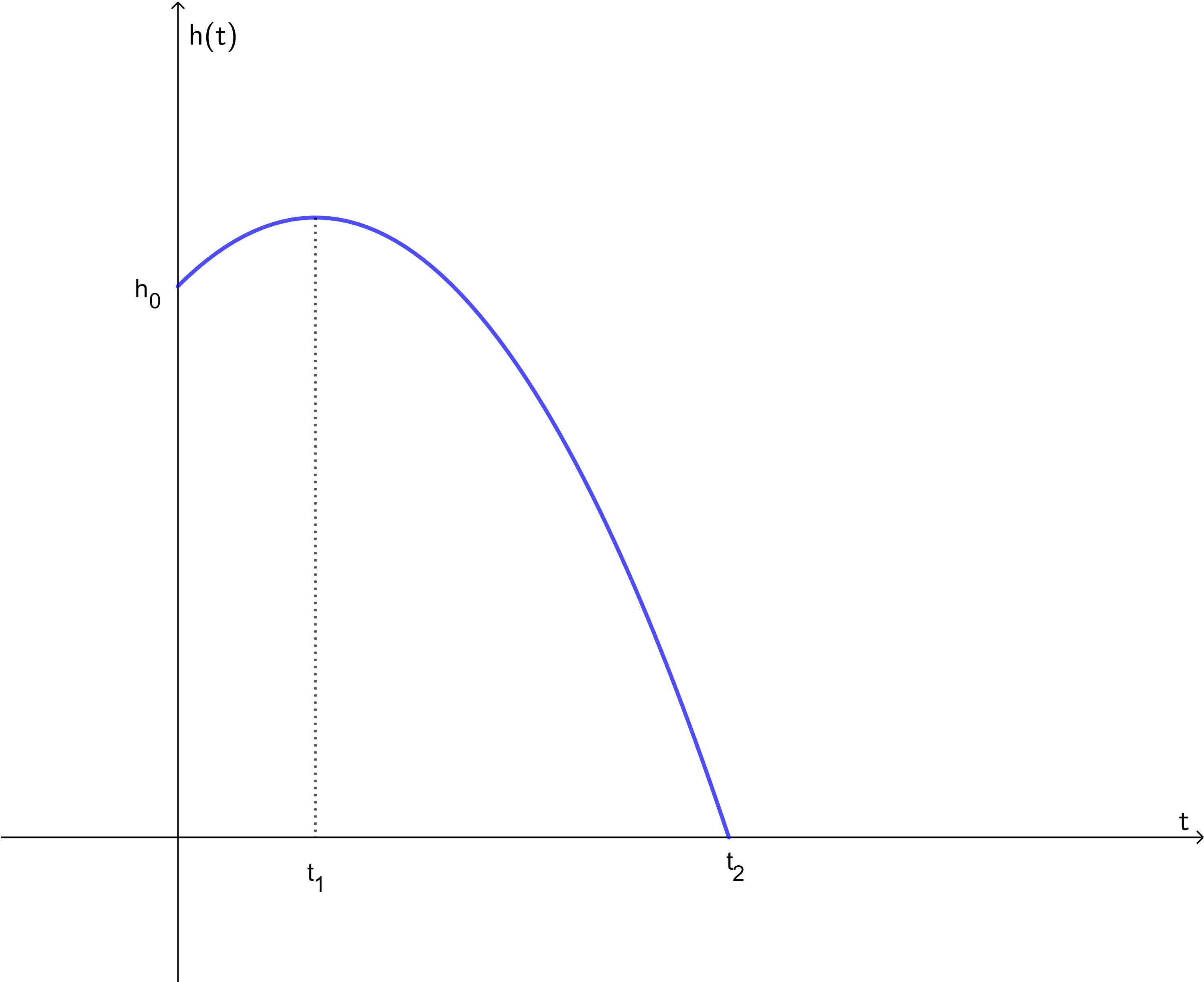 Nr. 4430
|
|
|---|---|
| Lösungsweg | |
|
Ein Körper wird aus einer Höhe \(h_0=10\, m\) mit einer Geschwindigkeit \(v_0=5\ \frac{m}{s}\) senkrecht nach oben geworfen. Zu welchem Zeitpunkt \(t_2\) erreicht der Körper den (Erd-)Boden? Rechne dabei mit \(g= 10\ \frac{m}{s^2}\). 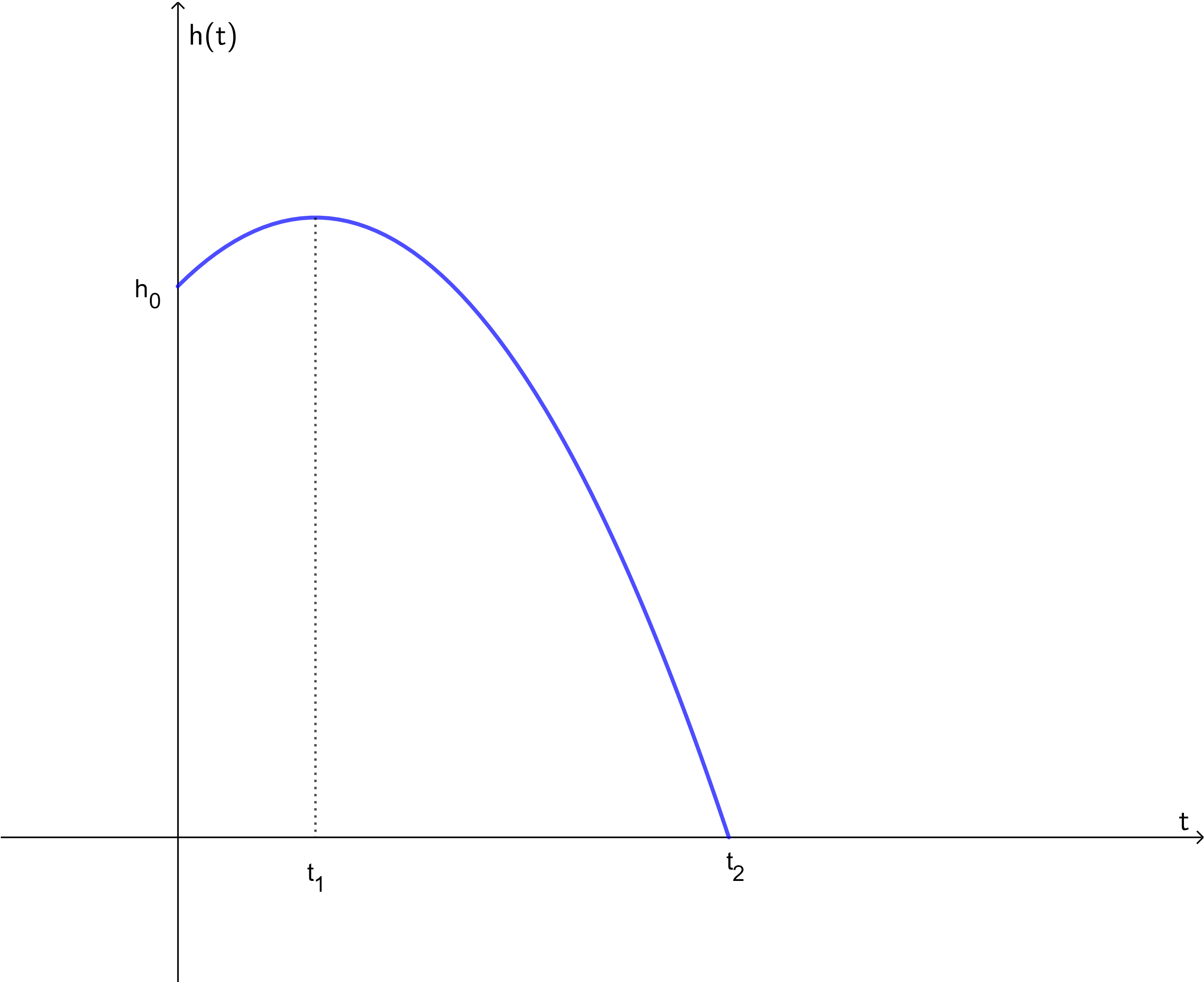 Nr. 4431
|
|
|---|---|
| Lösungsweg | |
|
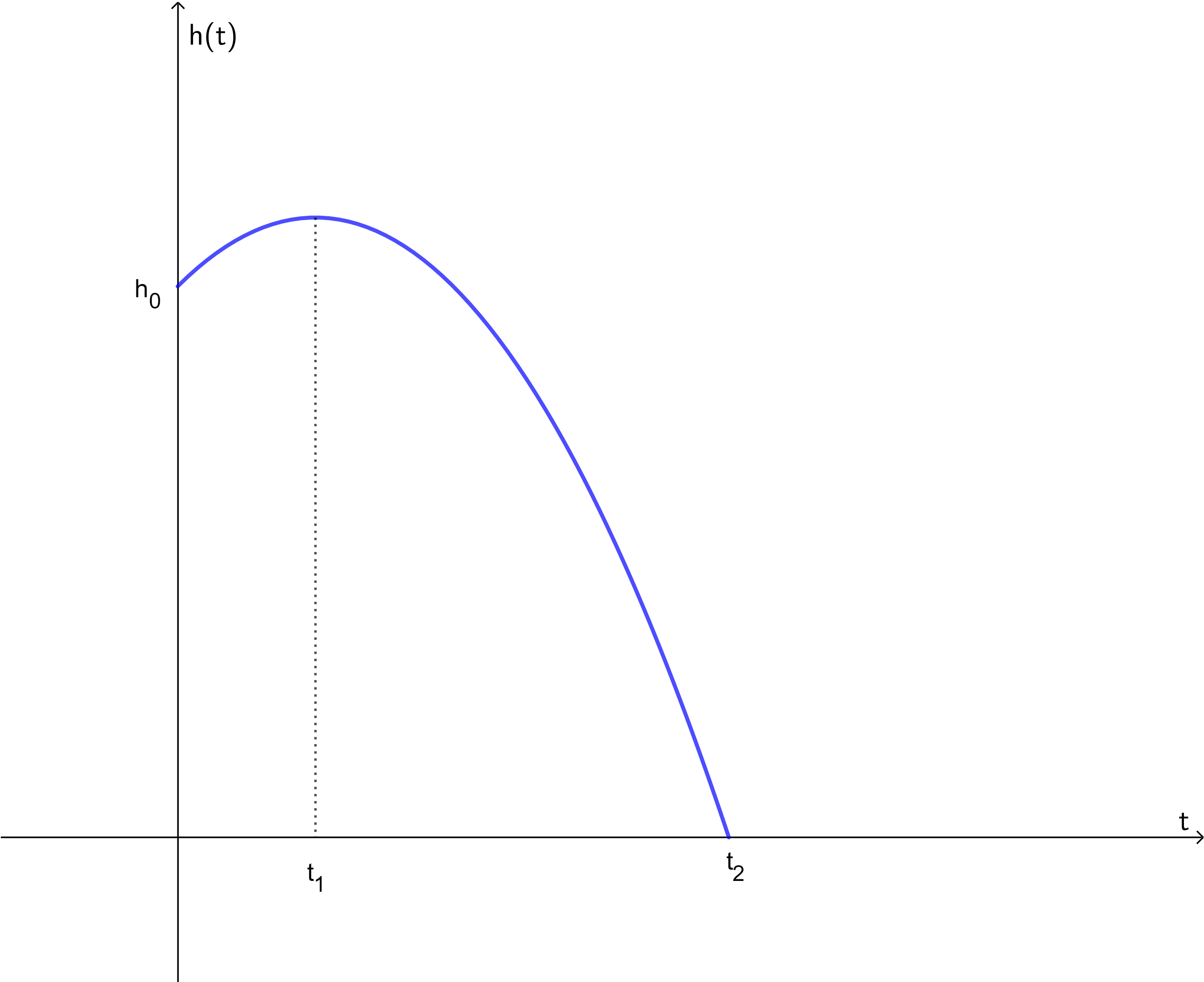
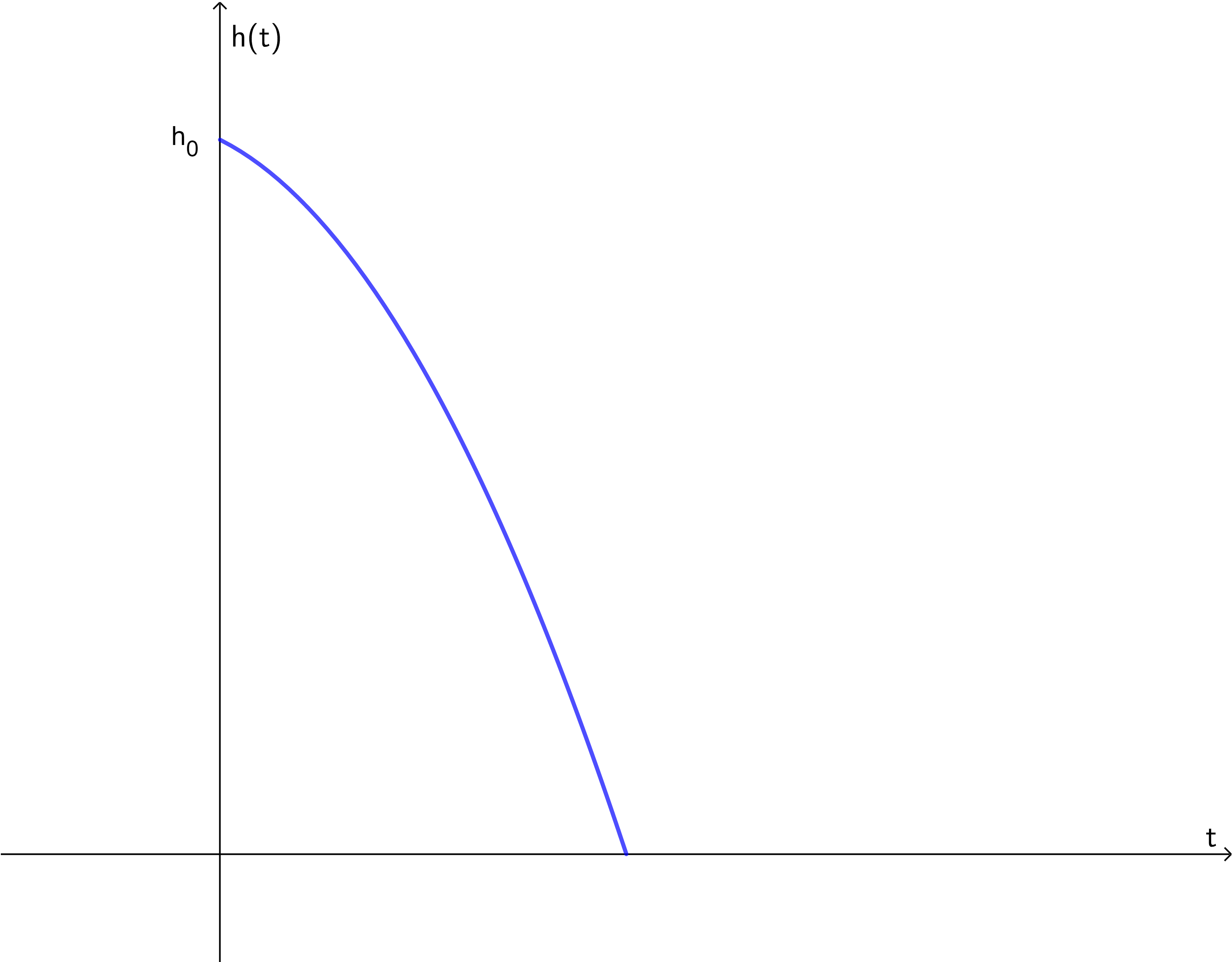
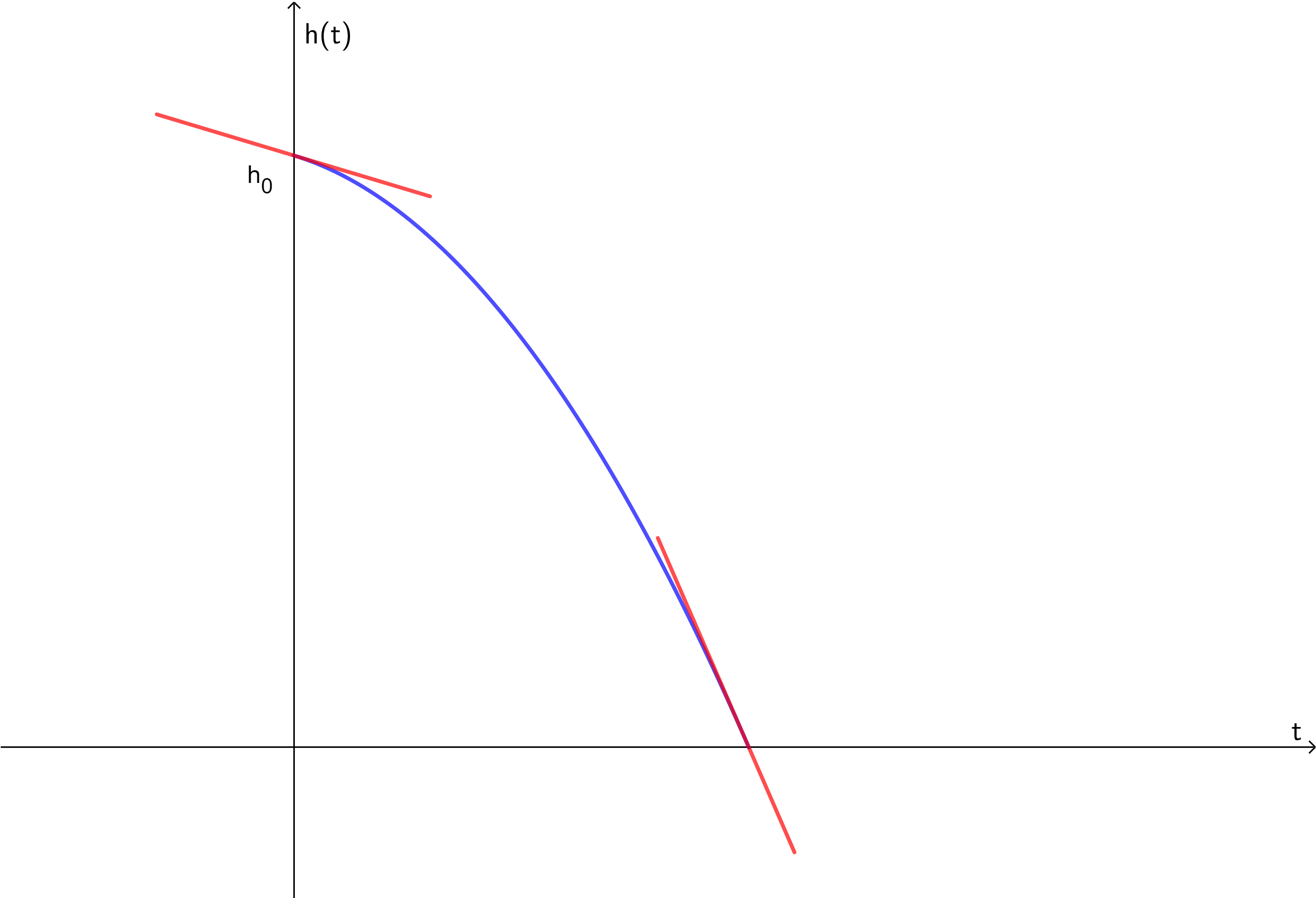
Ein Körper wird aus einer Höhe \(h_0\) mit einer Geschwindigkeit \(v_0\) senkrecht nach unten geworfen. Welches der folgenden Weg-Zeit-Diagramme beschreibt solch einen Fall? Nr. 4434
|
|
|---|---|
| Lösungsweg | |
|
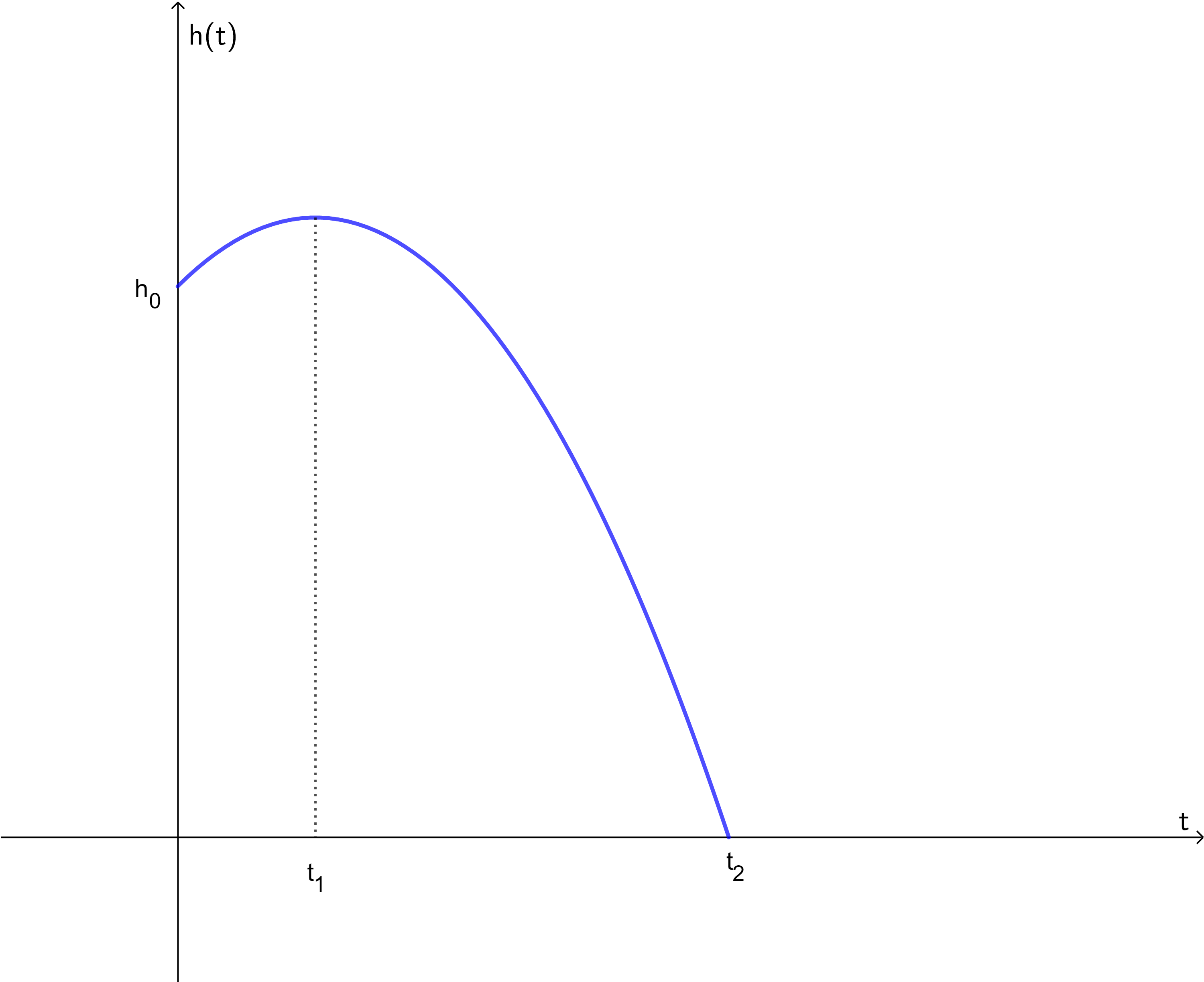
Die Abbildung zeigt das Weg-Zeit-Diagramm eines Körpers, der im Schwerefeld der Erde senkrecht nach oben geworfen wird. Welche Aussagen(n) ist/sind korrekt? 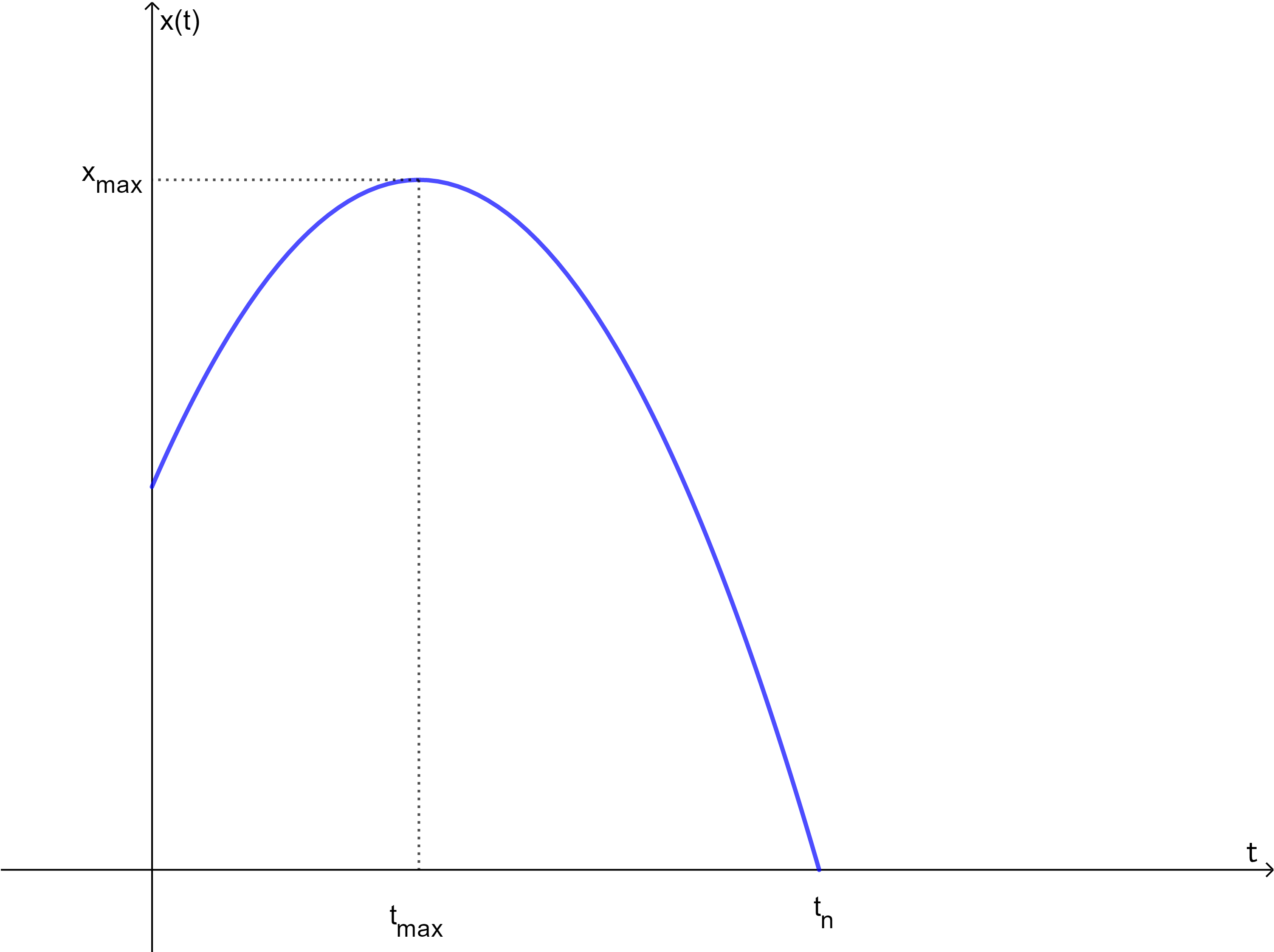 Nr. 4439
|
|
|---|---|
| Lösungsweg | |
|
Anna fährt um \(8\mathrm{\ Uhr}\) mit dem Fahrrad von zu Hause los, um ihre Großmutter zu besuchen. Sie fährt dabei mit einer durchschnittlichen Geschwindigkeit \(v_A=25\ \frac{km}{h}\). Da sie ihr Handy vergessen hat - und das während der Fahrt auch nicht bemerkt - fährt ihr ihr Bruder Leo um \(9\, : \, 30\mathrm{\ Uhr}\) mit dem Auto nach. Er fährt dabei mit einer durchschnittlichen Geschwindkeit von \(v_L=70\ \frac{km}{h}\). Wann hat Leo seine Schwester Anna eingeholt? Nr. 4440
|
|
|---|---|
| Lösungsweg | |
|
Anna fährt um \(17\mathrm{\ Uhr}\) mit dem Moped von zu Hause los, um ihre Großmutter zu besuchen. Sie fährt dabei mit einer durchschnittlichen Geschwindigkeit \(v_A=35\ \frac{km}{h}\). Da sie ihr Handy vergessen hat - und das während der Fahrt auch nicht bemerkt - fährt ihr ihr Bruder Leo um \(17\, : \, 20\mathrm{\ Uhr}\) mit dem Auto nach. Er fährt dabei mit einer durchschnittlichen Geschwindkeit von \(v_L=60\ \frac{km}{h}\). Wie weit entfernt von zu Hause holt Leo seine Schwester Anna ein? Nr. 4441
|
|
|---|---|
| Lösungsweg | |
NEWS
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!