Fragenliste von Impuls, Kräfte und Beschleunigung

Ein Objekt beschleunigt innerhalb von $10$ Sekunden gleichförmig von der Geschwindigkeit $v_0 = 10 \ \frac{m}{s}$ $ auf die Geschwindigkeit $v_1= 60 \ \frac{m}{s}$. Berechne die Beschleunigung $a$ des Objekts. Nr. 1532
	$a=10 \ \frac{m}{s^2}$
	$a=5 \ \frac{m}{s}$
	$a=5 \ \frac{m}{s^2}$
	$a = 50\ \frac{m}{s}$
	$a=6 \ \frac{m}{s^2}$
Lösungsweg $a= \frac{ \Delta v}{\Delta t}= \frac{v_1-v_0}{\Delta t}= \frac{60 \ \frac{m}{s} - 10 \ \frac{m}{s}}{10s}=5 \ \frac{m}{s^2}$

Ein Auto hat die Anfangsgeschwindigkeit $v_0 = 30,0 \ \frac{km}{h}$ und beschleunigt in $20,0$ Sekunden gleichförmig auf die Geschwindigkeit $v_1=50,0 \ \frac{km}{h}$. Berechne die in dieser Zeit zurückgelegte Stecke $s$ (Beschleunigungsstecke). Nr. 1534
	$s=111\ m$
	$s=222\ m$
	$s=333\ km$
	$s=444\ m$
	$s=75\ m$
Lösungsweg Das Auto hat die Beschleunigung $a= \frac{\Delta v}{\Delta t}= \frac{50 \ \frac{km}{h} - 30 \ \frac{km}{h}}{20 \ s}=0,278 \ \frac{m}{s^2}$ Für die zurückgelegte Stecke $s$ gilt $s=v_0 t +\frac{1}{2} a t^2$ und somit $s=30 \ \frac{km}{h} \cdot 20s +\frac{1}{2} \cdot 0,278 \frac{m}{s^2} \cdot (20s)^2=8,33 \frac{m}{s} \cdot 20s +\frac{1}{2} \cdot 0,278 \frac{m}{s^2} \cdot 400s^2$ $ s=222m$

Sie beschleunigen aus dem Stillstand für eine halbe Minute mit der Beschleunigung $a= 2,0 \frac{m}{s^2}$. Wie schnell sind Sie nun? Nr. 1551
	$v= 1,0 \frac{m}{s}$
	$v= 1,0 \frac{km}{h}$
	$v= 60,0 \frac{m}{s}$
	$v= 60,0 \frac{km}{h}$
Lösungsweg $v=a \Delta t = 2,0 \frac{m}{s^2} \cdot 30 s =60 \frac{m}{s}$

Die Geschwindigkeit(sfunktion) $v(t)$ ist die erste Ableitung der Ortsfunktion $x(t)$ nach der Zeit $t$, d.h. $v(t)= \frac{d}{dt} x(t)$. Gegeben sei die Ortsfunktion $x(t)= 4\frac{m}{s^2} t^2 -32 \frac{m}{s} t + 100m$ $, welche ein gleichmäßig beschleunigtes Objekt beschreibt. Bestimme für dieses Beispiel die Geschwindigkeitsfunktion $v(t)$. Nr. 1553
	$v(t)= 4\frac{m}{s^2} t -32 \frac{m}{s} + 100m$
	$v(t)= 4\frac{m}{s^2} t -32 \frac{m}{s} $
	$v(t)= 8\frac{m}{s^2} t -32 \frac{m}{s} $
Lösungsweg Die Funktion $x(t)= 4\frac{m}{s^2} t^2 -32 \frac{m}{s} t + 100m$ $ enthält 3 Terme: Der erste wird durch differenzieren nach $t$ zu $4\cdot2 \frac{m}{s^2}t$, der zweite zu $-32 \frac{m}{s}$, und der letzte verschwindet (weil zeitunabhänig). Somit erhält man insgesamt $v(t)= 8\frac{m}{s^2} t -32 \frac{m}{s} $ $

Beschleunigungen werden oft, anstatt in SI-Einheiten, als Vielfaches der Erdbeschleunigung $g \approx 9,81 \frac{m}{s^2}$ angegeben. Betrachten wir als Beispiel ein Formel-1-Auto. Ein solches Fahrzeug beschleunigt beim Start in ca. 2,0 Sekunden von 0 auf 100 km/h. Die wievielfache Erdbeschleunigung spürt demnach ein Formel-1-Pilot in Fahrtrichtung? Nr. 1603
	$a=3g$
	$a=14g$
	$a=1,4g$
	$a=0,7 g$
Lösungsweg Berechnen wir zunächst die Beschleunigung in SI-Einheiten: $a= \frac{\Delta v}{\Delta t}= \frac{100 \frac{km}{h}}{2,0 s}= \frac{100 \cdot \frac{1000m}{3600s}}{2,0s}=13,9 \frac{m}{s^2}$. Das Verhältnis $a/g$ zur Erdbeschleunigung $g \approx 9,81 \frac{m}{s^2}$ ist also $\frac{a}{g}=1,4$, d.h. $a=1,4 g$ . Der Fahrer wird also mit dem 1,4-fachen seines Körpergewichts in den Sitz gedrückt.

Auf ein Objekt mit Masse $m=3,2 kg$ wirkt eine konstante Kraft von $F=18,0 kN$. Wie groß wird somit die Beschleunigung $a$ des Objekts sein? Nr. 1604
	$a=5,6 \frac{m}{s^2}$
	$a=5,6 \cdot 10^3 \frac{m}{s^2}$
	$a=5,6 \cdot 10^3 \frac{N}{kg}$
	$a=0,2 \frac{m}{s^2}$
	$a=0,2 \cdot 10^{-3} \frac{m}{s^2}$
Lösungsweg Es gilt $F=ma$ und somit $a=\frac{F}{m}=\frac{18,0 \cdot 10^3 N}{3,2kg}=5,6 \cdot 10^3 \frac{N}{kg} $. Ausserdem lässt sich durch $F=ma$ ableiten, dass $\frac{N}{kg}=\frac{m}{s^2}$.

Welche Kraft $F$ ist nötig um ein Objekt mit Masse $m=4,2 kg$ in 5,0 Sekunden von der Geschwindigkeit $v_0=20 \frac{m}{s}$ auf die Geschwindigkeit $40 \frac{m}{s}$ zu beschleunigen? (in SI-Einheit) Nr. 1605
	$F=17N$
	$F=34N$
	$F=17kN$
	$F=34kN$
Lösungsweg Es gilt $F=ma$ wobei $a=\frac{\Delta v}{\Delta t}$ mit $\Delta v= v_1-v_0$. Insgesamt also $F=m \frac{\Delta v} {\Delta t}= 4,2 kg \frac{\left(40 \frac{m}{s}- 20 \frac{m}{s}\right)}{5,0s}=17N$.

Ein Auto ($m=900kg$) benötigt $22s$ um aus dem Stand auf $80\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Beschleinigung? Nr. 1991
	$a=0,57\frac m{s^2}$
	$a=0,92\frac m{s^2}$
	$a=1,01\frac m{s^2}$
	$a=2,27\frac m{s^2}$
	$a=3,64\frac m{s^2}$

Ein Auto ($m=900kg$) benötigt $22s$ um aus dem Stand auf $80\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1992
	$F=737,6N$
	$F=823,5N$
	$F=862,1N$
	$F=909,1N$
	$F=1023,5N$

Ein Auto ($m=900kg$) benötigt $4,6s$ um aus dem Stand auf $100\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Beschleunigung? Nr. 1993
	$a=4,59\frac m{s^2}$
	$a=5,29\frac m{s^2}$
	$a=6,04\frac m{s^2}$
	$a=7,23\frac m{s^2}$
	$a=7,89\frac m{s^2}$

Ein Auto ($m=900kg$) benötigt $4,6s$ um aus dem Stand auf $100\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1994
	$F=5434,8N$
	$F=5827,9N$
	$F=6237,8N$
	$F=6933,4N$
	$F=7293,1N$

Ein Auto ($m=800kg$) benötigt $7,2s$ um aus dem Stand auf $100\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Beschleunigung? Nr. 1995
	$a=0,75\frac m{s^2}$
	$a=1,38\frac m{s^2}$
	$a=3,86\frac m{s^2}$
	$a=7,49\frac m{s^2}$
	$a=10,87\frac m{s^2}$

Ein Auto ($m=800kg$) benötigt $7,2s$ um aus dem Stand auf $100\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1996
	$F=935,4N$
	$F=1329,7N$
	$F=1836,3N$
	$F=3086,4N$
	$F=3253,8N$

Ein Auto ($m=1,2t$) benötigt $7,2s$ um aus dem Stand auf $75\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Beschleunigung? Nr. 1997
	$a=1,87\frac m{s^2}$
	$a=2,89\frac m{s^2}$
	$a=3,79\frac m{s^2}$
	$a=4,23\frac m{s^2}$
	$a=5,83\frac m{s^2}$

Ein Auto ($m=1,2t$) benötigt $7,2s$ um aus dem Stand auf $75\frac{km}h$ zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1998
	$F=2893,3N$
	$F=3252,8N$
	$F=3472,2N$
	$F=3928,3N$
	$F=4293,1N$

Ein Schlitten ($m=100kg$) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft $F=50N$ an, die waagrecht in Fahrtrichtung wirkt. Mit welcher Beschleunigung setzt sich der Schlitten in Bewegung? Nr. 1999
	$a=1,5\frac{m}{s^2}$
	$a=1,2\frac{m}{s^2}$
	$a=1,0\frac{m}{s^2}$
	$a=0,5\frac{m}{s^2}$
	$a=0,2\frac{m}{s^2}$

Ein Schlitten ($m=100kg$) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft $F=50N$ an, die waagrecht in Fahrtrichtung wirkt. Wie groß ist die Geschwindigkeit des Schlittens nach $10s$? Nr. 2000
	$v=2\frac{m}{s}$
	$v=5\frac{m}{s}$
	$v=10\frac{m}{s}$
	$v=15\frac{m}{s}$
	$v=25\frac{m}{s}$

Ein Schlitten ($m=100kg$) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft $F=50N$ an, die waagrecht in Fahrtrichtung wirkt. Welchen Weg hat der Schlitten $10s$ nach dem Stillstand zurückgelegt? Nr. 2001
	$s=0,5m$
	$s=2m$
	$s=5m$
	$s=25m$
	$s=50m$
Lösungsweg Die Kraft $F$ ist folgendermaßen definiert $F=m\cdot a$ Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$ In diesem Beispiel sind $s_0=0$ und $v_0=0$. Somit bleibt einzig $s(t)=a\cdot \frac{t^2}{2}$ übrig. Die Beschleunigung $a$ erhalten, wenn wir die Kraft $F$ nach $a$ umformen: $a=\frac{F}{m}$ Eingesetzt bedeutet das: $s(t)=a\cdot \frac{t^2}{2}=\frac{F}{m}\cdot\frac{t^2}{2}\rightarrow s(10)=\frac{50}{100}\cdot\frac{10^2}{2}=25$. Der Schlitten überwindet nach einer Zeit $t=10\,s$ die Strecke $s(10)=s=25\,m$

Ein Schlitten ($m=250kg$) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft $F=100N$ an, die waagrecht in Fahrtrichtung wirkt. Mit welcher Beschleunigung setzt sich der Schlitten in Bewegung? Nr. 2002
	$a=0,2\frac{m}{s^2}$
	$a=0,4\frac{m}{s^2}$
	$a=1,0\frac{m}{s^2}$
	$a=2,5\frac{m}{s^2}$
	$a=25\frac{m}{s^2}$

Ein Schlitten ($m=250kg$) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft $F=100N$ an, die waagrecht in Fahrtrichtung wirkt. Wie groß ist die Geschwindigkeit des Schlittens nach $10s$? Nr. 2003
	$v=4\frac m s$
	$v=5\frac m s$
	$v=8\frac m s$
	$v=15\frac m s$
	$v=25\frac m s$

Ein Schlitten ($m=250kg$) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft $F=100N$ an, die waagrecht in Fahrtrichtung wirkt. Welchen Weg hat der Schlitten $10s$ nach dem Stillstand zurückgelegt? Nr. 2004
	$s=4m$
	$s=10m$
	$s=16m$
	$s=20m$
	$s=40m$
Lösungsweg Die Kraft $F$ ist folgendermaßen definiert $F=m\cdot a$ Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$ In diesem Beispiel sind $s_0=0$ und $v_0=0$. Somit bleibt einzig $s(t)=a\cdot \frac{t^2}{2}$ übrig. Die Beschleunigung $a$ erhalten wir, wenn wir die Kraft $F$ nach $a$ umformen: $a=\frac{F}{m}$ Eingesetzt bedeutet das: $s(t)=a\cdot \frac{t^2}{2}=\frac{F}{m}\cdot\frac{t^2}{2}\rightarrow s(10)=\frac{100}{250}\cdot\frac{10^2}{2}=20$. Der Schlitten überwindet nach einer Zeit $t=10\,s$ die Strecke $s(10)=s=20\,m$

Ein Radfahrer möchte innnerhalb von $10s$ von $20\frac {km} h$ auf $25\frac {km} h$ beschleunigen. Er wiegt 75kg und sein Rad 12kg. Welche Beschleunigung wird er (durchschnittlich) erfahren? Nr. 2005
	$a=0,14\frac{m}{s^2}$
	$a=0,26\frac{m}{s^2}$
	$a=0,42\frac{m}{s^2}$
	$a=0,50\frac{m}{s^2}$
	$a=0,67\frac{m}{s^2}$

Ein Radfahrer möchte innnerhalb von $10s$ von $20\frac {km} h$ auf $25\frac {km} h$ beschleunigen. Er wiegt 75kg und sein Rad 12kg. Welche Kraft muss er bei konstanter Beschleunigung aufbringen? Nr. 2006
	$F=7,5N$
	$F=8,3N$
	$F=9,9N$
	$F=12,1N$
	$F=14,2N$

Ein Radfahrer möchte innnerhalb von $t=10s$ von $v_1=20\,\frac {km}{ h}$ auf $v_2=25\,\frac {km} {h}$ beschleunigen. Er wiegt $m_P=75\,kg$ und sein Rad $m_R=12\,kg$. Welchen Weg $s$ legt er bei gleichmäßiger Beschleunigung $a$ dabei zurück? Nr. 2007
	$s=15,8m$
	$s=37,2m$
	$s=53,0m$
	$s=62,5m$
	$s=87,4m$
Lösungsweg Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$. Die Beschleunigung $a$ des Radfahrers ist $a=\frac{\Delta v}{\Delta t}$, wo $\Delta v=v_2-v_1$ und $\Delta t=t_2-t_1$. Wir setzen $s_0=0$,$t_1=0$ und $v_0=v_1$, d.h. $s(t)=s_0+v_1 \cdot t+\frac{\Delta v}{\Delta t}\cdot \frac{t^2}{2}$ Die Geschwindigkeitsänderung $\Delta v$ in SI-Einheiten umrechnen $\Delta v=5\,\frac{km}{h}=1,3\bar{8}\,\frac{m}{s}$ und drausfolgend ist $a=0,13\bar{8}\,\frac{m}{s^2}$. Mit $v_1=5, \bar{5}\,\frac{m}{s}$ ist $s(10)=5,\bar{5}\cdot10+0,13\bar{8}\cdot \frac{10^2}{2}=62,5\,m$.

Ein Radfahrer möchte innnerhalb von $15s$ von $20\frac {km} h$ auf $30\frac {km} h$ beschleunigen. Er wiegt 75kg und sein Rad 12kg. Welche (durchschnittliche) Beschleunigung erfährt er dabei? Nr. 2008
	$a=0,12\frac{m}{s^2}$
	$a=0,16\frac{m}{s^2}$
	$a=0,19\frac{m}{s^2}$
	$a=0,24\frac{m}{s^2}$
	$a=0,68\frac{m}{s^2}$

Ein Radfahrer möchte innnerhalb von $15s$ von $20\frac {km} h$ auf $30\frac {km} h$ beschleunigen. Er wiegt 75kg und sein Rad 12kg. Welche Kraft muss er bei gleichförmiger Beschleunigung aufbringen? Nr. 2009
	$F=8,2N$
	$F=12,3N$
	$F=16,1N$
	$F=18,7N$
	$F=21,3N$

Ein Radfahrer möchte innnerhalb von $t=15s$ von $v_1=20\,\frac {km} {h}$ auf $v_2=30\,\frac {km} {h}$ beschleunigen. Er wiegt $m_P=75\,kg$ und sein Rad $m_R=12\,kg$. Welchen Weg legt er dabei bei gleichförmiger Beschleunigung $a$ zurück? Nr. 2010
	$s=26,3m$
	$s=58,3m$
	$s=65,4m$
	$s=88,7m$
	$s=104,2m$
Lösungsweg Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$. Die Beschleunigung $a$ des Radfahrers ist $a=\frac{\Delta v}{\Delta t}$, wo $\Delta v=v_2-v_1$ und $\Delta t=t_2-t_1$. Wir setzen $s_0=0$,$t_1=0$ und $v_0=v_1$, d.h. $s(t)=s_0+v_1 \cdot t+\frac{\Delta v}{\Delta t}\cdot \frac{t^2}{2}$ Die Geschwindigkeitsänderung $\Delta v$ in SI-Einheiten umrechnen $\Delta v=10\,\frac{km}{h}=2,\bar{7}\,\frac{m}{s}$ und drausfolgend ist $a=0,185\,\frac{m}{s^2}$. Mit $v_1=5, \bar{5}\,\frac{m}{s}$ ist $s(10)=5,\bar{5}\cdot15+0,185\cdot \frac{15^2}{2}=104,17\,m$.

Eine Radfahrerin bremst vor einer Kreuzung mit konstanter Bremskraft von $v=25\,\frac{km}{ h}$ bis zum Stillstand. Sie braucht dafür einen Bremsweg von $24m$. Sie wiegt $m_P=65\,kg$ und ihr Rad $m_R=15\,kg$. Wie lange braucht sie für die Vollbremsung? Nr. 2011
	$t=2,7s$
	$t=4,3s$
	$t=5,8s$
	$t=6,9s$
	$t=7,4s$
Lösungsweg Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$. Die Beschleunigung $a$ des Radfahrers ist $a=\frac{\Delta v}{\Delta t}$, wo $\Delta v=v_2-v_1$ und $\Delta t=t_2-t_1$. Mit $v_1=25\,\frac{km}{h}=6,9\bar{4}\,\frac{m}{s}$, $v_2=0\,\frac{m}{s}$, $t_1=0$ und $t_2=t$ mit $t$ ist jener Zeitpunkt an dem die Fahrradfahrerin zum Stillstand kommt und damit am Ende des Bremsweges $s(t)=24$ angekommen ist. Mit $s_0=0$ und $a=\frac{-v_1}{t}$ müssen wir die Gleichung $24=v_1\cdot t-\frac{v_1}{t}\cdot \frac{t^2}{2}=v_1 \cdot t - \frac{v_1}{2}\cdot t=\frac{v_1}{2}\cdot t$ nach $t$ auflösen und erhalten $t=\frac{2\cdot 24\,m}{v_1}=\frac{48\,m}{6,9\bar{4}\frac{m}{s}}=6,912\,s$

Eine Radfahrerin bremst vor einer Kreuzung mit konstanter Bremskraft von $v=25\,\frac{km}{ h}$ bis zum Stillstand. Sie braucht dafür einen Bremsweg von $24m$. Sie wiegt $m_P=65\,kg$ und ihr Rad $m_R=15\,kg$. Welche Beschleunigung $a$ erfährt sie dabei? Nr. 2012
	$a=0,6\frac{m}{s^2}$
	$a=0,8\frac{m}{s^2}$
	$a=1,0\frac{m}{s^2}$
	$a=1,2\frac{m}{s^2}$
	$a=1,4\frac{m}{s^2}$
Lösungsweg Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$. Die Beschleunigung $a$ der Radfahrerin ist $a=\frac{\Delta v}{\Delta t}$, wo $\Delta v=v_2-v_1$ und $\Delta t=t_2-t_1$. Mit $v_1=25\,\frac{km}{h}=6,9\bar{4}\,\frac{m}{s}$, $v_2=0\,\frac{m}{s}$, $t_1=0$ und $t_2=t$ mit $t$ ist jener Zeitpunkt an dem die Fahrradfahrerin zum Stillstand kommt und damit am Ende des Bremsweges $s(t)=24$ angekommen ist. Mit $s_0=0$ und $a=\frac{-v_1}{t}$ müssen wir die Gleichung $24=v_1\cdot t-\frac{v_1}{t}\cdot \frac{t^2}{2}=v_1 \cdot t - \frac{v_1}{2}\cdot t=\frac{v_1}{2}\cdot t$ nach $t$ auflösen und erhalten $t=\frac{2\cdot 24\,m}{v_1}=\frac{48\,m}{6,9\bar{4}\frac{m}{s}}=6,912\,s$. Daraus folgt $a=\frac{-v_1}{t}=\frac{-6.9\bar{4}\frac{m}{s}}{6,912\,s}=1,0047\,\frac{m}{s^2}$.

Eine Radfahrerin bremst vor einer Kreuzung mit konstanter Bremskraft von $v=25\,\frac{km}{ h}$ bis zum Stillstand. Sie braucht dafür einen Bremsweg von $24m$. Sie wiegt $m_P=65\,kg$ und ihr Rad $m_R=15\,kg$. Welche Kraft $F$ wirkt dabei auf die Bremsen? Nr. 2013
	$F=55,3N$
	$F=63,7N$
	$F=72,9N$
	$F=80,4N$
	$F=93,5N$
Lösungsweg Die allgemeine Ortsgleichung $s(t)$ eines Objektes, auf das die Beschleunigung $a$ wirkt,mit dem Anfangsort $s_0$ und der Anfangsgeschwindigkeit $v_0$ lautet $s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}$. Die Beschleunigung $a$ der Radfahrerin ist $a=\frac{\Delta v}{\Delta t}$, wo $\Delta v=v_2-v_1$ und $\Delta t=t_2-t_1$. Mit $v_1=25\,\frac{km}{h}=6,9\bar{4}\,\frac{m}{s}$, $v_2=0\,\frac{m}{s}$, $t_1=0$ und $t_2=t$ mit $t$ ist jener Zeitpunkt an dem die Fahrradfahrerin zum Stillstand kommt und damit am Ende des Bremsweges $s(t)=24$ angekommen ist. Mit $s_0=0$ und $a=\frac{-v_1}{t}$ müssen wir die Gleichung $24=v_1\cdot t-\frac{v_1}{t}\cdot \frac{t^2}{2}=v_1 \cdot t - \frac{v_1}{2}\cdot t=\frac{v_1}{2}\cdot t$ nach $t$ auflösen und erhalten $t=\frac{2\cdot 24\,m}{v_1}=\frac{48\,m}{6,9\bar{4}\frac{m}{s}}=6,912\,s$. Daraus folgt $a=\frac{-v_1}{t}=\frac{-6.9\bar{4}\frac{m}{s}}{6,912\,s}=1,0047\,\frac{m}{s^2}$. Wenn wir in die Formel der Kraft $F=m\cdot a$ für $m=m_P+m_R=65\,kg+15\,kg=80\,kg$ imd die oben errechnete Beschleunigung $a$ einsetzen, erhalten wir $F=80\cdot 1,00469=80,375\,N$.

Ein Auto (4,5m) möchte einen Traktor (4m) überholen, der konstant $35\frac{km} h$ schnell fährt. Zu Beginn des Überholvorgangs sind beide gleich schnell und das Auto hat einen Sicherheitsabstand von 40m zum Traktor. Dann beschleunigt das Auto gleichmäßig mit $3\frac{m}{s^2}$ auf $100\frac{km}h$ und überholt dabei den Traktor. Schließlich reiht es sich mit einem Abstand von 35m wieder vor dem Traktor ein. Welche Strecke legt das Auto von Beginn der Beschleunigung bis zum Einreihen vor dem Traktor zurück? Nr. 2014
	$s=92,4m$
	$s=157,7m$
	$s=194,8m$
	$s=257,2m$
	$s=324,3m$

Gegeben sei die Bewegungsgleichung eines Körpers: $x(t)=9t^3+24t$ Wie groß ist die Beschleunigung zum Zeitpunkt t? Nr. 2039
	$a(t)=18$
	$a(t)=27t^2$
	$a(t)=18t$
	$a(t)=54t$
	$a(t)=54$

Zwei Güterzüge stehen nebeneinander im Bahnhof. Ihre Massen betragen 1800t und 1600t, der Abstand ihrer Schwerpunkte 6m. Wie groß ist ihre gegenseitige Anziehungskraft aufgrund ihrer Massen? Nr. 2064
	$F=0,2N$
	$F=1,4N$
	$F=5,3N$
	$F=18,3N$
	$N=45,7N$

Zwei Güterzüge stehen nebeneinander im Bahnhof. Ihre Massen betragen $m_1=1800\,t$ und $m_2=1600\,t$, der Abstand ihrer Schwerpunkte $6\,m$. Wie groß ist die Beschleunigung, die auf den leichteren Zug in Richtung des schwereren Zuges wirkt? Die Beschleunigung wird durch die Schwerkraft zwischen den beiden Zügen verursacht. Nr. 2065
	$a=2,4\cdot 10^{-5}\frac m{s^2}$
	$a=3,3\cdot 10^{-6}\frac m{s^2}$
	$a=4,1\cdot 10^{-7}\frac m{s^2}$
	$a=5,9\cdot 10^{-7}\frac m{s^2}$
	$a=6,5\cdot 10^{-8}\frac m{s^2}$
Lösungsweg Die Kraft zwischen zwei Objekten aufgrund der Gravitation wird durch dass Newtonsche Graviationsgesetz $F_{G}=G\cdot \frac{m_1\cdot m_2}{r^2}$. $m_1$ und $m_2$ sind die Massen der zwei Objekte, $r$ ist der Abstand der Schwerpunkte der zwei Objekte und $G$ ist die Gravitationskonstante mit dem Wert $G=6,67408 \cdot 10^{-11}\,\frac{m^3}{kg \cdot s^2}$. Die Massen der Schiffe in SI-Einheiten $m_1=1800\,t=1,8\cdot 10^6\,kg$ und $m_2=1600\,t=1,6\cdot 10^6\,kg$. $F_G=6,67408\cdot 10^{-11} \frac{1,8\cdot 10^6\cdot 1,6 \cdot 10^6}{6^2}=5,339\,N$ Diese Kraft kann auch in der Form $F=m\cdot a$ dargestellt werden, d.h. die Kraft $F$ wird durch die Beschleunigung $a=\frac{F}{m}$, die auf das Objekt mit der Masse $m$ wirkt, verursacht. Mit der Masse des leichteren Schiffes $m=m_2$ ist die Beschleunigung $a=\frac{F_G}{m_2}=\frac{5,339\,N}{1,6\cdot 10^6\,kg}=\frac{5,339\,\frac{kg\cdot m}{s^2}}{1,6\cdot 10^6\,kg}=3,337\cdot10^{-6}\,\frac{m}{s^2}$

In einem Hafen steht ein großes Containerschiff ($m_1=400000\,t$) neben einem Schlepper ($m_1=20\,t$). Der Abstand ihrer Schwerpunkte beträgt $35\,m$. Wie groß ist die Schwerkraft die zwischen den beiden Schiffen wirkt? Nr. 2066
	$F=0,003N$
	$F=0,052N$
	$F=0,436N$
	$F=3,827N$
	$F=12,917N$
Lösungsweg Die Kraft zwischen zwei Objekten aufgrund der Gravitation wird durch dass Newtonsche Graviationsgesetz $F_{G}=G\cdot \frac{m_1\cdot m_2}{r^2}$. $m_1$ und $m_2$ sind die Massen der zwei Objekte, $r$ ist der Abstand der Schwerpunkte der zwei Objekte und $G$ ist die Gravitationskonstante mit dem Wert $G=6,67408 \cdot 10^{-11}\,\frac{m^3}{kg \cdot s^2}$. Die Massen der Schiffe in SI-Einheiten $m_1=400\,000\,t=4\cdot 10^{8}\,kg$ und $m_2=20\,t=2\cdot 10^4\,kg$ eingesetzt mit $r=35\,m$ ergibt $F_G=6,67408\cdot 10^{-11} \frac{4\cdot 10^{8}\cdot 2 \cdot 10^4}{35^2}=0,435858\,N$.

In einem Hafen steht ein großes Containerschiff (400.000t) neben einem Schlepper (20t). Der Abstand ihrer Schwerpunkte beträgt 35m. Wie lange braucht der Schlepper um sich nur durch die Anziehungskraft 10cm an das Containerschiff anzunähern? (Sämtliche Reibungen können vernachlässigt werden, das Containerschiff kann als starr angenommen werden. Die Bewegung kann als gleichförmig beschleunigte Bewegung angenommen werden.) Nr. 2067
	$t=96s$
	$t=522s$
	$t=7239s$
	$t=28\ 482s$
	$t=365\ 182s$
Lösungsweg Die Masse des Containerschiffes ist $m_C=400\quad 000\,t=4\times 10^{8}\,kg$ und die Masse des Schleppers ist $m_S=20\,t=2\times 10^4\,kg$. Laut Gravitationsgsetz ist die Kraft zwischen den Schiffen $F=G \frac{m_C\cdot m_S}{r^2}$. Dies lässt sich mit einer Kraft auf den Schlepper $F=m_S \cdot a$ gleichsetzen. Die Beschleunigung $a$ hat dann die folgende Form $a=G \cdot \frac{m_C}{r^2}$. Da das Containerschiff als konstant angesehen wird, betrachten wir die Ortsgleichung des Schleppers $s(t)=s_0+v_0\cdot t+a\cdot\frac{t^2}{2}$. Sowohl der Anfangsort $s_0$ als auch die Anfangsgeschwindigkeit $v_0$ sind beide gleich Null,somit reduziert sich $s(t)$ auf $s(t)=a\cdot \frac{t^2}{2}$. Die Frage, wie lange es dauert, bis der Schlepper sich $10\,cm$ an das Containerschiff angenähert hat, bedeutet zu welchem Zeitpunkt $t$ ist $s(t)=10\,cm=0,1\,m$. Wir formen $s(t)$ nach $t$ um: $t=\sqrt{\frac{2\cdot s(t)}{a}}$. Für $a$ setzen wir $a=G \cdot \frac{m_C}{r^2}=6,674\times 10^{-11} \cdot \frac{4\times 10^8}{35^2}=0.0002179265\,\frac{m}{s^2}$ ein und mit $s(t)=0,1\,m$ ergibt das für $t=95,799\,s$

Impulserhaltung: Ein Ball $(m_1=0,5kg)$ fliegt mit einer Geschwindigkeit von $v=20\frac ms$ in die Arme des lotrecht hochgesprungenen Torwarts $(m_2=75kg)$, der ihn festhält. Mit welcher Geschwindigkeit $\bar{v}$ fliegt der Torwart nach hinten? Nr. 2068
	$\bar{v}=0,05\frac ms$
	$\bar{v}=0,09\frac ms$
	$\bar{v}=0,13\frac ms$
	$\bar{v}=0,19\frac ms$
	$\bar{v}=0,24\frac ms$
Lösungsweg Das Fangen und Festhalten des Balles durch den Torwart entspricht einem inelastischen Stoß. Für diesen gilt allgemein, dass die Summe der Impulse vor $(p_i)$ und nach $(\bar{p}_i)$ dem Stoß muss gleich groß sein. $\sum_i p_i=\sum_i \bar{p}_i$. Für $i=1,2$ bedeutet dass $m_1\cdot v_1 + m_2 \cdot v_2=(m_1 + m_2) \cdot \bar{v}$, wo $\bar{v}$ die Geschwindigkeit beider Objekte nach dem Stoß ist: $\bar{v}=\frac{m_1\cdot v_1 + m_2 \cdot v_2}{m_1+m_2}$. Da die Geschwindigkeit des Torwarts vor dem Stoß $v_2=0$, ist $\bar{v}=\frac{m_1\cdot v_1 }{m_1+m_2}=\frac{0,5 \,kg \cdot 20\,\frac{m}{s} }{0,5\,kg+75\,kg}=\frac{10 \,kg\cdot \frac{m}{s}}{75,5\,kg}=0,132\,\frac{m}{s}$

Welche Kraft F wird benötigt, wenn ein Körper mit der Masse m=12kg in 4 Sekunden von 30 m/s auf 50 m/s beschleunigt? Nr. 3110
	$F=60\,N$
	$F=30\,N$
	$F=70\,N$
	$F=40\,N$
	$F=80\,N$
Lösungsweg $F=m\cdot a$ Die Veränderung der Geschwindigkeit eines Objektes mit der Beschleunigung a von v1 auf v2 $v2-v1=\Delta v=a\cdot t \rightarrow a=\frac{\Delta v}{t}$ und damit berechnet sich die Kraft F wie folgt $F=12\cdot\frac{50-30}{4}=60\,N $

Welche Masse $m $ besitzt ein Körper, auf den die Kraft $F=90\,N$ wirkt, während er in 2 Sekunden von $100\, \frac{km}{h}$ auf $130\, \frac{km}{h}$ beschleunigt wird? Nr. 3111
	$m=23,5\,kg $
	$m=21,6kg$
	$m=21430\,g$
	$m=12,7\,g$
Lösungsweg $F=m\cdot a$ $130 \,\frac{km}{h}=36,1\,\frac{m}{s} \qquad\text{und}\qquad 100\,\frac{km}{h}=27,8\,\frac{m}{s}$ $90=m\cdot\(\frac{36,1-27,8}{2}$ \) $\rightarrow m=21.69\,kg$

Ein Objekt beschleunigt aus dem Stillstand zu einer Geschwindigkeit $v=180\,\frac{km}{h}$ in einer Zeit von $t=4,8\,s$. Wenn es nun mit der selben gleichmäßigen Beschleunigung $a$ für eine Zeit $t=10,5\,s$ beschleunigt, wie gross ist die Momentangeschwindigkeit $v$ des Objektes zu diesem Zeitpunkt? Nr. 3112
	$v=30,38 m/s$
	$v=109,38 \,\frac{m}{s}$
	$v=109,38 \,\frac{km}{h}$
	$v=393,75\,\frac{km}{h}$
Lösungsweg $180\, \frac{km}{h}=50\,\frac{m}{s}$ $a=\frac{\Delta v}{\Delta t}=\(\frac{50-0}{4,8-0}$=10,42m/s^2 \) $\rightarrow \text{nach}\qquad t=10,5\,s \qquad\text{ist}\qquad v=109,38\,\frac{m}{s}=393,75\,\frac{km}{h}$

Ein Auto fährt mit der Geschwindigkeit $v_1=30\,\frac{km}{h}$ und beschleunigt gleichmäßig innerhalb einer Zeit $t=10\,s$ auf $v_2=60\,\frac{km}{h}$. Welche Strecke $s$ hat das Auto während des Beschleunigungvorganges zurückgelegt? Nr. 3113
	$s=112m$
	$s=125m$
	$s=164m$
	$s=131m$
Lösungsweg Umrechung der Einheiten: $v_2=60\,\frac{km}{h}=16,\dot{6}\frac{m}{s}$ und $v_1=30\,\frac{km}{h}=8,\dot{3}\frac{m}{s}$ Die Beschleunigung des Fahrzeugs: $a=\frac{16,\dot{6}-8,\dot{3}}{10}=0,83\frac{m}{s^2}$ Für die Strecke $s$ gilt: $s(t)=s_0+v_0\cdot t+\frac{1}{2} a\cdot t^2$ wo $s_0$ die Anfangsposition ist, in diesem Beispiel $s_0=0$, und $v_0$ ist die Anfangsgeschwindigkeit, die hier $v_0=v_1=30\,\frac{km}{h}$ ist. Das eingesetzt ergibt: $s=125m$

Ein Auto mit einer Masse $m=1,3 \,t$ benötigt ein Zeit $t=5,6\,s$ um aus dem Stillstand auf die Geschwindigkeit $v=100\, \frac{km}{h}$ zu beschleunigen. Wie hoch ist die durchschnittliche Kraft des Motors? Nr. 3114
	$F=5349,3\,N$
	$F=6448,41\,N$
	$F=6247,26\,N$
	$F=5411,98\,N$
Lösungsweg Die Kraft $F=m\cdot a$ ergibt mit den Angaben aus dem Beispiel, wobei die Geschwindigkeit $v=100\,\frac{km}{h}=27,\dot{7}\,\frac{m}{s}$ ist, $F=1300\cdot\(\frac{27,\dot{7}}{5,6}$=6448,41\,N\)

Ein Auto $\left(m=1,2\,t\right)$ braucht $t=6,3\,s$ um von$0-100\,\frac{km}{h}$ zu beschleunigen. Wie hoch ist die durchschnittliche Kraft des Motors? Nr. 3126
	$F=5276,2\,N$
	$F=19,047\,kN$
	$F=5291,01\,N$
	$F=4389,56\,N$
Lösungsweg $F=m\cdot a$ daraus folgt: $F=1200\cdot \frac{27,\dot{7}}{6,3}=5291,01\,N$

Ein Objekt überträgt bei einem elastischen Stoss mit einer Geschwindigkeit $v=30\,\frac{km}{h}$ einen Impuls $p=87366 \,\frac{kg\cdot m}{s}$. Welche Masse $m$ besitzt dieses Objekt? Nr. 3127
	$m=1,052\,t$
	$m=10526\,kg$
	$m=105,26\,kg$
	$m=10,526\,t$
Lösungsweg $p=m\cdot v$ $30\,\frac{km}{h}=8,\dot{3}\,\frac{m}{s}$ umgeformt und eingesetzt: $m=\frac{87366}{8,\dot{3}}=10526\,kg$

Auf ein Objekt, welches aus dem Stand in $t=3,2\,s$ auf $v=60\,\frac{km}{h}$ beschleunigt, wirkt eine konstante Kraft $F=3,4\,kN$. Was ist somit die Masse $m$ des Objekts? Nr. 3128
	$m=0,6528\,t$
	$m=537,5\,kg$
	$m=721,2\,kg$
	$m=398\,kg$
	$m=0,733\,t$
Lösungsweg Die Kraft berechnet sich wie folgt $F=m\cdot a$. Die Geschwindigkeit umgerechnet $v=60\,\frac{km}{h}\rightarrow v=16,\dot{6}\,\frac{m}{s}$. Die Beschleunigung $a=\frac{v}{t}=5.208\dot{3}\,\frac{m}{s^2}$ wird in die folgende Umformung eingesetzt: $m=\frac{F}{a}=652,8\,kg$

Welche Geschwindigkeit $v$ muss ein Objekt mit der Masse $m=370\,kg$ haben um einen Impuls $p=1000\,\frac{kg\cdot m}{s}$ zu erzeugen? Nr. 3129
	$v=2,7\,\frac{m}{s}$
	$v=2,7\,\frac{km}{h}$
	$v=5,4\,\,\frac{m}{s}$
	$v=4,2\,\frac{km}{h}$
Lösungsweg $p=m\cdot v$ umgeformt nach v und eingesetzt: $v=\frac{1000}{370}=2,7\,\frac{m}{s}$

Ein Auto mit einer Masse $m=1,4\,t$ braucht $t=9,8\,s$ um aus dem Stand die finale Geschwindigkeit $v=130\,\frac{km}{h}$ zu erreichen. Welche Kraft muss der Motor durchschnittlich dafür aufbringen? Nr. 3130
	$F=5,158kN$
	$F=515N$
	$F=51587N$
	$F=51,8kN$
Lösungsweg $F=m\cdot a$ Die Geschwindigkeit umgeformt $v=130\,\frac{km}{h}\rightarrow 36.1\,\frac{m}{s}$ $F=1400\cdot \frac{36,1}{9,8}=5158,7N$

Ein Objekt mit der Masse $m=530\,kg$ startet aus dem Stand mit einer gleichmäßigen Beschleunigung $a=4,8\,\frac{m}{s^2}$. Es bewegt sich auf einer geraden Strecke für $t=9,3\,s$ bis es mit einem massiven Hindernis kollidiert. Welchen Impuls $p$ hatte das Objekt zum Zeitpunkt des Aufpralls? Nr. 3131
	$p=62456,3 \,\frac{kg\cdot m}{s}$
	$p=2,36592\cdot 10^4 \,\frac{kg\cdot m}{s}$
	$p=5,351\cdot 10^4 \,\frac{kg\cdot m}{s}$
	$p=58247\,\frac{kg\cdot m}{s}$
Lösungsweg Der Impuls $p=m\cdot v$ berechnet sich mit der Geschwindigkeit $v=a\cdot t$, welche am Ende der Bahn den Wert$v=4,8\cdot 9,3=44,64\,\frac{m}{s}$hat. $\rightarrow p=530\cdot 44,64=23659,2 \,\frac{kg\cdot m}{s}$

Ein massebehafteter Körper $m=400\,kg$ prallt mit $v=70\,\frac{km}{h}$ gegen eine Wand. Wie groß ist der entstandene Impuls $p$? Nr. 3132
	$p=3333,\dot{3} \,\frac{kg\cdot m}{s}$
	$p=4444,\dot{4} \,\frac{kg\cdot m}{s}$
	$p=5555,\dot{5} \,\frac{kg\cdot m}{s}$
	$p=6666,\dot{6}\,\frac{kg\cdot m}{s}$
	$p=7777,\dot{7}\,\frac{kg\cdot m}{s}$
Lösungsweg In die Formel für den Impuls $p=m\cdot v$ eingesetzt ergibt die umgerechnete Geschwindigkeit $v=70\,\,\frac{km}{h}\rightarrow\,v=19,\dot{4}\,\frac{m}{s}$ einen Impuls $p=400\cdot 19,\dot{4}=7777,\dot{7}\,\frac{kg\cdot m}{s}$

Ein Objekt beschleunigt aus dem Stand mit konstanter Beschleunigung $a=3,2\,\frac{m}{s}$ und das für eine Zeit $t=12\,s$. Wie schnell ist das Objekt jetzt? Nr. 3184
	$v=38,4\,\frac{m}{s}$
	$v=138,24\,\frac{km}{h}$
	$v=95,2\,\frac{km}{h}$
	$v=42\,\frac{m}{s}$
Lösungsweg Die Geschwindigkeit ist das Produkt der Beschleunigung und der Zeit $v=a\cdot t$. D.h. $v=3,2\cdot 12=38,4\,\frac{m}{s}$

Der Abstand zwischen zwei Körpern und deren Mittelpunkte beträgt $r=10\,m$. Körper $A$ besitzt eine Masse $m_A=4,5\cdot 10^{6}\,kg$ während Körper $B$ lediglich eine Masse $m_B=10\,kg$ aufweist. Mit welcher Kraft $F$ ziehen sich beide Körper an? Nr. 3188
	$F=0,003N$
	$F=0,0003N$
	$F=0,00003N$
	$F=0,000003N$
Lösungsweg Es gilt das Newtonsche Graviationsgesetz $F=G\cdot \frac{m_A\cdot m_B}{r^2}$. $G$ ist die Graviationskonstante: $G=6,67408\cdot 10^{-11}\frac{m^3}{kg\cdot s^2}$ Alle Werte eingesetzt: $F=6,67408\cdot 10^{-11}\cdot\frac{1\cdot 4,5\cdot10^6}{10^2}=0,00003\,N$

Ein Skateboarder möchte von $v_1=15\,\frac{km}{h}$ auf $v_2=25\,\frac{km}{h}$ beschleunigen und das in einer Zeit $t=5\,s$. Er selbst wiegt $m_E=79\,kg$ und sein Skateboard $m_S=2\,kg$. Wieviel Kraft $F$ muss er durchschnittlich aufbringen? Nr. 3189
	$F=45N$
	$F=34N$
	$F=39N$
	$F=52N$
	$F=48N$
Lösungsweg Zuallererst rechnet man die Geschwindigkeiten in SI-Einheiten um $v_1=15\,\frac{km}{h}=4,1\dot{6}\,\frac{m}{s}$ $v_2=25\,\frac{km}{h}=6,9\dot{4}\,\frac{m}{s}$ Die Kraft $F$ berechnet sich folgendermassen $F=m\cdot a$ mit den eingesetzten Werten und mit $a=\frac{v_2-v_1}{t_2-t_1}$ mit $t_2=t$ und $t_1=0$: $F=81\cdot\frac{6,9\dot{4}-4,1\dot{6}}{5}=45\,N$

Ein Sprinter beschleunigt in $t=9\,s$ aus dem Stand auf $v=5,8\,\frac{m}{s}$. Dabei muss er eine Kraft $F=52\,N$ aufwenden. Wieviel wiegt dieser Sprinter? Nr. 3190
	$m=76,92kg$
	$m=80,67kg$
	$m=85,32kg$
	$m=73,84kg$
	$m=88,38kg$
Lösungsweg Die Kraft ist $F=m\cdot a$ Nach $m$ umgerechnet $m=\frac{F}{a}$ eingesetzt mit $a=\frac{v}{t}$ $m=\frac{52}{\(\frac{5,8}{9}$}=80,67kg\)

Ein Auto mit dem Gesamtgewicht $m=1,3\,t$ beschleunigt von $v_1=50\,\frac{km}{h}$ auf $v_2=100\,\frac{km}{h}$ in einer Zeit $t=4\,s$. Welche Kraft $F$ muss der Motor dafür aufbringen? Nr. 3191
	$F=4717,5N$
	$F=4513,\dot{8}\,N$
	$F=4396N$
	$F=5362,\dot{2}\,N$
Lösungsweg Zuallererst rechnet man die Geschwindigkeiten in SI-Einheiten um $v_1=50\,\frac{km}{h}=13,\dot{8}\,\frac{m}{s}$ $v_2=100\,\frac{km}{h}=27,\dot{7}\,\frac{m}{s}$ Die Kraft $F$ berechnet sich folgendermassen $F=m\cdot a$ mit den eingesetzten Werten und mit $a=\frac{v_2-v_1}{t_2-t_1}$ mit $t_2=t$ und $t_1=0$: $F=1300\cdot\frac{27,7-13,8}{4}=4513,\dot{8}\,N$

Ein Auto $(m=1,2\,t)$ beschleunigt in $t=4,2\,s$ aus dem Stand auf $v=70\,\frac{km}{h}$. Welche (durchschnittliche) Kraft $F$ muss der Motor dabei aufbringen? Nr. 3351
	$F=5,\dot{5}\,kN$
	$F=5555,\dot{5}\,N$
	$F=555,\dot{5}\,N$
	$F=55,\dot{5}\,kN$
Lösungsweg Zuerst die Geschwindigkeit in SI-Einheiten umrechnen $v=70\,\frac{km}{h}=19,\dot{4}\,\frac{m}{s}$ Die Kraft hat die Form $F=m\cdot a$ $F=1200\cdot \(\frac{19,\dot{4}}{4,2}$=5555,\dot{5}\,N\)

EIn Auto $(m=1000\,t)$ beschleunigt innerhalb von $t=3,2\,s$ von $v_1=30\,\frac{km}{h}$ auf $v_2=50\,\frac{km}{h}$. Welche durchschnittliche Kraft $F$ muss der Motor dabei aufbringen? Nr. 3352
	$F=1654,7N$
	$F=1736,11N$
	$F=1922,3$
	$F=1703,4N$
Lösungsweg Zuerst die Geschwindigkeit in SI-Einheiten umrechnen: $v_1=30\,\frac{km}{h}=8,\dot{3}\,\frac{m}{s}$ $v_2=50\,\frac{km}{h}=13,\dot{8}\,\frac{m}{s}$ Die Beschleunigung $a$ ist das Verhältnis zwischen dem Geschwindigkeitsinterval $\Delta v=v_2-v_1$ und dem Zeitinterval $\Delta t= t_2-t_1$, d.h. $a=\frac{\Delta v}{\Delta t }$ und die Kraft $F=m\cdot a$ also $F=1000\cdot\(\frac{13,\dot{8}-8,\dot{3}}{3,2}$=1736,\dot{1}\,N\)

Ein Lkw $(m=8,3\,t)$ beschleunigt innerhalb von $t=11\,s$ aus dem Stand auf $v=11,7\,\frac{m}{s}$. Welche durchschnittliche Kraft $F$ muss der Motor dafür aufbringen? Nr. 3353
	$F=8664,3N$
	$F=8,828kN$
	$F=7,692kN$
	$F=9374,6N$
Lösungsweg Die Kraft ist folgendermaßen definiert $f=m\cdot a$, wobei die Beschleunigung $a$ die Form $a=\frac{v}{t}$ hat. $F=8300\cdot \(\frac{11,7}{11}$=8828,18\,N\)

Ein Objekt mit der Masse $m=68\,kg$ beschleunigt mit $a=3,8\,\frac{m}{s^2}$. Wie hoch ist der Kraftaufwand $F $während dieser Beschleunigung? Nr. 3354
	$F=236,3N$
	$F=311,28N$
	$F=258,4N$
	$F=202,4N$
Lösungsweg Die Kraft ist folgendermaßen definiert $F=m\cdot a$ $F=68\cdot 3,8=258,4\,N$

Ein Auto mit der Masse $m=1,9\,t$ bringt während einer Beschleunigungsphase eine durchschnittliche Kraft $F=9432,66N$ auf. Wie schnell beschleunigt das Auto? Nr. 3355
	$a=5,23\,\frac{m}{s^2}$
	$a=4,96\,\frac{m}{s^2}$
	$a=4,2\,\frac{m}{s^2}$
	$a=3,98\,\frac{m}{s^2}$
Lösungsweg Die Formel für die Kraft $F$ nach $a$ umgeformt: $F=m\cdot a\rightarrow a=\frac{F}{m}$ $a=\frac{9432,66}{1900}=4,96\,\frac{m}{s^2}$

Ein Auto mit dem Gewicht $m=2,3\,t$ beschleunigt in der Zeit $t=5\,s$ aus dem Stand auf die Geschwindigkeit $v=75\,\frac{km}{h}$. Welche durchschnittliche Kraft $F$ muss der Motor dafür aufbringen? Nr. 3356
	$F=9583,3N$
	$F=8966,72N$
	$F=9023,3N$
	$F=8774,6N$
Lösungsweg Die Kraft hat die Form $F=m\cdot a$ Die Geschwindikeit in SI-Einheiten $v=75\,\frac{km}{h}=20,8\dot{3}\,\frac{m}{s}$ $F=2300\cdot\(\frac{20,8\dot{3}}{5}$=9583,33N\)

Der Motor eines Autos bringt durchschnittlich eine Kraft $F=9667,3N$auf eine Beschleunigung $a=4,22\,\frac{m}{s^2}$ durchzuführen. Welche Masse $m$ besitzt das Auto? Nr. 3357
	$m=2,29t$
	$m=3,16t$
	$m=2,93t$
	$m=3,63t$
Lösungsweg Die Kraft $F=m\cdot a$ nach $m$ umgeformt $m=\frac{F}{a}$. $m=\frac{9667,3}{4,22}=2290,83\,kg$

Welche Einheit hat der Impuls $p$? Nr. 3358
	$[p]=kg\cdot s^2$
	$[p]=\frac{kg}{\frac{m}{s^2}}$
	$[p]=\frac{kg\cdot m}{s}$
	$[p]=kg\cdot m$
Lösungsweg Der Impuls $p=m\cdot v$ Die Einheit der Masse $m$ ist: $[m]=\,kg$ Die Einheit der Geschwindigkeit $v$ ist: $[v]=\frac{m}{s}$ Daher ist die Einheit des Impulses: $[p]=[m]\cdot [v]=kg\cdot \frac{m}{s}=\frac{kg\cdot m}{s}$

Welchen Impuls $p$ hat ein ein Objekt, das die Masse $m=400kg$ hat und sich mit einer Geschwindigkeit $v=6,4\,\frac{m}{s}$ fortbewegt? Nr. 3374
	$p=2560\,\frac{kg\cdot m}{s}$
	$p=2130\,\frac{kg\cdot m}{s}$
	$p=2770\,\frac{kg\cdot m}{s}$
	$p=3140\,\frac{kg\cdot m}{s}$
Lösungsweg Der Impuls $p$ ist folgendermaßendefiniert $p=m\cdot v$. Eingesetzt erigibt das für den Impuls des Objektes $p=400\cdot 6,4=2560\,\frac{kg\cdot m}{s}$

Welchen Impuls $p$ hat ein Auto mit dem Gesamtgewicht $m=4,3\,t$, das mit einer Geschwindigkeit $v=80\,\frac{km}{h}$ fährt? Nr. 3486
	$p=94444,4\,\frac{kg\cdot m}{s}$
	$p=96666,7\,\frac{kg\cdot m}{s}$
	$p=95555,6\,\frac{kg\cdot m}{s}$
	$p=97777,8\,\frac{kg\cdot m}{s}$
Lösungsweg Der Impuls $p$ ist folgendermaßen definiert $p=m\cdot v$ Umrechnung in SI-Einheiten: $m=4,3\,t=4300\,kg$ und $v=80\,\frac{km}{h}=22,\dot{2}\,\frac{m}{s}$ Somit ist $p=4300\cdot 22,\dot{2}=95\,555,\dot{5}\,\frac{kg\cdot m}{s}$

Der Körper $A$ mit der Masse $m_1=5,36 \cdot 10^{9}kg$ und der Körper $B$ mit der Masse $m_2=4,49 \cdot 10^{12}kg$ sind durch eine Strecke von $s=2,9 \cdot 10^6$$m$ voneinander entfernt. Mit welcher Kraft $F$ ziehen sie sich gegenseitig an? Nr. 3524
	$F=0,191N$
	$F=191N$
	$F=1,91N$
	$F=19,1N$
Lösungsweg Zur Berechnung der Kraft gilt das Newtonsche Gravitationsgesetzt: $F_1=F_2=G \cdot \(\frac{m_1 \cdot m_2}{r^2}$\) G...Gravitationskonstante $6,67 \cdot 10^{-11} \(\frac{m^3}{kg \cdot s^2}$\)

Die Objekte $A$ mit einer Masse $m=3,51 \cdot 10^6t$ und $B$ mit einer Masse von $m=5,28 \cdot 10^{14}kg$ sind $s=1,024\cdot 10^7m$ voneinander entfernt. Mit welcher Kraft $F$ ziehen sich die beiden Objekte $A$ und $B$ an? Nr. 3525
	$F=1,18N$
	$F=1,49N$
	$F=2,1N$
	$F=0,86N$
Lösungsweg Für die Anziehungskraft zwischen zwei Planeten gilt Newton's Gravitationsgesetz: $F_1=F_2=G \cdot \(\frac{m_1 \cdot m_2}{r^2}$ \) wobei G die Gravitationskonstante mit dem Wert $6,67 \cdot 10^{-11}\frac{m^3}{kg\cdot s^2}$ ist.

Ein anfänglich ruhendes Objekt gleitet reibungslos aus der Höhe $h$ eine Rampe hinunter. Am Ende der Rampe befindet sich eine Schleife mit dem Radius $r = 2m$. Wie groß muss $h$ mindestens sein, damit das Objekt beim Passieren der Schleife nicht von der Schleife fällt? 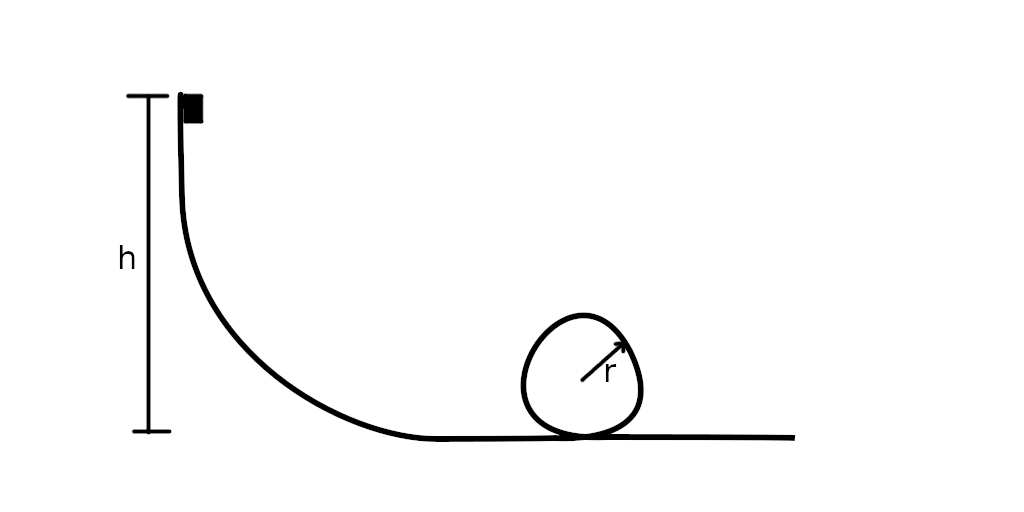Nr. 4065
	$h = 3m$
	$h = 5m$
	$h = 10m$
	$h = 12m$
Lösungsweg Damit das Objekt in der Bahn bleibt, muss die Zentrifugalkraft $F_Z$ mindestens gleich der Schwerkraft $F_g$ sein. Für den höchsten Punkt der Schleife soll also gelten: $\frac{m\cdot v^2}{r} = m\cdot g$ Daraus erhält man die benötigte Geschwindigkeit: $v = \sqrt{g\cdot r}$ Das Objekt hat anfänglich eine potentielle Energie $E_{pot} = m\cdot g\cdot h$. Am höchsten Punkt der Schleife befindet es sich auf einer Höhe von $2\cdot r$, dementsprechend wurde ein Teil seiner Energie in kinetische Energie umgewandelt: $E_{kin} = \frac{m\cdot v^2}{2} = m\cdot g\cdot (h - 2\cdot r)$ Diese gleichung kann man nun nach $h$ auflösen: $h = \frac{v^2}{2\cdot g} + 2\cdot r$ Schließlich kann man den oben erhaltenen Ausdruck für die Geschwindigkeit $v$ in die Formel für die Höhe $h$ einsetzen und erhält: $h = \frac{5}{2}\cdot r$

Gegeben sei eine hypothetische, ringförmige Raumstation. Die Raumstation dreht sich mit einer Winkelgeschwindigkeit von einer Umdrehung pro Stunde, um eine künstliche Schwerkraft für die Besatzung zu erzeugen, welche sich auf der Innenseite des Rings befindet. Wie groß muss der Radius $r$ des Rings sein, um eine Schwerkraft ähnlich der auf der Erdoberfläche zu erzeugen? Nr. 4120
	$r = 5621m$
	$r = 3220km$
	$r = 0,81km$
	$r= 1,057\cdot 10^{10}m$
Lösungsweg Die künstliche Schwerkraft wird durch die Zentrifugalkraft erzeugt, gegeben durch $F_Z = m\om^2r$, mit der Masse $m$ des Objekts, auf dass die Kraft wirkt, dem Radius der Kreisbahn $r$, und der Winkelgeschwindigkeit $\om$, mit der sich das Objekt auf der Kreisbahn bewegt. Diese Kraft soll gleich der Gewichtskraft $F_G = mg$ mit der Schwerebeschleunigung auf der Erde $g = 9,81ms^{-2}$ Setzt man beide Kräfte gleich, kann man auf den Radius umformen: $m\om^2r = mg$ $r = \frac{g}{\om^2}$ Für das Endergebnis benötigen wir die Winkelgeschwindigkeit in SI-Einheiten (rad/s). Eine Umdrehung pro Stunde sind $\om =\frac{ 360^\circ}{ h} = \frac{2\pi \qquad rad}{3600s} = 1,75\cdot 10^{-3} \frac{rad}{s} = 1,75\frac{mrad}{s}$ Einsetzen ergibt für den Radius $r = 3220km$ was ungefähr dem halben Erdradius entspricht. Eine kompaktere Raumstation müsste sich dementsprechend sehr viel schneller drehen.

Berechnen Sie die Beschleunigung $a_G$, die ein Objekt auf der Erdoberfläche durch die Gravitationskraft erfährt. Vergleichen Sie sie mit der entgegengesetzten Beschleunigung $a_Z$ der Zentrifugalkraft, die auf ein Objekt am Äquator wirkt und geben Sie das Verhältnis der beiden Beschleunigungen an. Verwenden Sie für die Berechnungen einen mittleren Erdradius von $R = 6\;378\;137m$ und eine mittlere Dichte der Erde von $\rho = 5518\frac{kg}{m^3}$. Sie können für diese Aufgabe annehmen, dass die Erde eine Kugel ist. Nr. 4121
	$\frac{a_Z}{a_G} = 3,43\cdot 10^{-3}$
	$\frac{a_Z}{a_G} = 8,26\cdot 10^{-2}$
	$\frac{a_Z}{a_G} = 0,12$
	$\frac{a_Z}{a_G} =9,72\cdot 10^{-4}$
Lösungsweg Die Gravitationskraft ist gegeben durch $F_G = G\cdot \frac{m\cdot M}{R^2}$ mit der Masse des Objekts $m$, der Erdenmasse $M$ und der Gravitationskonstante $G = 6,674 \cdot 10^{-11} \frac{m^3}{kg\cdot s^2}$. Die Masse der Erde erhalten wir über das Volumen einer Kugel mit Radius $R$ multipliziert mit der Dichte $\rho$: $M = \frac{4\pi}{3} \cdot R^3 \cdot \rho = 6\cdot10^{24}kg$ Damit ergibt sich für die Beschleunigung $a_G = \frac{F_G}{m} = G\cdot \frac{M}{R^2} = 9,84\frac{m}{s^2}$ Die Zentrifugalkraft ist gegeben durch $F_Z = m\om^2 R$ wobei $R$ der Erdradius ist (da wir uns auf dem Äquator befinden) und $\om$ die Winkelgeschwindigkeit. Wie manche wissen benötigt die Erde für eine Umdrehung einen Tag, damit erhalten wir $\om = 2\pi \qquad \frac{rad}{1d} = 2 \pi \qquad \frac{rad}{86400s} = 7,27\cdot 10^{-5} \frac{rad}{s}$ Für unsere Beschleunigung erhalten wir somit $a_Z = \frac{F_Z}{m} = \om^2R = 3,37\cdot 10^{-2}\frac{m}{s^2}$ Zieht man $a_Z$ von $a_G$ ab erhalten wir den bekannte Wert von $g = 9,81\frac{m}{s^2}$ Das Verhältnis $\frac{a_Z}{a_G} = 3,43\cdot 10^{-3}$ zeigt, dass die Zentrifugalkraft im Vergleich zur Schwerkraft unbedeutend ist.

Vergleichen Sie die die Coulombkraft $F_C$ und die Gravitationskraft $F_G$, die zwischen einem Elektron und einem Proton wirkt. Berechnen Sie das Verhältnis $\frac{F_C}{F_G}$ der beiden Kräfte. Einige hilfreiche Konstanten: Elementarladung $e = 1,6\cdot 10^{-19}C$ Elektronenmasse $m_e = 9,1\cdot10^{-31}kg$ Protonenmasse $m_p = 1,67\cdot10^{-27}kg$ elektrische Feldkonstante $\vareps_0 = 8,85\cdot10^{-12}\frac{As}{Vm}$ Gravitationskonstante $G = 6,67\cdot 10^{-11}\frac{m^3}{kg\cdot s^2}$ Nr. 4140
	$\frac{F_C}{F_G} = 8$
	$\frac{F_C}{F_G} = 2,27\cdot 10^{39}$
	$\frac{F_C}{F_G} = 4,4\cdot 10^{-40}$
	$\frac{F_C}{F_G} = 3,59\cdot 10^{41}$
Lösungsweg Coulombkraft $F_C = \frac{q_e q_p}{4\pi\vareps_0 r^2}$ Gravitationskraft $F_G = G \frac{m_e m_p}{r^2}$ $\frac{F_C}{F_G} = \frac{q_e q_p}{4\pi\vareps_0 r^2} \cdot \left( G \frac{m_e m_p}{r^2}\right)^{-1} = \frac{1}{4\pi\vareps_0G} \cdot \frac{q_e q_p}{m_e m_p} = 2,27\cdot 10^{39}$ Die Gravitationskraft ist demnach in diesem Fall vollkommen vernachlässigbar.

Ein Mann bringe exakt $m = 100 [kg]$ auf die Waage. Die Gewichtskraft, die dabei auf ihn einwirkt, unterscheidet sich je nachdem ob er sich auf der Erd- oder der Mondoberfläche befindet. In welchem Verhältnis stehen beide Kräfte zueinander (Mondmasse: ein Einundachtzigstel der Erdmasse $M_{M}=\frac{M_{E}}{81}$; Mondradius: ca. ein drittel des Erdradius $r_{M}=0,27\cdot r_{E}$)? Nr. 4174
	Die Gewichtskraft auf der der Mondoberfläche ist ca. doppelt so groß wie auf der Erdoberfläche.
	Die Gewichtskraft auf der der Mondoberfläche ist ca. halb so groß wie auf der Erdoberfläche.
	Die Gewichtskraft auf der der Mondoberfläche ist ca. ein Drittel derer auf der Erdoberfläche.
	Die Gewichtskraft auf der der Mondoberfläche ist ca. ein Fünftel derer auf der Erdoberfläche.
	Die Gewichtskraft auf der der Mondoberfläche ist ca. ein Zehntel derer auf der Erdoberfläche.
Lösungsweg Die Gewichtskraft in Radialrichtung lautet $\vec{F}=\frac{GmM}{r^{2}}\vec{e}_{r}$, wobei $\vec{e}_{r}=\frac{\vec{r}}{r}$ der in Radialrichtung weisende Einheitsvektor ist. Der zugehörige richtungsunabhängige skalare Kraftausdruck lautet folglich $F=\sqrt{\vec{F}\vec{F}}=\frac{GmM}{r^{2}}$. Die jeweiligen skalaren Gewichtskräfte auf der Erde und am Mond lauten daher $F_{E}=\frac{GmM_{E}}{r_{E}^{2}}$ und $F_{M}=\frac{GmM_{M}}{r_{M}^{2}}$. Für das Verhältnis der Kräfte gilt folglich $\frac{F_{M}}{F_{E}}=\frac{M_{M}r_{E}^{2}}{M_{E}r_{M}^{2}}=\frac{1}{81\cdot(0,27)^{2}}\approx0,17$. Die Gewichtskraft auf der Mondoberfläche ist folglich etwas geringer als ein Fünftel derer auf der Erdöberfläche.

Gegeben sei eine Walze (Masse $m$, Radius $r$) und eine glatte schiefe Ebene. Wird die Walze schneller, wenn sie $a)$ die Ebene reibungsfrei hinuntergleitet oder $b)$ unter Vernachlässigung von Reibung hinunterrollt?

Hinweis: Das Trägheitsmoment der Walze sei durch $I=\frac{1}{2}mr^{2}$ gegeben.

Nr. 4176

Die Walze ist schneller, wenn sie gleitet.

Die Walze ist schneller, wenn sie rollt.

Lösungsweg

Zwei Kräfte $\vec{F_1} $ und $ \vec{F_2}$, die an einem Körper angreifen, befinden sich im Gleichgewicht, wenn ... Nr. 4597
	der Körper ruht oder sich gleichförmig bewegt.
	der Körper konstant beschleunigt.
	$\vec{F_1}+\vec{F_2}=0$
	$\vec{F_1}=\vec{F_2}$
	der Körper seine Geschwindigkeit ändert.
Lösungsweg Die Gleichgewichtsbedingung (wenn kein Drehmoment wirkt) lautet: $\displaystyle \sum_i \vec{F_i}=0$ Also muss gelten $\vec{F_1}+\vec{F_2}=0$ Es kann, zusätzlich zum Kräftegleichgewicht, aber auch ein Drehmoment wirken. Es muss nicht sein, dass wenn die Kräfte, die auf einen Körper wirken, sich im Gleichgewicht befinden, auch ein Momentengleichgewicht vorliegt. Diese beiden (Kräftegleichgewicht sowie Momentengleichgewicht) sind also gesondert voneinander zu betrachten! Wenn die resultierende Gesamtkraft 0 ist, dann kann der Körper wegen $F=m \cdot a$ nicht beschleunigen. Daher muss er im Zustand der Ruhe oder der gleichförmigen Bewegung sein.

Anmelden

Passwort vergessen
Registrieren

NEWS

Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.

Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support

Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!

https://www.technikum-wien.at/mathe-support/

Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.

Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.

Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.

Anmeldung und Informationen
Warm-up-Kurse

Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!

weitere News

Ein Objekt beschleunigt innerhalb von \(10\) Sekunden gleichförmig von der Geschwindigkeit \(v_0 = 10 \ \frac{m}{s}$ \) auf die Geschwindigkeit \(v_1= 60 \ \frac{m}{s}\). Berechne die Beschleunigung \(a\) des Objekts. Nr. 1532
	\(a=10 \ \frac{m}{s^2}\)
	\(a=5 \ \frac{m}{s}\)
	\(a=5 \ \frac{m}{s^2}\)
	\(a = 50\ \frac{m}{s}\)
	\(a=6 \ \frac{m}{s^2}\)
Lösungsweg \(a= \frac{ \Delta v}{\Delta t}= \frac{v_1-v_0}{\Delta t}= \frac{60 \ \frac{m}{s} - 10 \ \frac{m}{s}}{10s}=5 \ \frac{m}{s^2}\)

Ein Auto hat die Anfangsgeschwindigkeit \(v_0 = 30,0 \ \frac{km}{h}\) und beschleunigt in \(20,0\) Sekunden gleichförmig auf die Geschwindigkeit \(v_1=50,0 \ \frac{km}{h}\). Berechne die in dieser Zeit zurückgelegte Stecke \(s\) (Beschleunigungsstecke). Nr. 1534
	\(s=111\ m\)
	\(s=222\ m\)
	\(s=333\ km\)
	\(s=444\ m\)
	\(s=75\ m\)
Lösungsweg Das Auto hat die Beschleunigung \(a= \frac{\Delta v}{\Delta t}= \frac{50 \ \frac{km}{h} - 30 \ \frac{km}{h}}{20 \ s}=0,278 \ \frac{m}{s^2}\) Für die zurückgelegte Stecke \(s\) gilt \(s=v_0 t +\frac{1}{2} a t^2\) und somit \(s=30 \ \frac{km}{h} \cdot 20s +\frac{1}{2} \cdot 0,278 \frac{m}{s^2} \cdot (20s)^2=8,33 \frac{m}{s} \cdot 20s +\frac{1}{2} \cdot 0,278 \frac{m}{s^2} \cdot 400s^2\) \( s=222m\)

Sie beschleunigen aus dem Stillstand für eine halbe Minute mit der Beschleunigung \(a= 2,0 \frac{m}{s^2}\). Wie schnell sind Sie nun? Nr. 1551
	\(v= 1,0 \frac{m}{s}\)
	\(v= 1,0 \frac{km}{h}\)
	\(v= 60,0 \frac{m}{s}\)
	\(v= 60,0 \frac{km}{h}\)
Lösungsweg \(v=a \Delta t = 2,0 \frac{m}{s^2} \cdot 30 s =60 \frac{m}{s}\)

Die Geschwindigkeit(sfunktion) \(v(t)\) ist die erste Ableitung der Ortsfunktion \(x(t)\) nach der Zeit \(t\), d.h. \(v(t)= \frac{d}{dt} x(t)\). Gegeben sei die Ortsfunktion \(x(t)= 4\frac{m}{s^2} t^2 -32 \frac{m}{s} t + 100m$ \), welche ein gleichmäßig beschleunigtes Objekt beschreibt. Bestimme für dieses Beispiel die Geschwindigkeitsfunktion \(v(t)\). Nr. 1553
	\(v(t)= 4\frac{m}{s^2} t -32 \frac{m}{s} + 100m\)
	\(v(t)= 4\frac{m}{s^2} t -32 \frac{m}{s} \)
	\(v(t)= 8\frac{m}{s^2} t -32 \frac{m}{s} \)
Lösungsweg Die Funktion \(x(t)= 4\frac{m}{s^2} t^2 -32 \frac{m}{s} t + 100m$ \) enthält 3 Terme: Der erste wird durch differenzieren nach \(t\) zu \(4\cdot2 \frac{m}{s^2}t\), der zweite zu \(-32 \frac{m}{s}\), und der letzte verschwindet (weil zeitunabhänig). Somit erhält man insgesamt \(v(t)= 8\frac{m}{s^2} t -32 \frac{m}{s} $ \)

Beschleunigungen werden oft, anstatt in SI-Einheiten, als Vielfaches der Erdbeschleunigung \(g \approx 9,81 \frac{m}{s^2}\) angegeben. Betrachten wir als Beispiel ein Formel-1-Auto. Ein solches Fahrzeug beschleunigt beim Start in ca. 2,0 Sekunden von 0 auf 100 km/h. Die wievielfache Erdbeschleunigung spürt demnach ein Formel-1-Pilot in Fahrtrichtung? Nr. 1603
	\(a=3g\)
	\(a=14g\)
	\(a=1,4g\)
	\(a=0,7 g\)
Lösungsweg Berechnen wir zunächst die Beschleunigung in SI-Einheiten: \(a= \frac{\Delta v}{\Delta t}= \frac{100 \frac{km}{h}}{2,0 s}= \frac{100 \cdot \frac{1000m}{3600s}}{2,0s}=13,9 \frac{m}{s^2}\). Das Verhältnis \(a/g\) zur Erdbeschleunigung \(g \approx 9,81 \frac{m}{s^2}\) ist also \(\frac{a}{g}=1,4\), d.h. \(a=1,4 g\) . Der Fahrer wird also mit dem 1,4-fachen seines Körpergewichts in den Sitz gedrückt.

Auf ein Objekt mit Masse \(m=3,2 kg\) wirkt eine konstante Kraft von \(F=18,0 kN\). Wie groß wird somit die Beschleunigung \(a\) des Objekts sein? Nr. 1604
	\(a=5,6 \frac{m}{s^2}\)
	\(a=5,6 \cdot 10^3 \frac{m}{s^2}\)
	\(a=5,6 \cdot 10^3 \frac{N}{kg}\)
	\(a=0,2 \frac{m}{s^2}\)
	\(a=0,2 \cdot 10^{-3} \frac{m}{s^2}\)
Lösungsweg Es gilt \(F=ma\) und somit \(a=\frac{F}{m}=\frac{18,0 \cdot 10^3 N}{3,2kg}=5,6 \cdot 10^3 \frac{N}{kg} \). Ausserdem lässt sich durch \(F=ma\) ableiten, dass \(\frac{N}{kg}=\frac{m}{s^2}\).

Welche Kraft \(F\) ist nötig um ein Objekt mit Masse \(m=4,2 kg\) in 5,0 Sekunden von der Geschwindigkeit \(v_0=20 \frac{m}{s}\) auf die Geschwindigkeit \(40 \frac{m}{s}\) zu beschleunigen? (in SI-Einheit) Nr. 1605
	\(F=17N\)
	\(F=34N\)
	\(F=17kN\)
	\(F=34kN\)
Lösungsweg Es gilt \(F=ma\) wobei \(a=\frac{\Delta v}{\Delta t}\) mit \(\Delta v= v_1-v_0\). Insgesamt also \(F=m \frac{\Delta v} {\Delta t}= 4,2 kg \frac{\left(40 \frac{m}{s}- 20 \frac{m}{s}\right)}{5,0s}=17N\).

Ein Auto (\(m=900kg\)) benötigt \(22s\) um aus dem Stand auf \(80\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Beschleinigung? Nr. 1991
	\(a=0,57\frac m{s^2}\)
	\(a=0,92\frac m{s^2}\)
	\(a=1,01\frac m{s^2}\)
	\(a=2,27\frac m{s^2}\)
	\(a=3,64\frac m{s^2}\)

Ein Auto (\(m=900kg\)) benötigt \(22s\) um aus dem Stand auf \(80\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1992
	\(F=737,6N\)
	\(F=823,5N\)
	\(F=862,1N\)
	\(F=909,1N\)
	\(F=1023,5N\)

Ein Auto (\(m=900kg\)) benötigt \(4,6s\) um aus dem Stand auf \(100\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Beschleunigung? Nr. 1993
	\(a=4,59\frac m{s^2}\)
	\(a=5,29\frac m{s^2}\)
	\(a=6,04\frac m{s^2}\)
	\(a=7,23\frac m{s^2}\)
	\(a=7,89\frac m{s^2}\)

Ein Auto (\(m=900kg\)) benötigt \(4,6s\) um aus dem Stand auf \(100\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1994
	\(F=5434,8N\)
	\(F=5827,9N\)
	\(F=6237,8N\)
	\(F=6933,4N\)
	\(F=7293,1N\)

Ein Auto (\(m=800kg\)) benötigt \(7,2s\) um aus dem Stand auf \(100\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Beschleunigung? Nr. 1995
	\(a=0,75\frac m{s^2}\)
	\(a=1,38\frac m{s^2}\)
	\(a=3,86\frac m{s^2}\)
	\(a=7,49\frac m{s^2}\)
	\(a=10,87\frac m{s^2}\)

Ein Auto (\(m=800kg\)) benötigt \(7,2s\) um aus dem Stand auf \(100\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1996
	\(F=935,4N\)
	\(F=1329,7N\)
	\(F=1836,3N\)
	\(F=3086,4N\)
	\(F=3253,8N\)

Ein Auto (\(m=1,2t\)) benötigt \(7,2s\) um aus dem Stand auf \(75\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Beschleunigung? Nr. 1997
	\(a=1,87\frac m{s^2}\)
	\(a=2,89\frac m{s^2}\)
	\(a=3,79\frac m{s^2}\)
	\(a=4,23\frac m{s^2}\)
	\(a=5,83\frac m{s^2}\)

Ein Auto (\(m=1,2t\)) benötigt \(7,2s\) um aus dem Stand auf \(75\frac{km}h\) zu kommen. Wie groß ist die durchschnittliche Kraft des Motors? Nr. 1998
	\(F=2893,3N\)
	\(F=3252,8N\)
	\(F=3472,2N\)
	\(F=3928,3N\)
	\(F=4293,1N\)

Ein Schlitten (\(m=100kg\)) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft \(F=50N\) an, die waagrecht in Fahrtrichtung wirkt. Mit welcher Beschleunigung setzt sich der Schlitten in Bewegung? Nr. 1999
	\(a=1,5\frac{m}{s^2}\)
	\(a=1,2\frac{m}{s^2}\)
	\(a=1,0\frac{m}{s^2}\)
	\(a=0,5\frac{m}{s^2}\)
	\(a=0,2\frac{m}{s^2}\)

Ein Schlitten (\(m=100kg\)) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft \(F=50N\) an, die waagrecht in Fahrtrichtung wirkt. Wie groß ist die Geschwindigkeit des Schlittens nach \(10s\)? Nr. 2000
	\(v=2\frac{m}{s}\)
	\(v=5\frac{m}{s}\)
	\(v=10\frac{m}{s}\)
	\(v=15\frac{m}{s}\)
	\(v=25\frac{m}{s}\)

Ein Schlitten (\(m=100kg\)) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft \(F=50N\) an, die waagrecht in Fahrtrichtung wirkt. Welchen Weg hat der Schlitten \(10s\) nach dem Stillstand zurückgelegt? Nr. 2001
	\(s=0,5m\)
	\(s=2m\)
	\(s=5m\)
	\(s=25m\)
	\(s=50m\)
Lösungsweg Die Kraft \(F\) ist folgendermaßen definiert \(F=m\cdot a\) Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\) In diesem Beispiel sind \(s_0=0\) und \(v_0=0\). Somit bleibt einzig \(s(t)=a\cdot \frac{t^2}{2}\) übrig. Die Beschleunigung \(a\) erhalten, wenn wir die Kraft \(F\) nach \(a\) umformen: \(a=\frac{F}{m}\) Eingesetzt bedeutet das: \(s(t)=a\cdot \frac{t^2}{2}=\frac{F}{m}\cdot\frac{t^2}{2}\rightarrow s(10)=\frac{50}{100}\cdot\frac{10^2}{2}=25\). Der Schlitten überwindet nach einer Zeit \(t=10\,s\) die Strecke \(s(10)=s=25\,m\)

Ein Schlitten (\(m=250kg\)) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft \(F=100N\) an, die waagrecht in Fahrtrichtung wirkt. Mit welcher Beschleunigung setzt sich der Schlitten in Bewegung? Nr. 2002
	\(a=0,2\frac{m}{s^2}\)
	\(a=0,4\frac{m}{s^2}\)
	\(a=1,0\frac{m}{s^2}\)
	\(a=2,5\frac{m}{s^2}\)
	\(a=25\frac{m}{s^2}\)

Ein Schlitten (\(m=250kg\)) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft \(F=100N\) an, die waagrecht in Fahrtrichtung wirkt. Wie groß ist die Geschwindigkeit des Schlittens nach \(10s\)? Nr. 2003
	\(v=4\frac m s\)
	\(v=5\frac m s\)
	\(v=8\frac m s\)
	\(v=15\frac m s\)
	\(v=25\frac m s\)

Ein Schlitten (\(m=250kg\)) lässt sich auf einer waagrechten Eisfläche reibungslos verschieben. Am Schlitten greift die Zugkraft \(F=100N\) an, die waagrecht in Fahrtrichtung wirkt. Welchen Weg hat der Schlitten \(10s\) nach dem Stillstand zurückgelegt? Nr. 2004
	\(s=4m\)
	\(s=10m\)
	\(s=16m\)
	\(s=20m\)
	\(s=40m\)
Lösungsweg Die Kraft \(F\) ist folgendermaßen definiert \(F=m\cdot a\) Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\) In diesem Beispiel sind \(s_0=0\) und \(v_0=0\). Somit bleibt einzig \(s(t)=a\cdot \frac{t^2}{2}\) übrig. Die Beschleunigung \(a\) erhalten wir, wenn wir die Kraft \(F\) nach \(a\) umformen: \(a=\frac{F}{m}\) Eingesetzt bedeutet das: \(s(t)=a\cdot \frac{t^2}{2}=\frac{F}{m}\cdot\frac{t^2}{2}\rightarrow s(10)=\frac{100}{250}\cdot\frac{10^2}{2}=20\). Der Schlitten überwindet nach einer Zeit \(t=10\,s\) die Strecke \(s(10)=s=20\,m\)

Ein Radfahrer möchte innnerhalb von \(10s\) von \(20\frac {km} h\) auf \(25\frac {km} h\) beschleunigen. Er wiegt 75kg und sein Rad 12kg. Welche Beschleunigung wird er (durchschnittlich) erfahren? Nr. 2005
	\(a=0,14\frac{m}{s^2}\)
	\(a=0,26\frac{m}{s^2}\)
	\(a=0,42\frac{m}{s^2}\)
	\(a=0,50\frac{m}{s^2}\)
	\(a=0,67\frac{m}{s^2}\)

Ein Radfahrer möchte innnerhalb von \(t=10s\) von \(v_1=20\,\frac {km}{ h}\) auf \(v_2=25\,\frac {km} {h}\) beschleunigen. Er wiegt \(m_P=75\,kg\) und sein Rad \(m_R=12\,kg\). Welchen Weg \(s\) legt er bei gleichmäßiger Beschleunigung \(a\) dabei zurück? Nr. 2007
	\(s=15,8m\)
	\(s=37,2m\)
	\(s=53,0m\)
	\(s=62,5m\)
	\(s=87,4m\)
Lösungsweg Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\). Die Beschleunigung \(a\) des Radfahrers ist \(a=\frac{\Delta v}{\Delta t}\), wo \(\Delta v=v_2-v_1\) und \(\Delta t=t_2-t_1\). Wir setzen \(s_0=0\),\(t_1=0\) und \(v_0=v_1\), d.h. \(s(t)=s_0+v_1 \cdot t+\frac{\Delta v}{\Delta t}\cdot \frac{t^2}{2}\) Die Geschwindigkeitsänderung \(\Delta v\) in SI-Einheiten umrechnen \(\Delta v=5\,\frac{km}{h}=1,3\bar{8}\,\frac{m}{s}\) und drausfolgend ist \(a=0,13\bar{8}\,\frac{m}{s^2}\). Mit \(v_1=5, \bar{5}\,\frac{m}{s}\) ist \(s(10)=5,\bar{5}\cdot10+0,13\bar{8}\cdot \frac{10^2}{2}=62,5\,m\).

Ein Radfahrer möchte innnerhalb von \(15s\) von \(20\frac {km} h\) auf \(30\frac {km} h\) beschleunigen. Er wiegt 75kg und sein Rad 12kg. Welche (durchschnittliche) Beschleunigung erfährt er dabei? Nr. 2008
	\(a=0,12\frac{m}{s^2}\)
	\(a=0,16\frac{m}{s^2}\)
	\(a=0,19\frac{m}{s^2}\)
	\(a=0,24\frac{m}{s^2}\)
	\(a=0,68\frac{m}{s^2}\)

Ein Radfahrer möchte innnerhalb von \(t=15s\) von \(v_1=20\,\frac {km} {h}\) auf \(v_2=30\,\frac {km} {h}\) beschleunigen. Er wiegt \(m_P=75\,kg\) und sein Rad \(m_R=12\,kg\). Welchen Weg legt er dabei bei gleichförmiger Beschleunigung \(a\) zurück? Nr. 2010
	\(s=26,3m\)
	\(s=58,3m\)
	\(s=65,4m\)
	\(s=88,7m\)
	\(s=104,2m\)
Lösungsweg Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\). Die Beschleunigung \(a\) des Radfahrers ist \(a=\frac{\Delta v}{\Delta t}\), wo \(\Delta v=v_2-v_1\) und \(\Delta t=t_2-t_1\). Wir setzen \(s_0=0\),\(t_1=0\) und \(v_0=v_1\), d.h. \(s(t)=s_0+v_1 \cdot t+\frac{\Delta v}{\Delta t}\cdot \frac{t^2}{2}\) Die Geschwindigkeitsänderung \(\Delta v\) in SI-Einheiten umrechnen \(\Delta v=10\,\frac{km}{h}=2,\bar{7}\,\frac{m}{s}\) und drausfolgend ist \(a=0,185\,\frac{m}{s^2}\). Mit \(v_1=5, \bar{5}\,\frac{m}{s}\) ist \(s(10)=5,\bar{5}\cdot15+0,185\cdot \frac{15^2}{2}=104,17\,m\).

Physik Übungsplattform

Fragenliste von Impuls, Kräfte und Beschleunigung

Anmelden

NEWS

Eine Radfahrerin bremst vor einer Kreuzung mit konstanter Bremskraft von \(v=25\,\frac{km}{ h}\) bis zum Stillstand. Sie braucht dafür einen Bremsweg von \(24m\). Sie wiegt \(m_P=65\,kg\) und ihr Rad \(m_R=15\,kg\). Wie lange braucht sie für die Vollbremsung? Nr. 2011
	\(t=2,7s\)
	\(t=4,3s\)
	\(t=5,8s\)
	\(t=6,9s\)
	\(t=7,4s\)
Lösungsweg Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\). Die Beschleunigung \(a\) des Radfahrers ist \(a=\frac{\Delta v}{\Delta t}\), wo \(\Delta v=v_2-v_1\) und \(\Delta t=t_2-t_1\). Mit \(v_1=25\,\frac{km}{h}=6,9\bar{4}\,\frac{m}{s}\), \(v_2=0\,\frac{m}{s}\), \(t_1=0\) und \(t_2=t\) mit \(t\) ist jener Zeitpunkt an dem die Fahrradfahrerin zum Stillstand kommt und damit am Ende des Bremsweges \(s(t)=24\) angekommen ist. Mit \(s_0=0\) und \(a=\frac{-v_1}{t}\) müssen wir die Gleichung \(24=v_1\cdot t-\frac{v_1}{t}\cdot \frac{t^2}{2}=v_1 \cdot t - \frac{v_1}{2}\cdot t=\frac{v_1}{2}\cdot t\) nach \(t\) auflösen und erhalten \(t=\frac{2\cdot 24\,m}{v_1}=\frac{48\,m}{6,9\bar{4}\frac{m}{s}}=6,912\,s\)

Eine Radfahrerin bremst vor einer Kreuzung mit konstanter Bremskraft von \(v=25\,\frac{km}{ h}\) bis zum Stillstand. Sie braucht dafür einen Bremsweg von \(24m\). Sie wiegt \(m_P=65\,kg\) und ihr Rad \(m_R=15\,kg\). Welche Beschleunigung \(a\) erfährt sie dabei? Nr. 2012
	\(a=0,6\frac{m}{s^2}\)
	\(a=0,8\frac{m}{s^2}\)
	\(a=1,0\frac{m}{s^2}\)
	\(a=1,2\frac{m}{s^2}\)
	\(a=1,4\frac{m}{s^2}\)
Lösungsweg Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\). Die Beschleunigung \(a\) der Radfahrerin ist \(a=\frac{\Delta v}{\Delta t}\), wo \(\Delta v=v_2-v_1\) und \(\Delta t=t_2-t_1\). Mit \(v_1=25\,\frac{km}{h}=6,9\bar{4}\,\frac{m}{s}\), \(v_2=0\,\frac{m}{s}\), \(t_1=0\) und \(t_2=t\) mit \(t\) ist jener Zeitpunkt an dem die Fahrradfahrerin zum Stillstand kommt und damit am Ende des Bremsweges \(s(t)=24\) angekommen ist. Mit \(s_0=0\) und \(a=\frac{-v_1}{t}\) müssen wir die Gleichung \(24=v_1\cdot t-\frac{v_1}{t}\cdot \frac{t^2}{2}=v_1 \cdot t - \frac{v_1}{2}\cdot t=\frac{v_1}{2}\cdot t\) nach \(t\) auflösen und erhalten \(t=\frac{2\cdot 24\,m}{v_1}=\frac{48\,m}{6,9\bar{4}\frac{m}{s}}=6,912\,s\). Daraus folgt \(a=\frac{-v_1}{t}=\frac{-6.9\bar{4}\frac{m}{s}}{6,912\,s}=1,0047\,\frac{m}{s^2}\).

Eine Radfahrerin bremst vor einer Kreuzung mit konstanter Bremskraft von \(v=25\,\frac{km}{ h}\) bis zum Stillstand. Sie braucht dafür einen Bremsweg von \(24m\). Sie wiegt \(m_P=65\,kg\) und ihr Rad \(m_R=15\,kg\). Welche Kraft \(F\) wirkt dabei auf die Bremsen? Nr. 2013
	\(F=55,3N\)
	\(F=63,7N\)
	\(F=72,9N\)
	\(F=80,4N\)
	\(F=93,5N\)
Lösungsweg Die allgemeine Ortsgleichung \(s(t)\) eines Objektes, auf das die Beschleunigung \(a\) wirkt,mit dem Anfangsort \(s_0\) und der Anfangsgeschwindigkeit \(v_0\) lautet \(s(t)=s_0+v_0 \cdot t+a\cdot \frac{t^2}{2}\). Die Beschleunigung \(a\) der Radfahrerin ist \(a=\frac{\Delta v}{\Delta t}\), wo \(\Delta v=v_2-v_1\) und \(\Delta t=t_2-t_1\). Mit \(v_1=25\,\frac{km}{h}=6,9\bar{4}\,\frac{m}{s}\), \(v_2=0\,\frac{m}{s}\), \(t_1=0\) und \(t_2=t\) mit \(t\) ist jener Zeitpunkt an dem die Fahrradfahrerin zum Stillstand kommt und damit am Ende des Bremsweges \(s(t)=24\) angekommen ist. Mit \(s_0=0\) und \(a=\frac{-v_1}{t}\) müssen wir die Gleichung \(24=v_1\cdot t-\frac{v_1}{t}\cdot \frac{t^2}{2}=v_1 \cdot t - \frac{v_1}{2}\cdot t=\frac{v_1}{2}\cdot t\) nach \(t\) auflösen und erhalten \(t=\frac{2\cdot 24\,m}{v_1}=\frac{48\,m}{6,9\bar{4}\frac{m}{s}}=6,912\,s\). Daraus folgt \(a=\frac{-v_1}{t}=\frac{-6.9\bar{4}\frac{m}{s}}{6,912\,s}=1,0047\,\frac{m}{s^2}\). Wenn wir in die Formel der Kraft \(F=m\cdot a\) für \(m=m_P+m_R=65\,kg+15\,kg=80\,kg\) imd die oben errechnete Beschleunigung \(a\) einsetzen, erhalten wir \(F=80\cdot 1,00469=80,375\,N\).

Gegeben sei die Bewegungsgleichung eines Körpers: \(x(t)=9t^3+24t\) Wie groß ist die Beschleunigung zum Zeitpunkt t? Nr. 2039
	\(a(t)=18\)
	\(a(t)=27t^2\)
	\(a(t)=18t\)
	\(a(t)=54t\)
	\(a(t)=54\)

Zwei Güterzüge stehen nebeneinander im Bahnhof. Ihre Massen betragen \(m_1=1800\,t\) und \(m_2=1600\,t\), der Abstand ihrer Schwerpunkte \(6\,m\). Wie groß ist die Beschleunigung, die auf den leichteren Zug in Richtung des schwereren Zuges wirkt? Die Beschleunigung wird durch die Schwerkraft zwischen den beiden Zügen verursacht. Nr. 2065
	\(a=2,4\cdot 10^{-5}\frac m{s^2}\)
	\(a=3,3\cdot 10^{-6}\frac m{s^2}\)
	\(a=4,1\cdot 10^{-7}\frac m{s^2}\)
	\(a=5,9\cdot 10^{-7}\frac m{s^2}\)
	\(a=6,5\cdot 10^{-8}\frac m{s^2}\)
Lösungsweg Die Kraft zwischen zwei Objekten aufgrund der Gravitation wird durch dass Newtonsche Graviationsgesetz \(F_{G}=G\cdot \frac{m_1\cdot m_2}{r^2}\). \(m_1\) und \(m_2\) sind die Massen der zwei Objekte, \(r\) ist der Abstand der Schwerpunkte der zwei Objekte und \(G\) ist die Gravitationskonstante mit dem Wert \(G=6,67408 \cdot 10^{-11}\,\frac{m^3}{kg \cdot s^2}\). Die Massen der Schiffe in SI-Einheiten \(m_1=1800\,t=1,8\cdot 10^6\,kg\) und \(m_2=1600\,t=1,6\cdot 10^6\,kg\). \(F_G=6,67408\cdot 10^{-11} \frac{1,8\cdot 10^6\cdot 1,6 \cdot 10^6}{6^2}=5,339\,N\) Diese Kraft kann auch in der Form \(F=m\cdot a\) dargestellt werden, d.h. die Kraft \(F\) wird durch die Beschleunigung \(a=\frac{F}{m}\), die auf das Objekt mit der Masse \(m\) wirkt, verursacht. Mit der Masse des leichteren Schiffes \(m=m_2\) ist die Beschleunigung \(a=\frac{F_G}{m_2}=\frac{5,339\,N}{1,6\cdot 10^6\,kg}=\frac{5,339\,\frac{kg\cdot m}{s^2}}{1,6\cdot 10^6\,kg}=3,337\cdot10^{-6}\,\frac{m}{s^2}\)

In einem Hafen steht ein großes Containerschiff (\(m_1=400000\,t\)) neben einem Schlepper (\(m_1=20\,t\)). Der Abstand ihrer Schwerpunkte beträgt \(35\,m\). Wie groß ist die Schwerkraft die zwischen den beiden Schiffen wirkt? Nr. 2066
	\(F=0,003N\)
	\(F=0,052N\)
	\(F=0,436N\)
	\(F=3,827N\)
	\(F=12,917N\)
Lösungsweg Die Kraft zwischen zwei Objekten aufgrund der Gravitation wird durch dass Newtonsche Graviationsgesetz \(F_{G}=G\cdot \frac{m_1\cdot m_2}{r^2}\). \(m_1\) und \(m_2\) sind die Massen der zwei Objekte, \(r\) ist der Abstand der Schwerpunkte der zwei Objekte und \(G\) ist die Gravitationskonstante mit dem Wert \(G=6,67408 \cdot 10^{-11}\,\frac{m^3}{kg \cdot s^2}\). Die Massen der Schiffe in SI-Einheiten \(m_1=400\,000\,t=4\cdot 10^{8}\,kg\) und \(m_2=20\,t=2\cdot 10^4\,kg\) eingesetzt mit \(r=35\,m\) ergibt \(F_G=6,67408\cdot 10^{-11} \frac{4\cdot 10^{8}\cdot 2 \cdot 10^4}{35^2}=0,435858\,N\).

In einem Hafen steht ein großes Containerschiff (400.000t) neben einem Schlepper (20t). Der Abstand ihrer Schwerpunkte beträgt 35m. Wie lange braucht der Schlepper um sich nur durch die Anziehungskraft 10cm an das Containerschiff anzunähern? (Sämtliche Reibungen können vernachlässigt werden, das Containerschiff kann als starr angenommen werden. Die Bewegung kann als gleichförmig beschleunigte Bewegung angenommen werden.) Nr. 2067
	\(t=96s\)
	\(t=522s\)
	\(t=7239s\)
	\(t=28\ 482s\)
	\(t=365\ 182s\)
Lösungsweg Die Masse des Containerschiffes ist \(m_C=400\quad 000\,t=4\times 10^{8}\,kg\) und die Masse des Schleppers ist \(m_S=20\,t=2\times 10^4\,kg\). Laut Gravitationsgsetz ist die Kraft zwischen den Schiffen \(F=G \frac{m_C\cdot m_S}{r^2}\). Dies lässt sich mit einer Kraft auf den Schlepper \(F=m_S \cdot a\) gleichsetzen. Die Beschleunigung \(a\) hat dann die folgende Form \(a=G \cdot \frac{m_C}{r^2}\). Da das Containerschiff als konstant angesehen wird, betrachten wir die Ortsgleichung des Schleppers \(s(t)=s_0+v_0\cdot t+a\cdot\frac{t^2}{2}\). Sowohl der Anfangsort \(s_0\) als auch die Anfangsgeschwindigkeit \(v_0\) sind beide gleich Null,somit reduziert sich \(s(t)\) auf \(s(t)=a\cdot \frac{t^2}{2}\). Die Frage, wie lange es dauert, bis der Schlepper sich \(10\,cm\) an das Containerschiff angenähert hat, bedeutet zu welchem Zeitpunkt \(t\) ist \(s(t)=10\,cm=0,1\,m\). Wir formen \(s(t)\) nach \(t\) um: \(t=\sqrt{\frac{2\cdot s(t)}{a}}\). Für \(a\) setzen wir \(a=G \cdot \frac{m_C}{r^2}=6,674\times 10^{-11} \cdot \frac{4\times 10^8}{35^2}=0.0002179265\,\frac{m}{s^2}\) ein und mit \(s(t)=0,1\,m\) ergibt das für \(t=95,799\,s\)

Impulserhaltung: Ein Ball \((m_1=0,5kg)\) fliegt mit einer Geschwindigkeit von \(v=20\frac ms\) in die Arme des lotrecht hochgesprungenen Torwarts \((m_2=75kg)\), der ihn festhält. Mit welcher Geschwindigkeit \(\bar{v}\) fliegt der Torwart nach hinten? Nr. 2068
	\(\bar{v}=0,05\frac ms\)
	\(\bar{v}=0,09\frac ms\)
	\(\bar{v}=0,13\frac ms\)
	\(\bar{v}=0,19\frac ms\)
	\(\bar{v}=0,24\frac ms\)
Lösungsweg Das Fangen und Festhalten des Balles durch den Torwart entspricht einem inelastischen Stoß. Für diesen gilt allgemein, dass die Summe der Impulse vor \((p_i)\) und nach \((\bar{p}_i)\) dem Stoß muss gleich groß sein. \(\sum_i p_i=\sum_i \bar{p}_i\). Für \(i=1,2\) bedeutet dass \(m_1\cdot v_1 + m_2 \cdot v_2=(m_1 + m_2) \cdot \bar{v}\), wo \(\bar{v}\) die Geschwindigkeit beider Objekte nach dem Stoß ist: \(\bar{v}=\frac{m_1\cdot v_1 + m_2 \cdot v_2}{m_1+m_2}\). Da die Geschwindigkeit des Torwarts vor dem Stoß \(v_2=0\), ist \(\bar{v}=\frac{m_1\cdot v_1 }{m_1+m_2}=\frac{0,5 \,kg \cdot 20\,\frac{m}{s} }{0,5\,kg+75\,kg}=\frac{10 \,kg\cdot \frac{m}{s}}{75,5\,kg}=0,132\,\frac{m}{s}\)

Welche Kraft F wird benötigt, wenn ein Körper mit der Masse m=12kg in 4 Sekunden von 30 m/s auf 50 m/s beschleunigt? Nr. 3110
	\(F=60\,N\)
	\(F=30\,N\)
	\(F=70\,N\)
	\(F=40\,N\)
	\(F=80\,N\)
Lösungsweg \(F=m\cdot a\) Die Veränderung der Geschwindigkeit eines Objektes mit der Beschleunigung a von v1 auf v2 \(v2-v1=\Delta v=a\cdot t \rightarrow a=\frac{\Delta v}{t}\) und damit berechnet sich die Kraft F wie folgt \(F=12\cdot\frac{50-30}{4}=60\,N \)

Welche Masse \(m \) besitzt ein Körper, auf den die Kraft \(F=90\,N\) wirkt, während er in 2 Sekunden von \(100\, \frac{km}{h}\) auf \(130\, \frac{km}{h}\) beschleunigt wird? Nr. 3111
	\(m=23,5\,kg \)
	\(m=21,6kg\)
	\(m=21430\,g\)
	\(m=12,7\,g\)
Lösungsweg \(F=m\cdot a\) \(130 \,\frac{km}{h}=36,1\,\frac{m}{s} \qquad\text{und}\qquad 100\,\frac{km}{h}=27,8\,\frac{m}{s}\) \(90=m\cdot\(\frac{36,1-27,8}{2}\) \) \(\rightarrow m=21.69\,kg\)