
Sie können sich rechts oben einen kostenlosen Benutzer erstellen. Dann wird Ihr Lernfortschritt gespeichert, Sie können Tests zwischenspeichern und an Tutorien teilnehmen.
|
Ein wesentlicher Bestandteil der Fehlerfortpflanzung ist die partielle Ableitung. Leiten Sie folgende Formel nach x ab: \(f(x,y,z)=3x^2y^2z^4\) Nr. 2676
|
|
|---|---|
| Lösungsweg | |
|
Ein wesentlicher Bestandteil der Fehlerfortpflanzung ist die partielle Ableitung. Leiten Sie folgende Formel nach y ab: \(f(x,y,z)=3x^2y^2z^4\) Nr. 2677
|
|
|---|---|
| Lösungsweg | |
|
Ein wesentlicher Bestandteil der Fehlerfortpflanzung ist die partielle Ableitung. Leiten Sie folgende Formel nach z ab: \(f(x,y,z)=3x^2y^2z^4\) Nr. 2678
|
|
|---|---|
| Lösungsweg | |
|
Für die Rechengröße\(\bar{F}\) gilt: \( \bar{F}=\frac{\bar{n}^3}{7\bar{m}^2}\). Wie lautet die partielle Ableitung nach \(n\)? Nr. 2680
|
|
|---|---|
|
Gegeben seien die Größen \(m\) mit einem Mittelwert von \(\bar{m}=9,78\) und einer Standardabweichung \(\sigma= 0,16\) sowie n mit einem Mittelwert von \( \bar{n}=100,2\) und einer Standardabweichung von \(\sigma=0,079\). Für die Rechengröße \(\bar{F}\) gilt: \(\bar{F}=\frac{\bar{n}^3}{7\bar{m}^2}\). Wie lautet die partielle Ableitung nach \(m\)? Nr. 2681
|
|
|---|---|
|
Partielle Ableitungen sind ein wesentlicher Bestandteil der Fehlerfortpflanzungsrechnung. Leite die Gleichung \(F=\frac{3k^2}{p^3} \) partiell nach \(k\) ab! Nr. 2685
|
|
|---|---|
|
Leite die Gleichung \(F=\frac{3k^2}{p^3}\) partiell nach \(p\) ab! Nr. 2686
|
|
|---|---|
|
Gegeben sind folgende Größen: \(b\) mit \(\bar{b}=39,21\) und \(\sigma_{b}=7,21\) sowie \(c\) mit \(\bar{c}=12,45\) und \(\sigma_{c}=3,14\). Es gilt \(A=\frac{2b^3}{3c^2}\). Leite partiell nach \(b\) ab! Nr. 2691
|
|
|---|---|
|
Es gilt \(F=\frac{2b^3}{3c^2}\). Leite partiell nach \(c\) ab! Nr. 2693
|
|
|---|---|
|
Leite folgende Funktion partiell nach \(x\) ab: \(F=\frac{3xy}{z^2}\) Nr. 2695
|
|
|---|---|
|
Leite folgende Funktion partiell nach \(y\) ab: \(\frac{3xy}{z^2}\) Nr. 2696
|
|
|---|---|
|
Leite folgende Funktion partiell nach \(z\) ab \(F\left(x,y,z\right)=\frac{3xy}{z^2}\) Nr. 2697
|
|
|---|---|
| Lösungsweg | |
|
Gegeben ist die Funktion \(R\left.\left(x,y\right)\right.=\frac{y^3}{3x^2}\). Leite diese partiell nach \(x\) ab! Nr. 2700
|
|
|---|---|
| Lösungsweg | |
|
Es gilt \(R=\frac{y^3}{3x^2}\) - leite partiell nach \(y\) ab! Nr. 2701
|
|
|---|---|
|
Welche der folgenden Rechenregeln ist/sind für das partielle Ableiten relevant? Nr. 2702
|
|
|---|---|
|
Die Kettenregel... Nr. 2703
|
|
|---|---|
|
Die Produktregel... Nr. 2704
|
|
|---|---|
|
Bei der partiellen Ableitung wird eine Funktion mit mehreren Variablen nach einer Variablen abgeleitet. Wie werden die anderen Variablen dabei behandelt? Nr. 2705
|
|
|---|---|
|
Leite \(\frac{3x^2}{4yz^2}\) nach \(x\) ab. Nr. 2706
|
|
|---|---|
| Lösungsweg | |
|
Leite \(\frac{3x^2}{4yz^2}\) nach \(y\) ab. Nr. 2707
|
|
|---|---|
| Lösungsweg | |
|
Leite \(\frac{3x^2}{2yz^2}\) nach \(z\) ab. Nr. 2708
|
|
|---|---|
| Lösungsweg | |
|
Leite folgende Gleichung nach \(x\) ab. \(F(x,\ y)=cos(x)+sin(yx)\) Nr. 4385
|
|
|---|---|
| Lösungsweg | |
|
Leite nach \(x\) ab.
\(F(x,\ y,\ \omega)=\e^{-xy}\,sin(\omega x)\) Nr. 4386
|
|
|---|---|
| Lösungsweg | |
|
Bilden Sie die Partiellen Ableitungen erster und zweiter Ordnung der Funktion \(f(x,\, y)=xy^2+4 x^5y+16x+27\). Nr. 4403
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei das Skalarfeld \(u(x,y)=2x+y^2\). Bilde den Gradienten von \(u(x,y)\). Nr. 4528
|
|
|---|---|
| Lösungsweg | |
|
Du willst mithilfe eines Fadenpendels die Erdbeschleunigung \(g\) experimentell ermitteln. Dafür misst du die Periodendauer \(T\) einer Schwingung mehrere Male und bildest aus deinen Ergebnissen einen Mittelwert und die Standardabweichung. Du kommst auf \(T=(1.66 \pm 0.02)s\). Außerdem misst du die Länge \(l\) des Fadens mit einem Maßband. Die Unsicherheit der Längenmessung ist die kleinste Einheit auf dem Maßband, also 1mm. Du misst \(l=(60.0 \pm 0.1)cm\). Aus der Formel \(g=4 \cdot \pi^2 \frac{l}{T^2}\) willst du nun die Erdbeschleunigung ausrechnen. Wie lautet dein Ergebnis und vor allem: wie lautet die Unsicherheit? 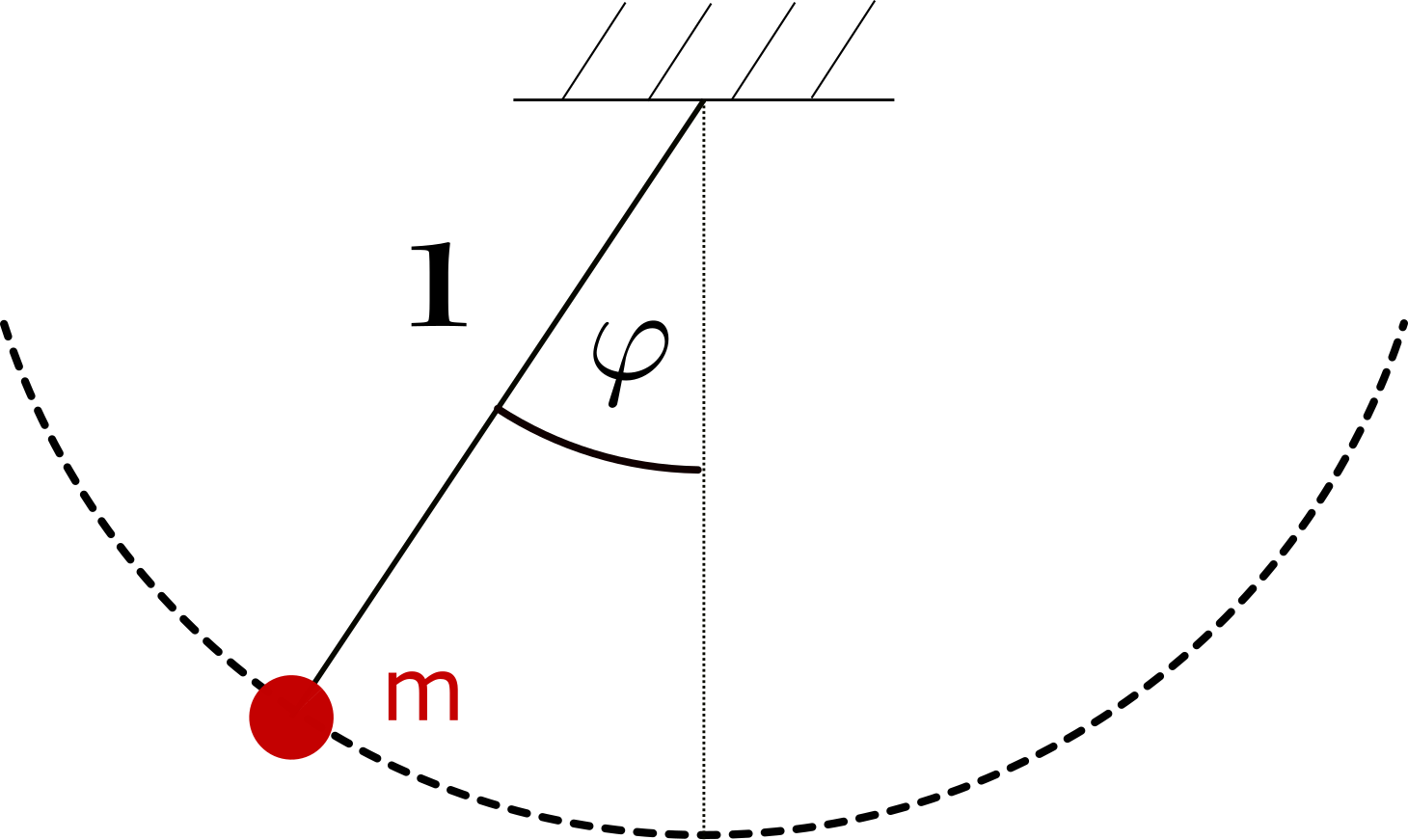 Nr. 4569
|
|
|---|---|
| Lösungsweg | |
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!

Sie können sich rechts oben einen kostenlosen Benutzer erstellen. Dann wird Ihr Lernfortschritt gespeichert, Sie können Tests zwischenspeichern und an Tutorien teilnehmen.