Fragenliste von Das magnetische Feld
|
An der Nordhalbkugel hat das Erdmagnetfeld an einer bestimmten Stelle eine Stärke von \(0,6 \ \ G\) (Einheit Gauß) und ist nach unten, sowie nach Norden gerichtet, wobei es einen Winkel von etwa \(70^\circ\) mit der Horizontalen einschließt. Ein Proton \((q=+e)\) bewegt sich mit einer Geschwindigkeit von \(\vec{v} = \begin{pmatrix}0\\\ 10^7\\0\end{pmatrix} m/s \) horizontal nach Norden. Berechne die auf das Proton wirkende magnetische Kraft a) mittels \(|F| = q|v||B|\sin \theta\) und b) vektoriell als \(\vec{F} = q({\vec{v} \times \vec{B})\), indem v und B in Komponentenschreibweise mit den Einheitsvektoren \(\hat{\vec{x}}\), \(\hat{\vec{y}} \)und \(\hat{\vec{Z}} \)formuliert werden Nr. 2841
|
|
|---|---|
| Lösungsweg | |
|
Durch einen \(L = 5 mm\) langen Drahtabschnitt fließt in positiver x-Richtung ein Strom von \(5 A\). Der Leiter ist von einem Magnetfeld mit einer Feldstärke von \(0,030 T\) (Tesla) umgeben, dessen Vektor in der x-y-Ebene liegt und einen Winkel von \(30^\circ\) mit der x-y-Ebene einschließt. Berechne die auf den Leiterabschnitt wirkende magnetische Kraft.
Nr. 2842
|
|
|---|---|
| Lösungsweg | |
|
In einem geraden stromdurchflossenen Leiterabschnitt befindet sich das Stromelement \(IL\) mit \(I = 3,8 A \) und \(L = (2 \hat{\vec{x}} + 5 \hat{\vec{y}}) \) \(cm\) . Es ist von einem homogenen Magnetfeld \(B = 2,4 \hat{\vec{x}} T \)umgeben \((\theta = 30^\circ)\) . Berechne die auf den Leiterabschnitt wirkende Kraft. \(\vec{x}} \)...Einheitsvektor in x Richtung \(\vec{y}} \)...Einheitsvektor in y-Richtung Nr. 2843
|
|
|---|---|
| Lösungsweg | |
|
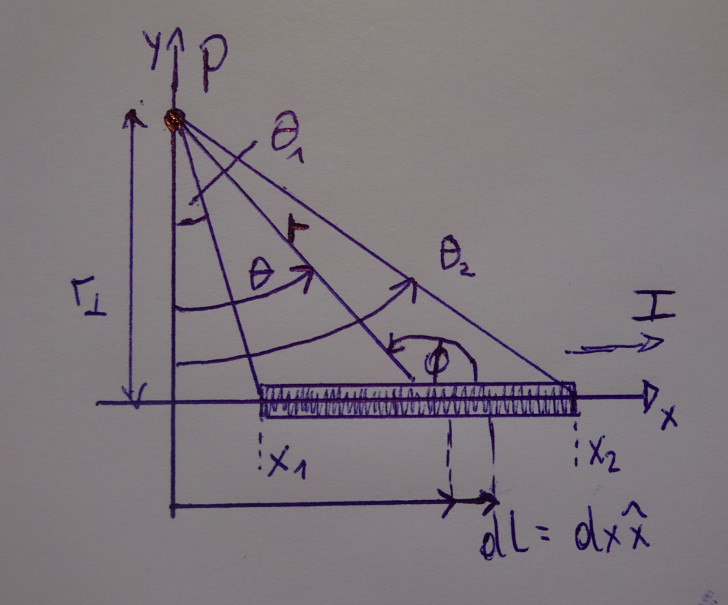
Ein zu einem Halbkreis mit Radius r gebogener Leiter liegt in der x-y-Ebene. Zwischen den Punkten a und b fließt ein Strom \(I\). Den Leiter umgibt ein sekrecht zur Ebene des Halbkreis gerichtetes Magnetfeld \(\vec{B} = B\hat{\vec{z}}\). Welche magnetische Kraft wirkt auf den halbkreisförmigen Leiterabschnitt? Zur Berechnung dieses Beispiels wandle die x-y-Koordinaten in Abhängigkeit des Winkel \(\theta\) an. \((\theta = 0 \ \ bis\ \ \theta = \pi)\) Nr. 2844
|
|
|---|---|
| Lösungsweg | |
|
Ein Proton mit der Masse \(m = 2,48 \dot 10^{-27}kg\) und der Ladung \(q = e = 1,6 \cdot 10^{-19} C\) bewegt sich auf einer Kreisbahn mit einem Radius \(r = 42 cm\) senkrecht zu einem Magnetfeld mit \(|B| = 6000 G\). Berechne die Geschwindigkeit \(v \) des Protons. Nr. 2845
|
|
|---|---|
| Lösungsweg | |
|
Ein Proton mit der Masse \(m = 2,48 \dot 10^{-27}kg\) , Geschwindigkeit \(v =1,62 \cdot 10^7 m/s\) und der Ladung \(q = e = 1,6 \cdot 10^{-19} C\) bewegt sich auf einer Kreisbahn mit einem Radius \(r = 42 cm\) senkrecht zu einem Magnetfeld mit \(|B| = 6000 G\). Berechne die Persiode \(T \) der Bewegung. Nr. 2846
|
|
|---|---|
| Lösungsweg | |
|
Ein Zyklotron arbeitet mit einem Magnetfeld von \(0,340 T\), der maximale Radius beträgt \(0,7 m\). Das Proton trägt Ladung \(q = e = 1,6 \cdot 10^{-19} C\) und Masse \(m = 1,67 \cdot 10^{-27}\) . Gib die Zyklotronfrequenz \(f\) an.
Nr. 2847
|
|
|---|---|
| Lösungsweg | |
|
Ein Zyklotron arbeitet mit einem Magnetfeld von \(0,340 T\), der maximale Radius beträgt \(0,7 m\). Das Proton trägt Ladung \(q = e = 1,6 \cdot 10^{-19} C\) und Masse \(m = 1,67 \cdot 10^{-27}\) und hat die Zyklotronfrequenz von \(f= 5,2 MHz\). Mit welcher kinetischen Energie \(E_{kin}\) treten die Protonen aus dem Zyklotron aus? Nr. 2848
|
|
|---|---|
| Lösungsweg | |
|
Ein punktförmiges Teilchen mit einer Ladung \(q = - 4,56 nC\) bewegt sich mit einer Geschwindigkeit von \(3,54 \cdot 10^6 \hat{\vec{x}} m/s\). Berechne die Kraft, die ein Magnetfeld \(B = 0,45 \hat{\vec{y}} T\) auf das Teilchen ausübt.
Nr. 2849
|
|
|---|---|
| Lösungsweg | |
|
Ein Elektron \((q= -e)\) mit einer kinetischen Energie von \(5 keV\) bewegt sich auf einer Kreisbahn, die sich in einem senkrecht zur Bahn gerichteten Magnetfeld mit einer Feldstärke von \(0,487 T\) befindet Berechne den Radius \(r\) der Bahn.
Nr. 2850
|
|
|---|---|
| Lösungsweg | |
|
Ein Elektron \((q= -e)\) mit einer Kinetischen Energie von \(5 keV\) bewegt sich auf einer Kreisbahn mit Radius \(r= 2 mm\), die sich in einem senkrecht zur Bahn gerichteten Magnetfeld mit einer Feldstärke von \(0,487 T\) befindet. Berechne die Frequenz \(f\) und die Periode \(T\) der Kreisbewegung. Nr. 2851
|
|
|---|---|
| Lösungsweg | |
|
Ein Massepunkt mit der Ladung \(q = 3,5 \mu C\) bewegt sich mit der Geschwindigkeit \(\vec{v} = (4 \cdot 10^3 \hat{\vec{x}}) m/s\) parallel zur x-Achse in der Ebene mit \(z = 0\) entlang der Linie mit \(y = 3 m\). Wie groß ist das von dieser Ladung im Koordinatenursprung erzeugte Magnetfeld wenn sich die Ladung im Punkt \( P = (-4,3)\) befindet?
Nr. 2852
|
|
|---|---|
| Lösungsweg | |
|
Ein Proton mit der Ladung \(q = 5,6 \mu C \) bewegt sich mit der Geschwindigkeit \(\vec{v} = (2,5 \cdot 10^3 \hat{\vec{x}}) m/s\) parallel zur x-Achse in der Ebene mit \(z = 0\) entlang der Linie mit \(y = 5 m\). Wie groß ist das von dieser Ladung im Koordinatenursprung erzeugte Magnetfeld wenn sich die Ladung im Punkt \(P = (-5,5)\) befindet?
Nr. 2853
|
|
|---|---|
| Lösungsweg | |
|
Eine Leiterschleife mit kreisförmigem Querschnitt hat \(5 \ \ Windungen \ \ (n = 5)\), mit dem Radius von \(r=5 cm\). Durch diese fließt ein Strom von \(I=6 A\). Berechne die im Draht bewegte Ladung (in Coulomb) unter der Annahme, dass die Driftgeschwindigkeit der freien Elektronen gleich \(v_d=1,4 \cdot 10^{-4} m/s \) ist.
Nr. 2854
|
|
|---|---|
| Lösungsweg | |
|
Berechne das Magnetfeld im Mittelpunkt einer quadratischen Leiterschleife mit der Seitenlänge \(L = 40 cm\), durch die ein Strom von \(2,5 A \) fließt.
 Nr. 2855
|
|
|---|---|
| Lösungsweg | |
|
Zwei lange, gerade Leiter liegen parallel zur z-Achse entlang der Linie mit \(x = -3 cm\) und \(y = 0\) bzw. mit \(x = 3\) und \(y = 0\). Durch beide Leiter fließt in positiver z-Richtung ein Strom von \(1,7 A\). Berechne das Magnetfeld im Punkt P auf der y- Achse bei \(y = 6 cm\).
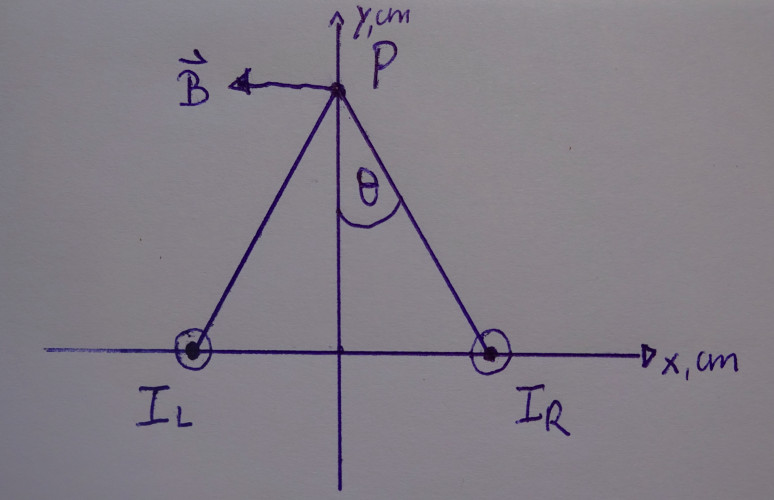 Nr. 2856
|
|
|---|---|
| Lösungsweg | |
|
Ein einfach geladenes (\(q = 1e\)) Molekül mit Masse \(m = 5,35\cdot 10^{-25}kg\) wird in einer Potentialdifferenz von \(U = 50kV\) beschleunigt. Danach tritt es in ein homogenes Magnetfeld ein, welches normal auf die Flugrichtung des Moleküls steht. Wie stark muss das Magnetfeld sein, damit das Molekül auf eine Kreisbahn mit Radius \(r = 1m\) abgelenkt wird? Nr. 4150
|
|
|---|---|
| Lösungsweg | |
|
Zwei stromdurchflossene gerade Leiter verlaufen parallel mit \(10\ cm\) Abstand zueinander. Ihre Ströme fließen in die selbe Richtung mit je \(40\ A\). Welche Arbeit muss aufgewendet werden, um diese Leiter entlang einer Länge von \(35\ m\) auf \(30\ cm\) auseinander zu bringen? Nr. 4381
|
|
|---|---|
| Lösungsweg | |
|
Was ist die Einheit der magnetischen Feldstärke? Nr. 4383
|
|
|---|---|
| Lösungsweg | |
|
Wie lautet die Maxwellgleichung für Magnetfelder (auch Gauß'sches Gesetz für Magnetfelder genannt)? Nr. 4399
|
|
|---|---|
| Lösungsweg | |
NEWS
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!




 mit der Geschwindigkeit
mit der Geschwindigkeit  durch ein magnetisches Feld
durch ein magnetisches Feld 
