Fragenliste von Die magnetische Induktion - Induktionsspannung
|
Zwei Leiterschleifen sind parallel zueinander angeordnet. In der Schleife A fließt, von links gegen die Ebenen der Schleifen gesehen, ein Strom entgegengesetzt dem Uhrzeigersinn. In welcher Richtung fließt der Strom in Schleife B, wenn die Stromstärke in A zunimmt? Entscheide, ob die Schleifen einander abstoßen oder anziehen.  Nr. 2857
|
|
|---|---|
| Lösungsweg | |
|
Ein Stabmagnet ist so am Ende einer Spiralfeder befestigt, dass er eine einfache harmonische Bewegung entlang der Achse einer Leiterschleife ausführt (siehe Bild). Der Magnet befindet sich im Gleichgewicht, wenn sein mittelpunkt in der Ebene der Schleife liegt. Wie verläuft der Fluss \( \Phi_{mag}\) durch die Schleife in Abhängigkeit von der Zeit bzw. wie verläuft der induzierte Strom durch die Schleife in Abhängigkeit von der Zeit? 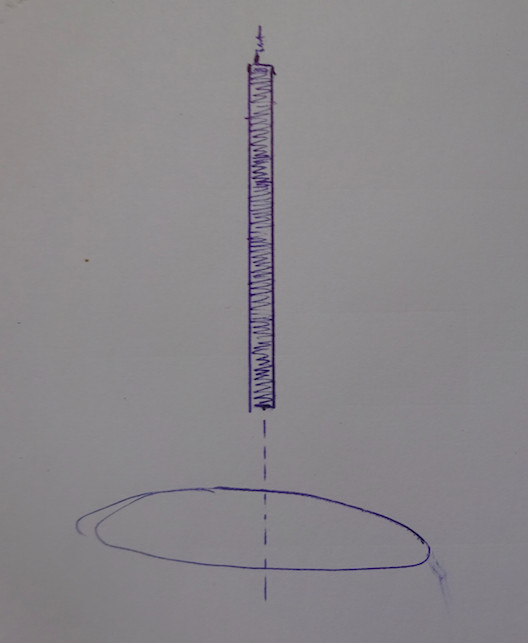 Nr. 2858
|
|
|---|---|
|
Eine kreisrunde Spule mit \(300 \ \ Windungen\) und einem Radius vom \(4 cm\) schließt einen Winkel von \(30^\circ\) mit der Richtung eines homogenen äußeren Magnetfelds ein. Die Stärke des Magnetfelds nimmt pro Sekunde um \(85 T\) zu, ohne dass sich die Richtung des Felds ändert. Wie groß ist die in der Spule induzierte Spannung?
Nr. 2860
|
|
|---|---|
| Lösungsweg | |
|
Eine kreisrunde Spule mit \(300 \ \ Windungen\) und einem Radius vom \(8cm\) schließt einen Winkel von \(45^\circ\) mit der Richtung eines homogenen äußeren Magnetfelds ein. Die Stärke des Magnetfelds nimmt pro Sekunde um \(56 T\) zu, ohne dass sich die Richtung des Felds ändert. Wie groß ist die in der Spule induzierte Spannung?
Nr. 2861
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei eine rechteckige Spule mit \(n \ \ Windungen\) sowie den Seitenlängen \(a \) und \(b\); es sei \(n = 80\), \(a = 20 cm\) und \(b = 30 cm\). Die Spule befindet sich zur Hälfte in einem Magnetfeld mit der Sträke von\( 0,8 T\), das in die Papierebene hineinzeigt. Der Widerstand der Spule ist \(30 \Omega\). Berechne den Betrag und die Richtung des induzierten Stroms, wenn sich die Spule mit einer Geschwindigkeit von \(2 m/s\) nach rechts bewegt?
Nr. 2862
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei eine rechteckige Spule mit \(n \ \ Windungen\) sowie den Seitenlängen \(a \) und \(b\); es sei \(n = 80\), \(a = 20 cm\) und \(b = 30 cm\). Die Spule befindet sich zur Hälfte in einem Magnetfeld mit der Stärke von\( 0,8 T\), das in die Papierebene hineinzeigt. Der Widerstand der Spule ist \(30 \Omega\). Berechne den Betrag und die Richtung des induzierten Stroms, wenn sich die Spule mit einer Geschwindigkeit von \(2 m/s\) in der Papierebene nach oben bewegt?
Nr. 2863
|
|
|---|---|
| Lösungsweg | |
|
Berechne die Selbstinduktivität einer \(10 cm\) langen Zylinderspule mit \(100\ \ Windungen\) und einer Querschnittsfläche von \(5 cm^2\). Nr. 2864
|
|
|---|---|
| Lösungsweg | |
|
Welche der Maxwell-Gleichungen beschreibt das Induktionsgesetz? Nr. 4110
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei ein idealer Transformator, mit primärseitig \(N_1 = 80\) Windungen und sekundärseitig \(N_2 = 200\) Windungen. Primärseitig ist eine Gleichspannung von \(U_1 = 10V\) angelegt. Welche Spannung \(U_2\) wird sekundärseitig induziert? Nr. 4111
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei ein idealer Transformator, mit primärseitig \(N_1 = 80\) Windungen und sekundärseitig \(N_2 = 200\) Windungen. Primärseitig ist eine Wechselspannung von \(U_1 = 10V\) angelegt. Welche Spannung \(U_2\) wird sekundärseitig induziert? Nr. 4112
|
|
|---|---|
| Lösungsweg | |
|
An einen idealen Transformator ist eine Eingangsspannung von \(U_1 = 230V\) angelegt. Er induziert eine Ausgangsspannung von \(U_2 = 50V\). In welchem Verhältnis steht die sekundärseitige Windungszahl \(N_2\) zur primärseitigen Windungszahl \(N_1\)? Nr. 4113
|
|
|---|---|
| Lösungsweg | |
|
Wie lautet die Lenz'sche Regel? Nr. 4382
|
|
|---|---|
NEWS
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!





