Fragenliste von Kinematik mit Differentialrechnung
|
Gegeben sei die Bewegungsgleichung: \(x(t)=9t^2+24\) Bestimmen Sie die Beschleunigung zum Zeitpunkt t. Nr. 2035
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung: \(x(t)=9t^2+24\) Bestimmen Sie die Geschwindigkeit zum Zeitpunkt t. Nr. 2036
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung eines Körpers: \(x(t)=9t^2+24\) Wie schnell ist der Körper bei \(x=60\,m\)? Nr. 2038
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung eines Körpers: \(x(t)=9t^3+24t\) Wie groß ist die Geschwindigkeit zum Zeitpunkt t? Nr. 2040
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung eines Körpers: \(x(t)=9t^3+24t\) Wann hat der Körper eine Geschwindigkeit von \(456\frac ms\) erreicht? Nr. 2041
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung eines Körpers: \(x(t)=9t^3+24t\) Welche Beschleunigung erfährt der Körper, wenn er eine Geschwindigkeit \(v=456\frac ms\) erreicht? Nr. 2042
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Geschwindigkeit hat der Körper zum Zeitpunkt t? Nr. 2366
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Beschleunigung hat der Körper zum Zeitpunkt t? Nr. 2367
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Geschwindigkeit hat der Körper bei \(x=28\,m\)? Nr. 2368
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Geschwindigkeit hat der Körper bei \(x=12\,m\)? Nr. 2369
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Geschwindigkeit hat der Körper zum Zeitpunkt \(t=3\,s\)? Nr. 2370
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Beschleunigung \(a\) hat der Körper bei \(x=29\,m\)? Nr. 2371
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung \(x(t)=4t^2+12\). Welche Beschleunigung \(a\) hat der Körper bei \(x=17\,m\)? Nr. 2372
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung: \(x(t)=-2t^4+3t\) Wie schnell ist der Körper zum Zeitpunkt t? Nr. 2373
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung: \(x(t)=-2t^4+3t\) Welche Beschleunigung hat der Körper zum Zeitpunkt t? Nr. 2374
|
|
|---|---|
|
Gegeben sei die Bewegungsgleichung: \(x(t)=-2t^4+8t\) Welche Geschwindigkeit hat der Körper bei x=6? Nr. 2375
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung: \(x(t)=-2t^4+8t\) Welche Beschleunigung hat der Körper bei x=6? Nr. 2376
|
|
|---|---|
| Lösungsweg | |
|
Gegeben ist die Bewegungsgleichung: \(x(t)=-3t^3+36t+12\) Wo ist der Körper in positiver Weg- und Zeitrichtung, wenn er am weitesten vom Ursprung entfernt ist? Nr. 2377
|
|
|---|---|
| Lösungsweg | |
|
Gegeben ist die Bewegungsgleichung: \(x(t)=-3t^3+36t+12\) Wann ist der Körper in positiver Weg- und Zeitrichtung am weitesten vom Ursprung entfernt? Nr. 2378
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Bewegungsgleichung: \(x(t)=4t^3+5t^2+8\) Welche Beschleunigung erfährt der Körper zum Zeitpunkt t? Nr. 3121
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Geschwindigkeitsgleichung: \(v(t)=3t^2+4t+5\) Wie hoch ist die Beschleunigung zum Zeitpunkt t? Nr. 3122
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Bewegungsgleichung: \(x(t)=4t^2+5t+3\) Welche Geschwindigkeit hat das Objekt zum Zeitpunkt t? Nr. 3176
|
|
|---|---|
| Lösungsweg | |
|
Gegeben ist folgende Geschwindigkeitgleichung: \(v(t)=7t+5\) Welche Beschleunigung erfährt der Körper zum Zeitpunkt t? Nr. 3177
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Bewegungsgleichung: \(x(t)=9t^3+4t^2+4t+8\) Welche Beschleunigung \(a(t)\) erfährt der Körper zum Zeitpunkt \(t\)? Nr. 3178
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Geschwindigkeitsgleichung: \(v(t)=16t+5\) Welche Beschleunigung erfährt der Körper zum Zeitpunkt t? Nr. 3179
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Beschleunigungsgleichung: \(a(t)=3t^2+8t-4\) Welche Beschleunigung erfährt ein Objekt zum Zeitpunkt \(t=5\)? Nr. 3180
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Geschwindigkeitsgleichung: \(v(t)=4t^2-2t+10\) Welche Beschleunigung erfährt ein Objekt zum Zeitpunkt \(t=9\)? Nr. 3181
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei ein Objekt, dass durch die Bewegungsfunktion \(s(t)=8t^3+6t^2-2t+3\) beschrieben wird. Welche Geschwindigkeit hat das Objekt zum Zeitpunkt \(t=8\)? Nr. 3398
|
|
|---|---|
| Lösungsweg | |
|
Die Bewegungsfunktion eines Objekts lautet \(s(t)=3t^3+9t^2-12t+4\). Welche Beschleunigung erfährt das Objekt zum Zeitpunkt \(t=3\)? Nr. 3399
|
|
|---|---|
| Lösungsweg | |
|
Die Bewegung eines Objekts wird beschrieben durch \(s(t)=3t^3+9t^2-12t+4\). Welche Geschwindigkeit hat das Objekt zum Zeitpunkt \(t=4\)? Nr. 3400
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Geschwindigkeitsfunktion \(v(t)=5t^3-2t^2+8t\). Wie hoch ist die Beschleunigung zum Zeitpunkt \(t=6\)? Nr. 3401
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Bewegungsgleichung \(s(t)=14t^3-20t^2+4t-9\) Welche Geschwindigkeit hat das Objekt bei \(t=7\)? Nr. 3402
|
|
|---|---|
| Lösungsweg | |
|
Die Bewegung eines Objekts wird beschrieben durch \(s(t)=2t^3-10t^2+10t-6\). Welche Beschleunigung erfährt das Objekt zum Zeitpunkt \(t=2\)? Nr. 3403
|
|
|---|---|
| Lösungsweg | |
|
Die Bewegung eines Objekts wird beschrieben durch die Bewegungsfunktion \(s(t)=4t^4-9t^3-8t^2+5t+3\) . Welche Geschwindigkeit hat das Objekt zum Zeitpunkt \(t=5\) Nr. 3404
|
|
|---|---|
| Lösungsweg | |
|
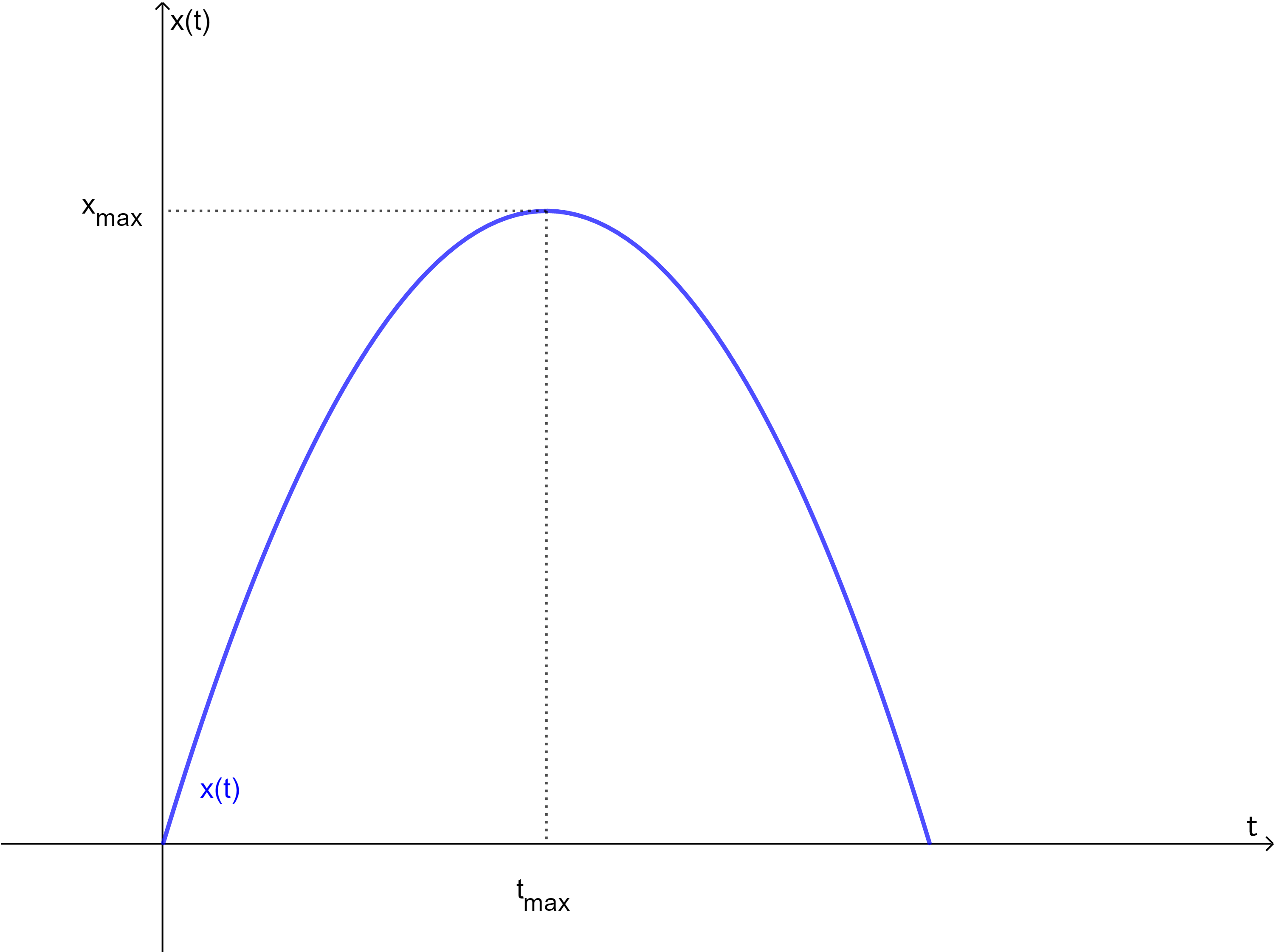
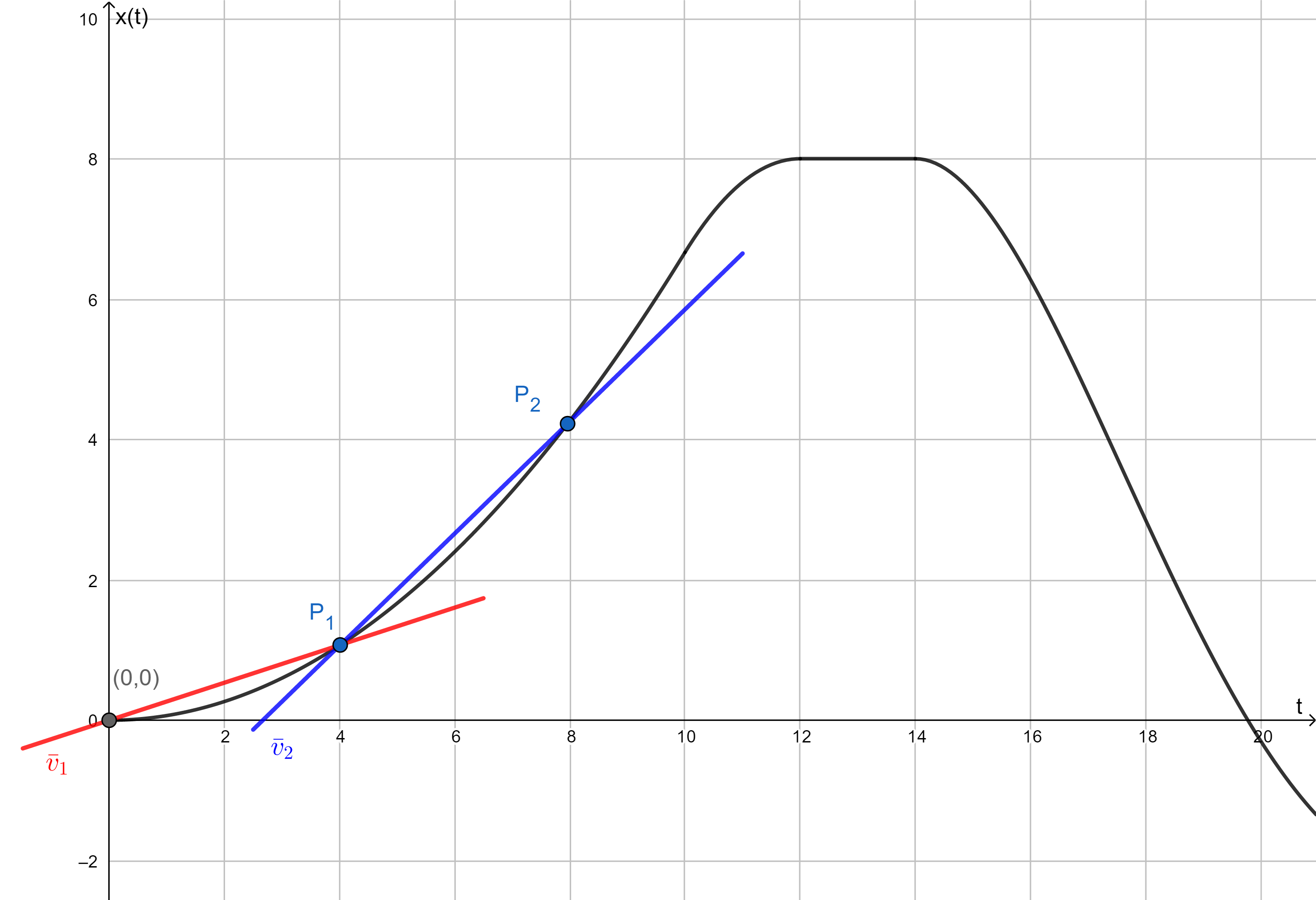
Gegeben sei die Bewegungsfunktion und ihre Tangente. Was wird hier grafisch dargestellt? Nr. 3518
|
|
|---|---|
| Lösungsweg | |
|
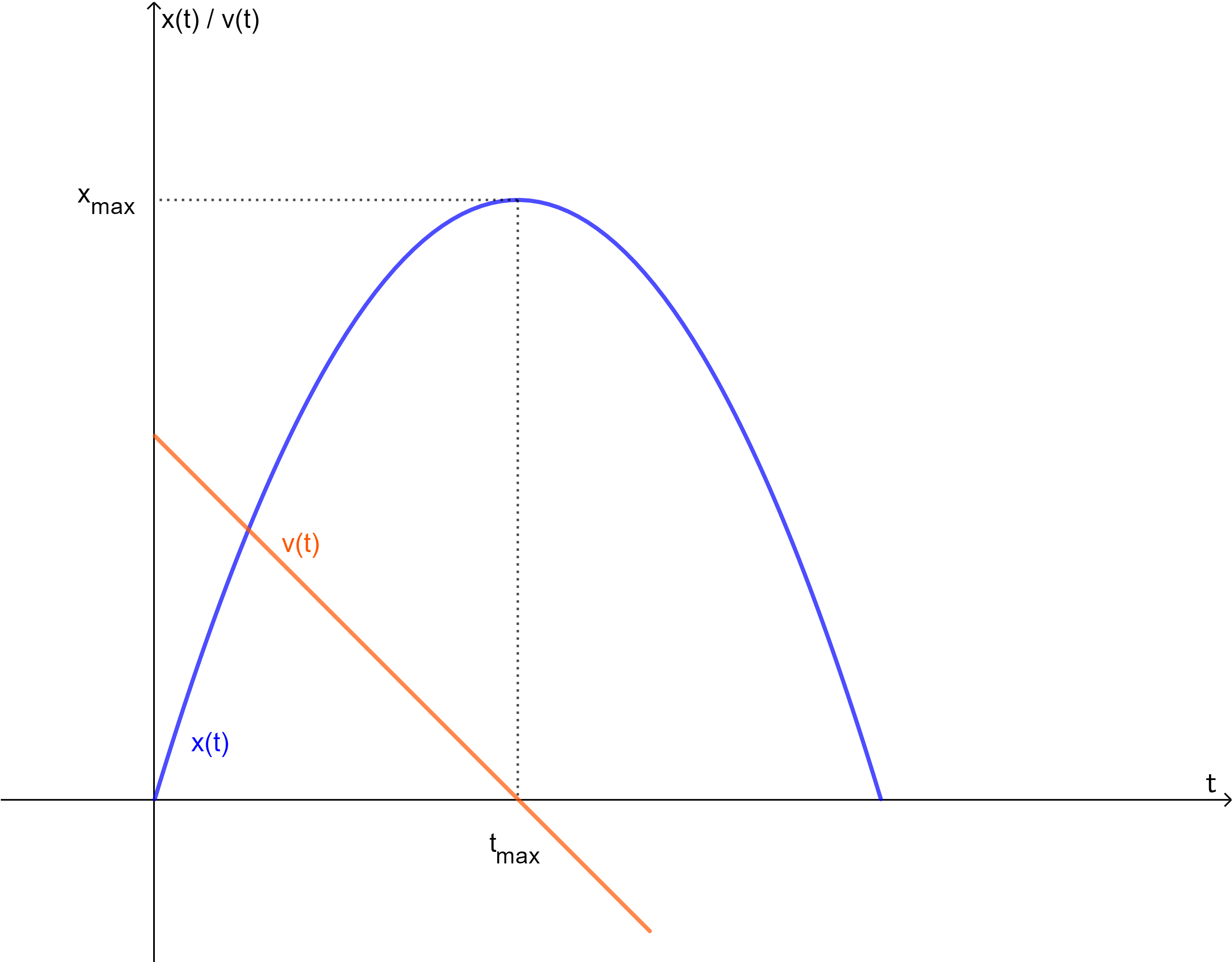
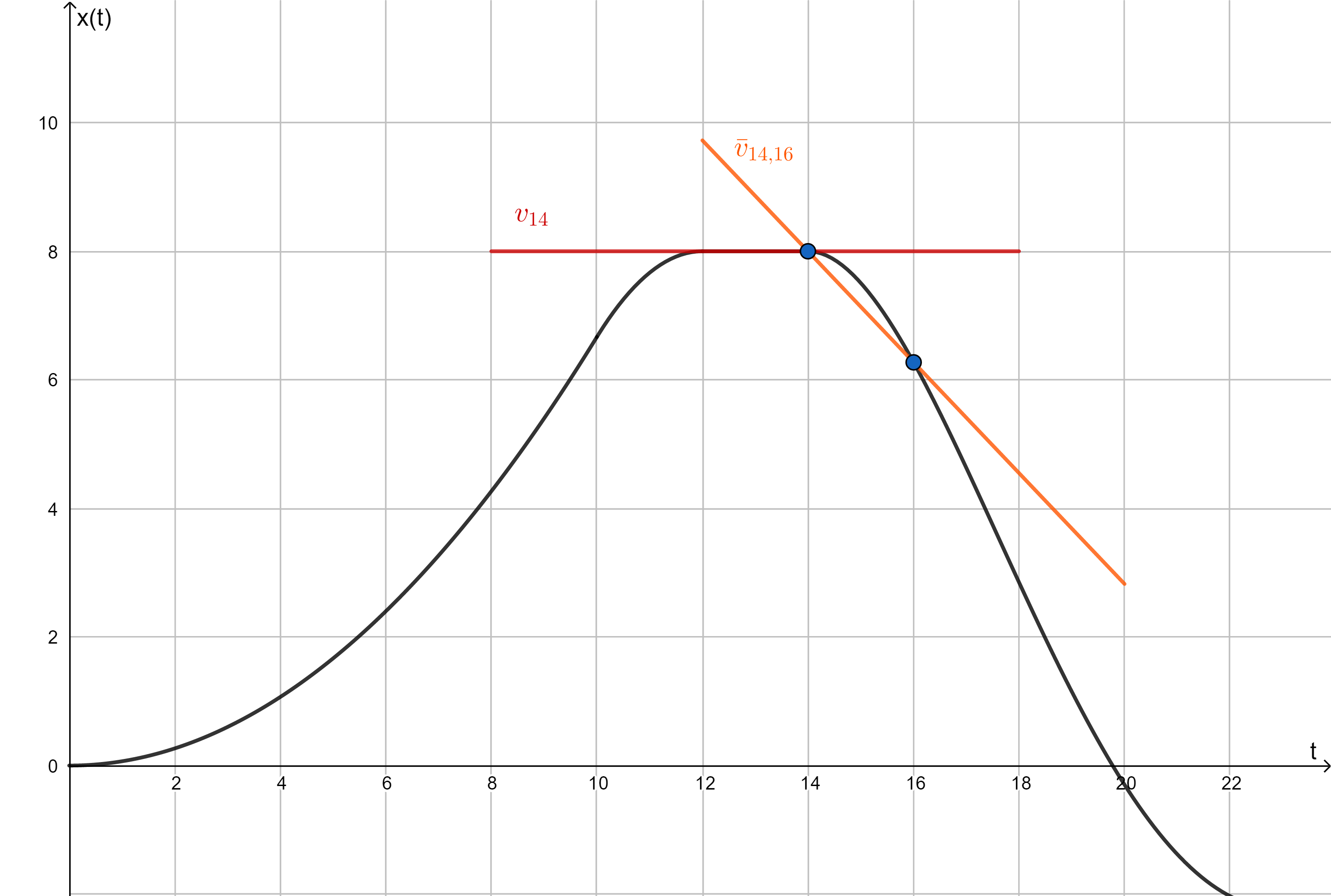
Abgebildet ist eine Geschwindigkeitsfunktion mit dazugehöriger Sekante. Was ist hier grafisch dargestellt? Nr. 3520
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Geschwindigkeitsfunktion. Was drückt die markierte Fläche aus? Nr. 3521
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei folgende Beschleunigungsfunktion. Was drückt die markierte Fläche aus? Nr. 3522
|
|
|---|---|
| Lösungsweg | |
|
Die Beschleunigung \(a=a(x)=b\cdot x^{3}\), bezüglicher derer \(x=x(t)\) gelten soll und \(b\) als konstant vorausgesetzt wird, sei als Funktion des Ortes bekannt. Wie lautet die Form der Geschwindigkeitsfunktion \(v(x)\) für die Anfangsbedingungen \(v_0\ :=\ v(x_{0})\)? Nr. 4167
|
|
|---|---|
| Lösungsweg | |
|
Die Bahnkurve \(x=x(t)\) eines Punktteilchens erfülle die Bewegungsgleichung \(\ddot{x}+2\dot{x}+x=2+t\). Wie lautet die Lösung dieser inhomogenen Differentialgleichung Nr. 4178
|
|
|---|---|
| Lösungsweg | |
|
Eine Bahnkurve \(z=z(t)\) erfülle die Bewegungsgleichung \(\ddot{z}+z=0\). Wie lautet die Lösung dieser homogenen Differentialgleichung für die Anfangsbedingungen \(z(0)=0\) und \(z(\frac{\pi}{2})=1\)? Nr. 4179
|
|
|---|---|
| Lösungsweg | |
|
Wie lautet die Lösung der Differentialgleichung \(\ddot{x}+\omega^{2}x=0\) für den linearen harmonischen Oszillator, wobei \(\omega=2\pi \nu\) die Kreisfrequenz bezeichnet.
Nr. 4182
|
|
|---|---|
| Lösungsweg | |
|
Ein linearer harmonischer Oszillator (\(\omega^2 = \frac{k}{m} , \) \(k\): Federkonstante, \(m\): Masse) erfahre Dämpfung durch Wirkung Stokes'scher Reibung \(F_{R} = - \alpha \dot{x}\)). Wie lautet die zugehörige Bewegungsgleichung? Wie lautet ihre Lösung? Nr. 4185
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei eine (stetige) Ortsfunktion \(x(t)\) (mit \(t \ \mathrm{in} \ s\) und \(x\ \mathrm{in} \ m\)), die folgende Eigeschaften besitzt:
Welche Aussagen treffen auf jeden Fall zu? Nr. 4423
|
|
|---|---|
| Lösungsweg | |
|
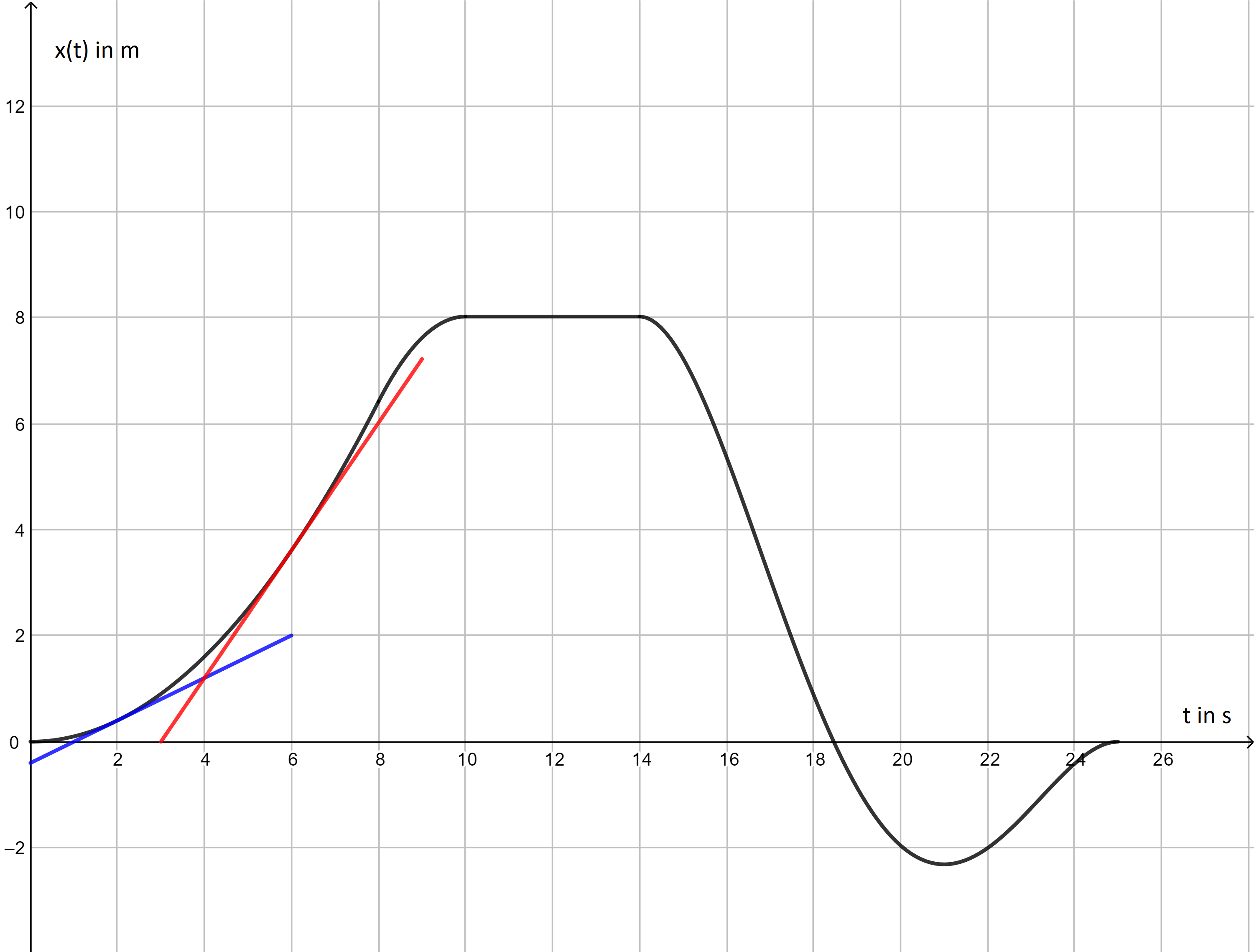
Gegeben ist ein Weg-Zeit-Diagramm, das eine geradlinige Bewegung eines Körpers in den Zeiten \(t \in \, [0,\ 25]\) (in Sekunden) beschreibt. Welche der Aussagen treffen/trifft zu? 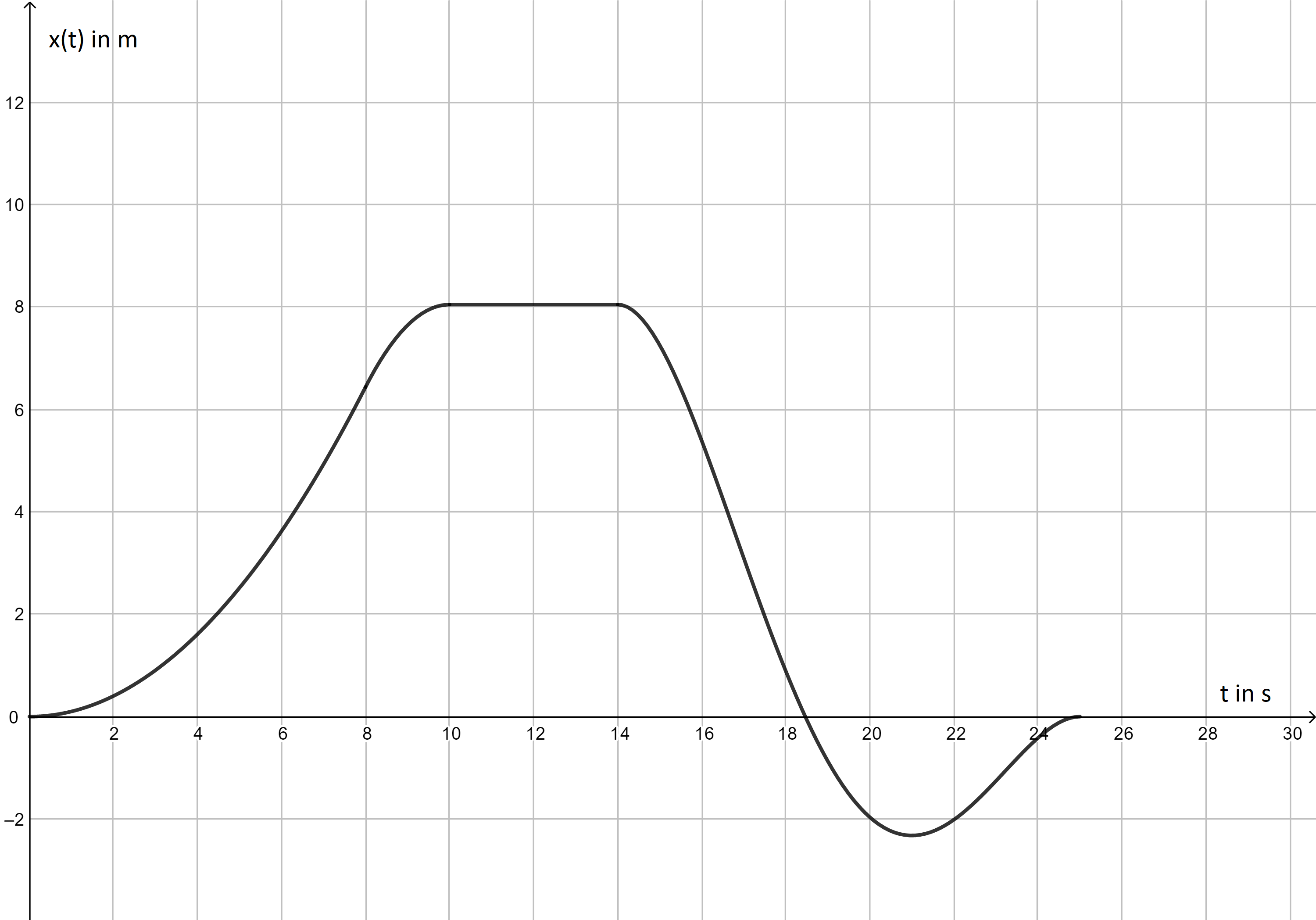 Nr. 4429
|
|
|---|---|
| Lösungsweg | |
|
Ein Körper wird mit einer Geschwindigkeit \(v_0\) senkrecht nach oben geworfen. Die Erdbeschleunigung wird mit \(g\) bezeichnet. Welche maximale Höhe \(x_{max}\) erreicht der Körper beim Wurf? Nr. 4437
|
|
|---|---|
| Lösungsweg | |
|
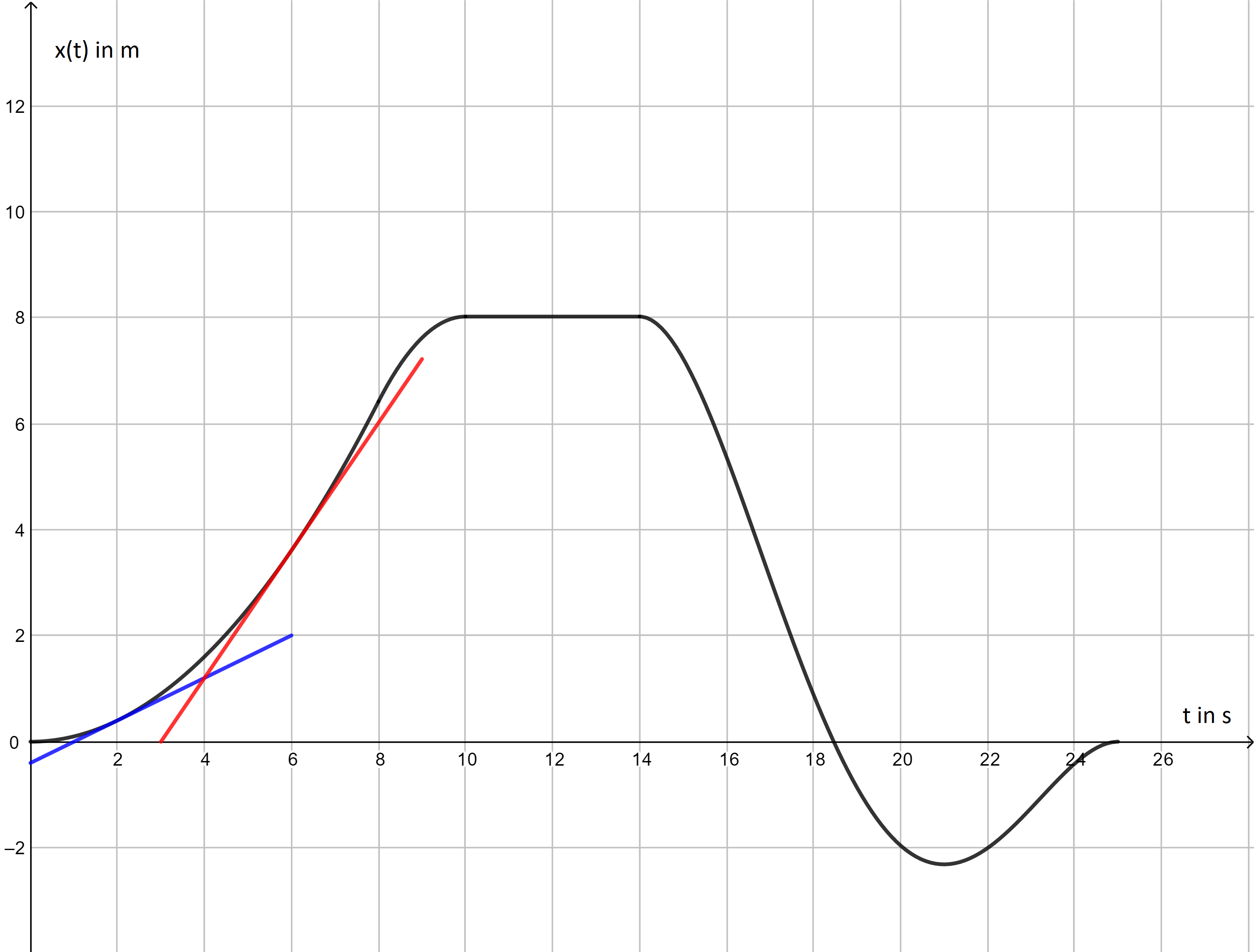
Gegeben sei folgendes Weg-Zeit-Diagramm, das die geradlinige Bewegung eines Körpers beschreibt. Welche der Aussagen sind korrekt? 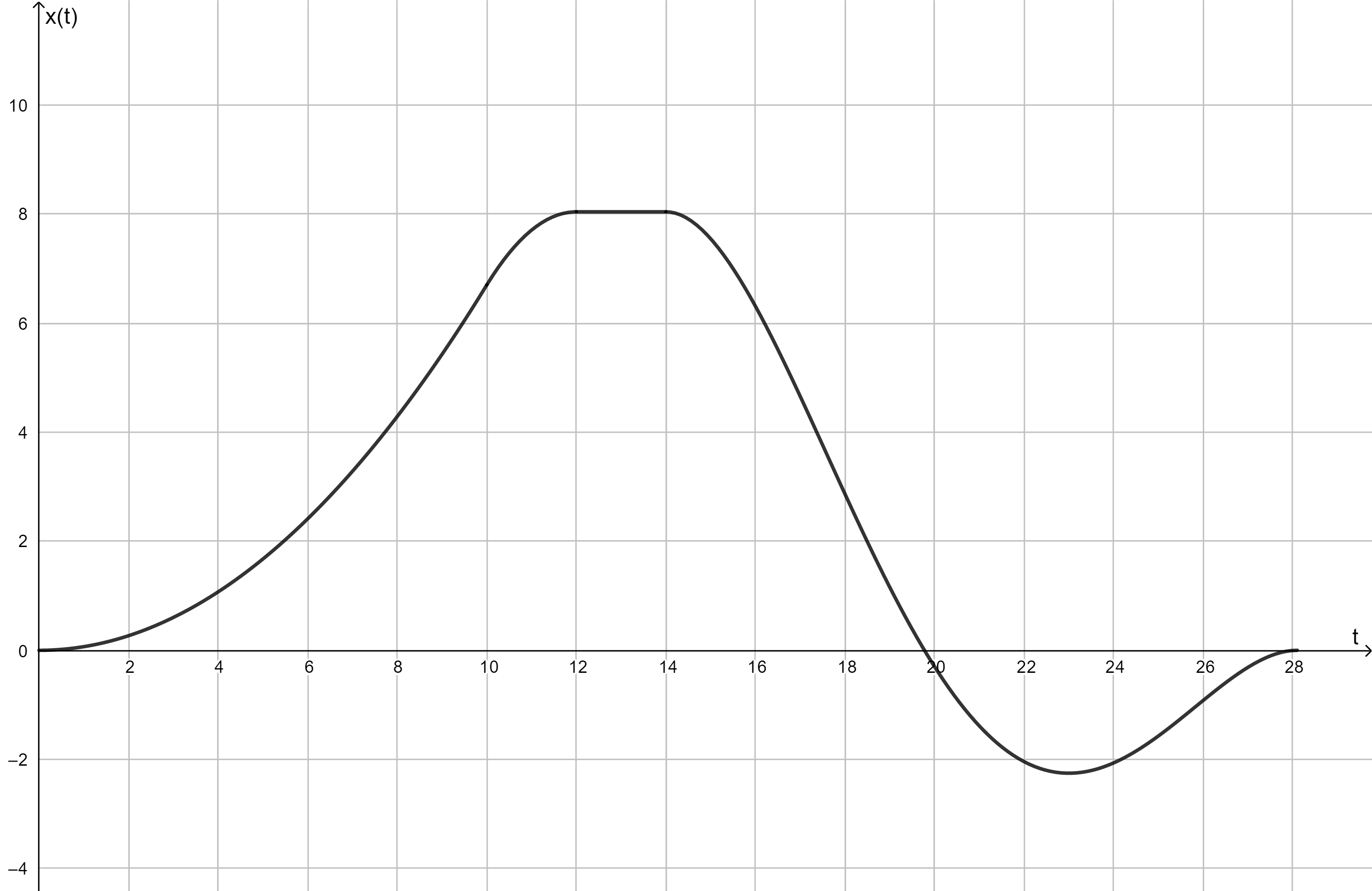 Nr. 4442
|
|
|---|---|
| Lösungsweg | |
NEWS
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!