Fragenliste von Schwerpunkt

Gegeben sind zwei Massen (\(m_1=m_2\)) mit den jeweiligen Ortsvektoren \(\vec{x}_1 = \left( \begin{array}{c} 5 \\\ 1 \\\ \end{array}\right)\) und \(\vec{x}_2 = \left( \begin{array}{c} 1 \\\ 3 \\\ \end{array}\right)\). Wie lauten die Koordinaten des gemeinsamen Massenmittelpunkts \(\vec r_S\)? Fertige eine Skizze an. Nr. 4445
	\(\vec r_S = \begin{pmatrix} 3\\2 \end{pmatrix}\)
	\(\vec r_S = \begin{pmatrix} 6\\4 \end{pmatrix}\)
	\(\vec r_S = \frac{\begin{pmatrix} 3\\2 \end{pmatrix}}{(m_1 + m_2) }\)
	\(\vec r_S = (m_1 + m_2) \cdot \begin{pmatrix} 3\\2 \end{pmatrix}\)
	\(\vec r_S = \begin{pmatrix} 2\\-1 \end{pmatrix}\)
Lösungsweg Die beiden Massen sind in folgendem Diagramm eingezeichnet. Der Massenmittelpunkt zweier Massen \(m_1\) und \(m_2\) ist definiert durch: \(\vec r_S=\frac{\sum_{i=1}^{2}m_i\cdot \vec r_i}{M_{ges}} = \frac{m_1\cdot \vec r_1 + m_2\cdot \vec r_2}{m_1 + m_2}\) Da beide Massen gleich groß sind (\(m_1=m_2\)), muss der Massenmittelpunkt in der Mitte der Verbindungslinie zwischen den Orten der beiden Massen liegen. Eine geometrische Lösung wäre, vom Ort der Masse \(m_2\) (oder auch \(m_1\)) aus die Hälfte der Strecke in x- und y-Richtung zu gehen. Dabei bezeichnen \(\Delta x\) und \(\Delta y\) die Abstände in x- und y-Richtung der beiden Orte, an denen sich die jeweiligen Massen befinden (siehe Graphik). \(\vec r_2 +\frac{1}{2}\cdot \vec{r_2 r_1} = \vec r_2 + \frac{1}{2} \left( \vec r_1 - \vec r_2 \right)=\)\(\,\begin{pmatrix} 5\\1 \end{pmatrix} + \frac{1}{2}\cdot \left[ \begin{pmatrix} 1\\3 \end{pmatrix} - \begin{pmatrix} 5\\1 \end{pmatrix} \right] = \)\(\, \begin{pmatrix} 5\\1 \end{pmatrix} +\begin{pmatrix} -2\\1 \end{pmatrix} = \begin{pmatrix} 3\\2 \end{pmatrix}\) Das führt zum selben Ergebnis wie die Berechnung mittels obiger Formel: \(\vec r_S= \frac{m\cdot\, ( \vec x_1 +\vec x_2)}{2m} = \frac{1}{2}\cdot\, \left[ \begin{pmatrix} 5 \\ 1 \\\end{pmatrix} + \begin{pmatrix}1 \\ 3 \end{pmatrix} \right]\) \(\vec r_S = \begin{pmatrix} 3\\2 \end{pmatrix}\)

Ein Behälter mit Höhe \(h=10\, cm\) wird bis zur Hälfte mit Wasser gefüllt. Daraufhin wird Benzin dazu geleert, bis der Behälter voll ist. Da Benzin und Wasser (kaum) ineinander lösbar sind, schwimmt das Benzin am Wasser auf. Auf welcher Höhe \(h_S\) befindet sich der Schwerpunkt dieses gefüllten Behälters? (Die Masse des Behälters selber wird dabei vernachlässigt.) Die Dichten von Wasser und Benzin sind: \(\rho_{W}=1,0\ \frac{kg}{l}\), \(\rho_{B}=0,75\ \frac{kg}{l}\) Nr. 4446
	\(h_S = 5\, cm\)
	\(h_S \quad \approx \quad 5,4\, cm\)
	\(h_S \quad \approx \quad 3,75\, cm\)
	\(h_S \quad \approx \quad 4,6\, cm\)
	\(h_S \quad \approx \quad 4,2\, cm\)
Lösungsweg Um den gemeinsamen Schwerpunkt der beiden Flüssigkeiten zu ermitteln, werden diese zunächst durch ihre Massenmittelpunkte (MMP) beschrieben. Dadurch werden die beiden ausgedehnten Flüssigkeiten als Punktmassen im jeweiligen MMP angenommen, deren Massen der der Flüssigkeit entsprechen. Es wurde also das Problem auf ein System aus zwei Massen reduziert, das wir nun lösen wollen. Die Form des Behälters ist nicht näher beschrieben, wir können also eine eindimensionale Beschreibung - entlang der Höhe des Behälters - wählen (dabei gehen wir davon aus, dass sich der Querschnitt des Behälters mit der Höhe nicht ändert). Die Flüssigkeiten sind in ihrer Hälfte des Behälters homogen verteilt, die Koordinaten der MMP des Wassers und des Benzins müssen daher \(S_W=\frac{1}{4}h\) und \(S_{B}=\frac{3}{4}h\) sein (siehe Graphik). Die Massen der beiden Flüssigkeiten verhalten sich zueinander genauso wie deren Dichten \(\rho_{W}=1,0\ \frac{kg}{l}\) und \(\rho_{B}=0,75\ \frac{kg}{l}\), da die beiden Flüssigkeiten das selbe Volumen einnehmen. Mit \(M=\rho \cdot V\) gilt also: \(\frac{M_B}{M_{W}} = \frac{\rho_B\cdot V}{\rho_W\cdot V} = \frac{0,75}{1,0}\) beziehungsweise \(M_B = 0,75 \; M_W\). Nun kann in die bekannte Formel für den MMP eingesetzt werden: \(S=\frac{m_W\cdot S_W + m_B\cdot S_B}{m_W + m_B} = \frac{m_w\cdot \frac{1}{4}\,h + 0,75\,m_W\cdot \frac{3}{4}\,h}{m_W + 0,75\,m_W}\) \(=\frac{\cancel{m_W}\cdot h\cdot\, (0,25 +0,75\cdot 0,75)}{1,75\,\cancel{ m_W}} \quad \approx \quad 0,4643\,h\) Die Höhe beträgt \(10\, cm\), daher liegt der gemeinsame MMP der beiden Flüssigkeiten bei \(S\quad \approx \quad 4,6\,cm\)

Aus der linken obere Ecke einer planparallelen rechteckigen Platte mit den Seitenlängen \(a_1=6\,cm\) und \(b_1=9\,cm\) wird ein Rechteck mit Seitenlängen \(a_2 = 2\,cm\) und \(b_2 =3\,cm\) herausgeschnitten. Setze dabei den Koordinatenursprung in die linke untere Ecke, wie in der Graphik dargestellt. Wie sind die x- und y-Koordinaten des Massenmittelpunkts dieser Platte? 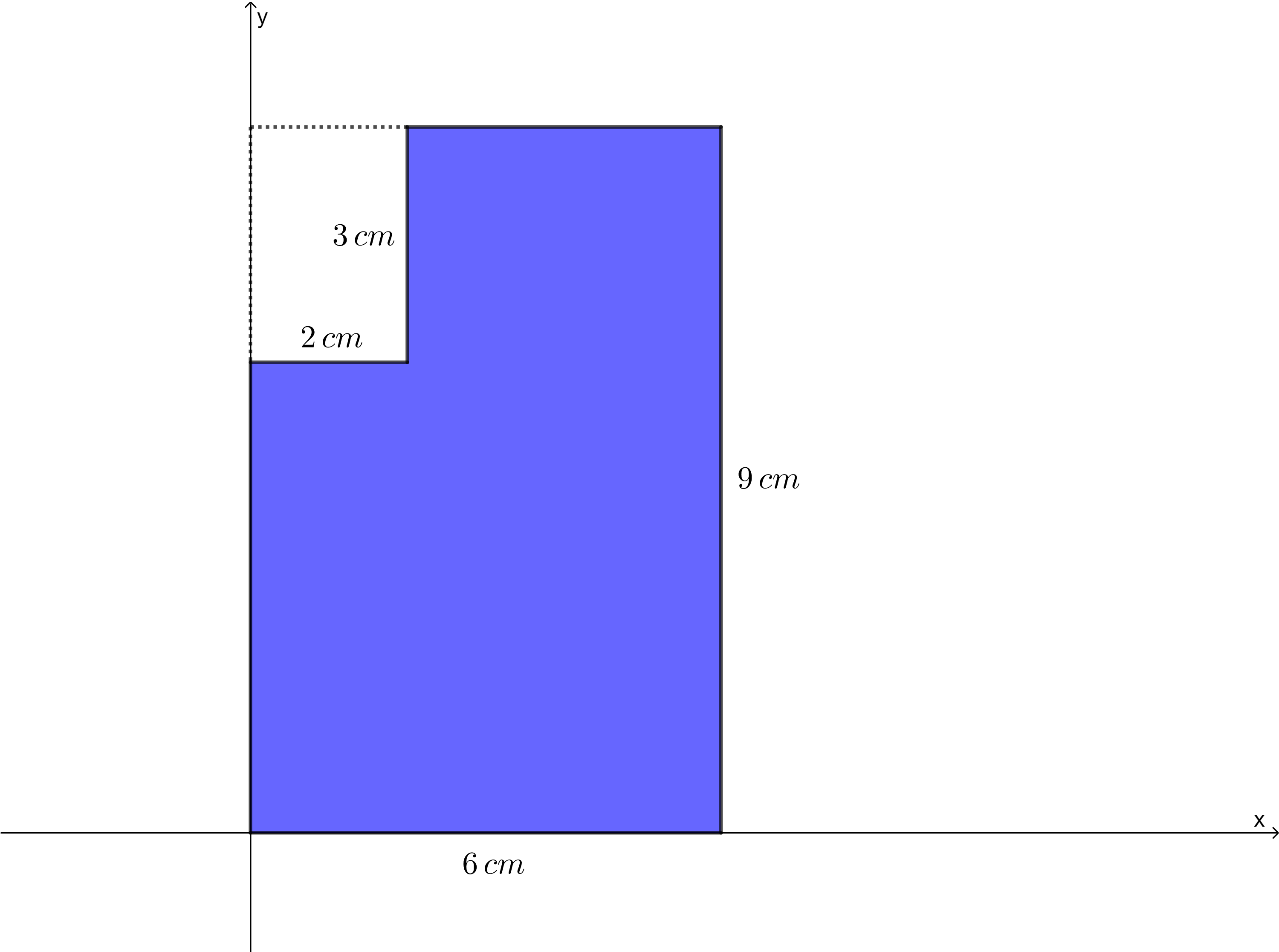Nr. 4447
	\(\vec S=\begin{pmatrix} 2,75\\4,875 \\\end{pmatrix}\)
	\(\vec S=\begin{pmatrix} 3,5\\5,25 \\\end{pmatrix}\)
	\(\vec S=\begin{pmatrix}3,25\\ 4,125 \end{pmatrix}\)
	\(\vec S=\begin{pmatrix}3,5\\ 4,25 \end{pmatrix}\)
	\(\vec S=\begin{pmatrix}2,75\\ 4,125 \end{pmatrix}\)
Lösungsweg Um den Massenmittelpunkt (MMP) der resultierenden Platte zu bestimmen, wird diese zunächst in zwei Flächen unterteilt. Da wir davon ausgehen, dass die Masse der Platte homogen verteilt ist (was bei planparallelen Platten meist der Fall ist), werden die beiden Flächen als Punktmassen betrachtet, die in den jeweiligen Massenmittelpunkten liegen. Dadurch wird die Massenverteilung als Zweikörper-Problem beschrieben und der gemeinsame MMP der beiden Punktmassen entspricht dem MMP der gesamten Platte. Bei geschickter Wahl dieser Teilflächen können die Koordinaten der MMP aus Symmetrie-Überlegungen bestimmt werden. Eine mögliche Wahl wäre die Unterteilung der Form in zwei Rechtecke, wie in der Graphik dargestellt. Die Unterteilung in Rechtecke ist naheliegend, da der MMP eines Rechtecks (bei homogener Massenverteilung) im Schnittpunkt der Diagonalen liegt. In der Graphik sind die beiden Flächen farbig unterlegt und ihre jeweiligen MMP als \(S_1\) und \(S_2\) bezeichnet. (Eine Andere Wahl der Flächen wäre genauso möglich, ebenso eine Unterteilung in mehr als zwei Teilflächen --> Bonusaufgabe!) Der gemeinsame MMP muss dann auf der Verbindungslinie zwischen den beiden Schwerpunkten \(S_1\) und \(S_2\) liegen. Der MMP einer diskreten Massenverteilung, wie wir sie modelliert haben, ist definiert als: \(\vec S = \frac{m_1 \cdot \vec s_1 + m_2 \cdot \vec s_2}{m_1 + m_2}\) Wobei \(\vec s_1\) und \(\vec s_2\) die Ortsvektoren der MMP der beiden Teilflächen sind. Die Koordinaten dieser Ortsvektoren lassen sich aus geometrischen Überlegungen bestimmen. Die MMP ergeben sich durch Halbieren der Seitenlängen der jeweiligen Teilflächen. Dadurch ergeben sich (siehe Graphik): \(\vec s_1 = \begin{pmatrix} 3\\3\\ \end{pmatrix} \qquad , \qquad \vec s_2 = \begin{pmatrix} 4\\7,5\\ \end{pmatrix}\) Da es sich um eine homogene Massenverteilung in der planparallelen Platte handelt, ist das Verhältnis der jeweiligen Massen der Teilflächen gleich dem Verhältnis ihrer Flächeninhalte. Die Dicke \(d\) der Platte ist nicht näher spezifiziert, da es sich aber um eine planparallele Platte handelt, muss \(d=const.\) gelten. Die Masse würde sich berechnen durch \(m_i = \rho \cdot V_i \qquad\qquad \qquad(i=1,2)\), wobei das Volumen \(V_i = a_i \cdot b_i \cdot d\) ist. Für das Verhältnis der Massen gilt \(\frac{m_1}{m_2} = \frac{\cancel{\rho}\cdot a_1\cdot b_1 \cdot \cancel{d}}{\cancel{\rho} \cdot a_2 \cdot b_2 \cdot \cancel{d}} = \frac{a_1\cdot b_1}{a_2\cdot b_2} = \frac{A_1}{A_2}\), es lassen sich also die Massen der Teilflächen durch deren Flächeninhalte ausdrücken. Somit ergibt sich für den gemeinsamen MMP der Punktmassen und damit den MMP der Platte: \(\vec S = \frac{A_1\cdot \vec s_1 + A_2 \cdot \vec s_2}{A_1 + A_2} = \frac{6\cdot6\cdot\, \begin{pmatrix} 3\\3\\ \end{pmatrix} + 4\cdot 3\cdot\, \begin{pmatrix} 4\\ 7,5\\ \end{pmatrix}}{36+12} =\)\(\frac{1}{48}\cdot\,\left[36\cdot\, \begin{pmatrix} 3\\3\\ \end{pmatrix} + 12\cdot\, \begin{pmatrix} 4\\ 7,5\\ \end{pmatrix}\right] = \frac{1}{48}\cdot\, \begin{pmatrix} 156\\198\\ \end{pmatrix}\) \(\vec S=\begin{pmatrix}3,25\\ 4,125 \end{pmatrix}\)

Aus einer quadratischen Holzplatte mit Seitenlänge \(a=50\,cm\) wird ein Kreis mit Radius \(r=5\, cm\) geschnitten. Wird der Ursprung des Koordinatensystems in die linke untere Ecke der Holzplatte gelegt, so liegt der Mittelpunkt des ausgeschnittenen Kreisstückes bei \(M_r=\left( 40/10 \right)\) (siehe Graphik). Wo ist der Schwerpunkt dieser Holzplatte? 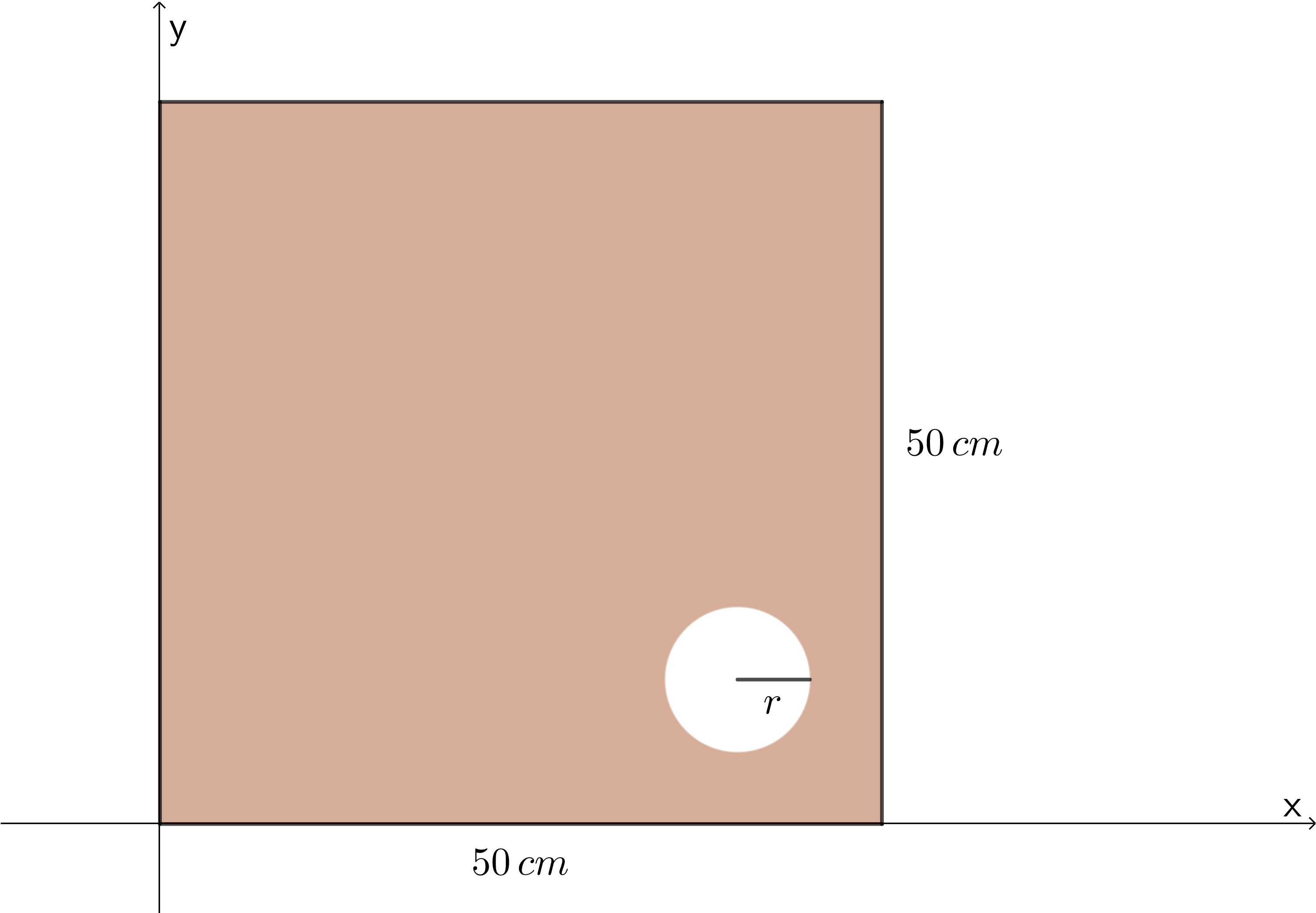Nr. 4448
	\(S = \left( 24,5 / 25,5 \right)\)
	\(S = \left( 32,5 / 17,5 \right)\)
	\(S = \left( 23 / 27 \right)\)
	\(S = \left( 22,75 / 27,25 \right)\)
	\(S = \left( 24,5 / 24,5 \right)\)
Lösungsweg Um den Massenmittelpunkt (MMP) der Holzplatte zu bestimmen, stellen wir zunächst die Flächen durch deren Massenmittelpunkte dar. Der MMP der unbeschnittenen Holzplatte liegt im Schnittpunkt der beiden Diagonalen des Quadrats bzw. werden die Seitenlängen halbiert - das führt zu \(S_{ges} = \left( 25/25 \right)\). Der MMP der Kreisfläche liegt genau im Mittelpunkt des Kreises, also: \(S_{K} = \left( 40/10 \right)\). Gesucht ist der MMP der Platte mit ausgeschnittenem Kreis, den wir \(S_{P}\) nennen wollen. Indem wir die homogenen Flächen (homogen, weil die Masse innerhalb der Platte gleichmäßig und kontinuierlich verteilt ist) durch deren MMP ausdrücken, können wir die Lösung der Aufgabe auf ein diskretes zwei-Körper-Problem zurückführen. Wir teilen die gesamte Plattenfläche in die Fläche der ausgeschnittenen Platte und der Kreisfläche, wie graphisch dargestellt. Dann muss für den MMP der unbeschnittenen Platte gelten: \(S_{ges} = \frac{m_{P}\cdot S_{P} + m_{K}\cdot S_{K}}{m_{P} + m_{K}\) Wobei \(m_P\) die Masse der Platte mit Loch und \(m_K\) die Masse des ausgeschnittenen Kreisstückes sind. Gesucht ist nun der MMP der Platte ohne der Kreisfläche! Umformen: \(S_{ges}\cdot (m_P+m_K) = m_{P}\cdot S_{P} + m_{K}\cdot S_{K} \quad\Rightarrow\quad S_P= \frac{S_{ges}\cdot\, (m_P+m_K)-m_{K}\cdot S_{K}}{m_P}\) Da aber gelten muss: \(m_{ges} = m_P+m_K\) und damit \( m_P = m_{ges} - m_K \) lässt sich schreiben: \(S_P= \frac{ m_{ges}\cdot S_{ges}-m_{K}\cdot S_{K}}{m_{ges} - m_K}\) Man zieht in der Formel für den MMP also die ausgeschnittene Fläche ab, anstatt sie zu addieren! Da die Massen zwar nicht berechnet werden können, aber dafür direkt proportional zu den jeweiligen Flächen sind, können in der Formel die Massen durch die Flächeninhalte ersetzt werden. Das führt schließlich zu: \(S_P = \frac{50\cdot 50\cdot\, \begin{pmatrix} 25\\25\\ \end{pmatrix} - \pi\cdot r^2 \cdot\, \begin{pmatrix}40\\10\\ \end{pmatrix}}{50\cdot 50 - \pi\cdot r^2} =\)\(\quad \frac{1}{2500-25\pi}\cdot \begin{pmatrix} 62500 - 1000\pi \\ 62500 - 250\pi \end{pmatrix} = \begin{pmatrix} 24,5\\25,5 \end{pmatrix}\) Alternativer Lösungsweg: Die Platte kann ebenso in mehrere Teilflächen geteilt werden, von denen der MMP jeweils geometrisch leicht bestimmt werden kann. Hier gibt es verschiedene Ansätze, ein möglicher ist in der Graphik rechts dargestellt: Dabei sind die beiden grün unterlegten Flächen gleich groß. Die blaue Fläche ergibt sich, indem ein Quadrat um den ausgeschnittenen Kreis gelegt wird. Die Masse bzw. Fläche des Kreises muss dementprechend abgezogen werden, der MMP des Quadrates liegt allerdings wiederum im Mittelpunkt des Kreises. Die Lösung auf diese Weise bleibt an dieser Stelle eine Bonusaufgabe!

Auf einem homogenen Stab der Länge \(l=5\) liegen 3 Massen, wie in der Graphik angeordnet: \(m_1\) am Ort \(x_1=1\), \(m_3\) am Ort \(x_3=3\) und \(m_4\) am Ort \(x_4=4\). Dabei gilt: \(m_3=m_1\) und \(m_4 = 2\cdot m_1\) Welche Masse muss ein viertes Gewicht am Ort \(x_2=2\) haben, damit der Schwerpunkt genau in der Mitte (in x-Richtung) des Stabes liegt, wenn \(m_1=3\,kg\)? 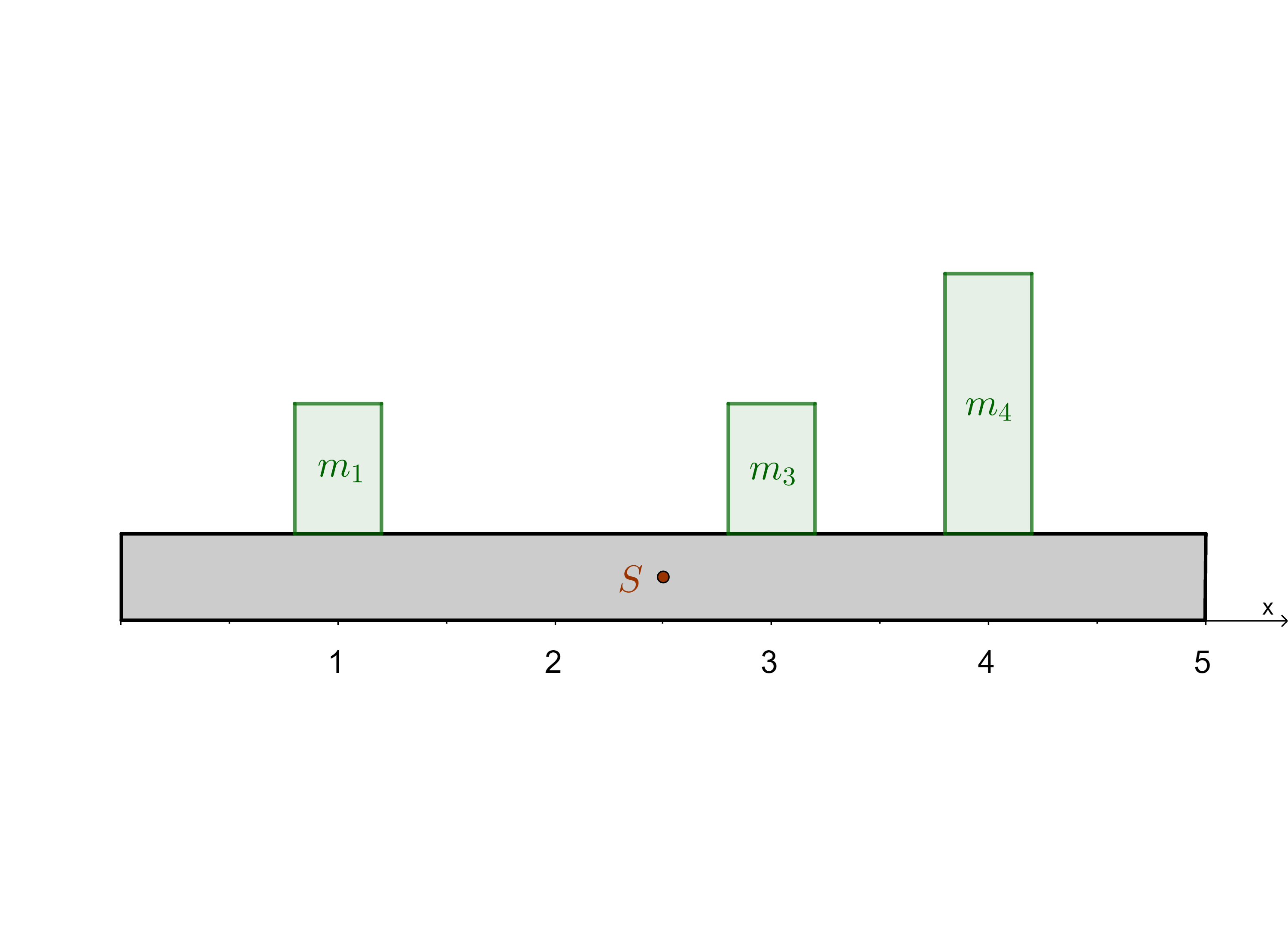Nr. 4449
	\(m_2=6\, kg\)
	\(m_2=12\, kg\)
	\(m_2=9\, kg\)
	\(m_2=24\, kg\)
	\(m_2=7,5\, kg\)
Lösungsweg Für eine diskrete eindimensionale Massenverteilung ist der Massenmittelpunkt definiert als: \(S= \frac{\displaystyle\sum_{i=1}^{n}m_i\cdot x_i}{\displaystyle\sum_{i=1}^{n}m_i}\) Einsetzen der gegebenen Orte und Massen ergibt: \( S = \frac{m_1\cdot x_1+m_2\cdot x_2+m_3\cdot x_3+m_4\cdot x_4}{m_1+m_2+m_3+m_4}=\frac{m_1+2\cdot m_2 + 3\cdot m_1 + 4\cdot 2\cdot m_1}{m_1+m_2+m_1+2\cdot m_1}\)\(\,=\frac{12m_1+2m_2}{4m_1 + m_2} = \frac{l}{2}=2,5\) Diese Gleichung muss nun noch nach \(m_2\) umgeformt werden: \(\frac{12m_1+2m_2}{4m_1 + m_2} =2,5 \qquad \qquad \qquad /\cdot (4m_1+m_2)\) \(12m_1 +2m_2 = 10m_1+2,5m_2 \qquad \Rightarrow \qquad 0,5m_2 = 2m_1\) \(m_2 = 4\cdot m_1\) Es muss also die Masse \(m_2\) vier mal so groß sein wie die Masse \(m_1\)! Da \(m_1=3\,kg\) ist \(m_2=12\,kg\).

Ein Drehkran wird mit folgenden Kräften belastet: Höchstlast \(F=8\,kN\), Eigengewichtskraft \(F_E=6\,kN\) und der Gegengewichtskraft \(F_G=12\,kN\). Die Abstände betragen \(l_1=5,5\,m\), \(l_2=1\,m\) und \(l_3=1,5\,m\). Wie groß ist der Abstand \(l_0\) der Resultierenden \(F_r\) der drei Kräfte von der Drehachse, die durch Punkt A verläuft? Nr. 4462
	\(l_0\quad \approx \quad 1,54\,m\)
	\(l_0\quad \approx \quad 2,92\,m\)
	\(l_0\quad \approx \quad 2,50\,m\)
	\(l_0\quad \approx \quad 1,23\,m\)
	\(l_0\quad \approx \quad 1,88\,m\)
Lösungsweg Da die drei Kräfte parallel zueinander stehen, ist die Resultierende die Summe der einzelnen Kräfte (die Gesamtgewichtskraft): \(F_r=\left\| \vec F_r\right\| = F_G+F_E+F=26\,kN\) Um die Lage der Resultierenden - also den Schwerpunkt - zu bestimmen, verwenden wir die Tatsache, dass dort die Summe der Drehmomente verschwinden muss. Wie aus der Graphik ersichtlich, wird bei der links angreifenden Gegenkraft \(F_G\) der Hebelarm von \(l_3\) auf \(l_3 + l_0\) verlängert, während die Hebelarme der anderen beiden Kräfte jeweils um \(l_0\) verkürzt werden. Anmerkung: dass sich die Resultierende tatsächlich auf der rechten Seite des Punktes A befindet, muss nicht zwingend der Fall sein. Sollte er auf der linken Seite liegen, bekämen wir einen negativen Wert für \(l_0\). Mit der üblichen Vorzeichenkonvention - positives Vorzeichen für Drehmomente gegen den Uhrzeigersinn und negatives für Drehmomente im Uhrzeigersinn - erhalten wir: \(F_G\cdot (l_3+l_0) = F_E\cdot (l_2-l_0) + F\cdot (l_2+l_1 - l_0)\) \(F_G\cdot l_3 + F_G\cdot l_0 = F_E\cdot l_2-F_E\cdot l_0 + F\cdot (l_2 + l_1) - F\cdot l_0 \hspace{18mm} \| \qquad l_0\ \mathrm{herausheben}\) \(l_0\cdot ( \underbrace{F_G + F_E + F}_{F_r} )= F_E\cdot l_2 + F\cdot (l_2 + l_1)-F_G\cdot l_3\) \(\Rightarrow \qquad l_0=\frac{F_E\cdot l_2 + F\cdot (l_2 + l_1)-F_G\cdot l_3}{F_r} = \quad\)\(\frac{6\,kN\cdot 1\,m + 8\,kN\cdot 6,5\,m - 12\,kN\cdot 1,5\,m}{26\,kN} = \frac{40\,kNm}{26\,kN}\qquad \approx \qquad 1,54\,m\) Alternativer Lösungsweg: Ein anderer und wesentlich kürzerer Lösungsweg wäre gewesen, die Schwerpunktformel zu verwenden und dabei die Drehachse bzw. den Punkt A in den Ursprung zu setzen. Interpretieren wir den Kran mit den wirkenden Kräften als System aus drei Massenpunkten, wird die Rechnung wesentlich einfacher. Für ein System aus \(N\) Massenpunkten lässt sich der Schwerpunkt berechnen mit: \(S=\frac{\displaystyle\sum_{i=1}^N m_i\cdot x_i}{\displaystyle\sum_{i=1}^N m_i}\) Dabei bezeichnen \(x_i\) die Abstände der Punktmassen vom Ursprung des Koordinatensystems. Die Masse lässt sich durch die Gewichtskraft ausdrücken: \(F=m\cdot g \qquad \Rightarrow \qquad m=\frac{F}{g}\) Die Erdbeschleunigung \(g\) kürzt sich allerdings in der Formel für den Schwerpunkt stets heraus, weswegen anstatt der Masse \(m\) in der Formel die Gewichtskraft \(F\) geschrieben werden kann (Bonusaufgabe: dies zu überprüfen!). Wenn der Punkt A in den Ursprung gelegt wird, kommt man durch Einsetzen in die Schwerpunktformel auf die obige Gleichung für \(l_0\): \(l_0=S=\frac{-F_G\cdot l_3 + F_E\cdot l_2 + F\cdot\, (l_2+l_3)}{F_G+ F_E + F}\)

Die abgebildete Waage befinde sich im statischen Gleichgewicht. Wo liegt der Schwerpunkt \(S\)? Für die Massen gelte dabei \(2\,m_2 = m_1\). Die x-Achse wird so gelegt, dass die Koordinate des Schwerpunkts \(x_S\) der Länge \(l_1\) in der Abbildung entspricht. Das Eigengewicht der Waage wird dabei vernachlässigt. 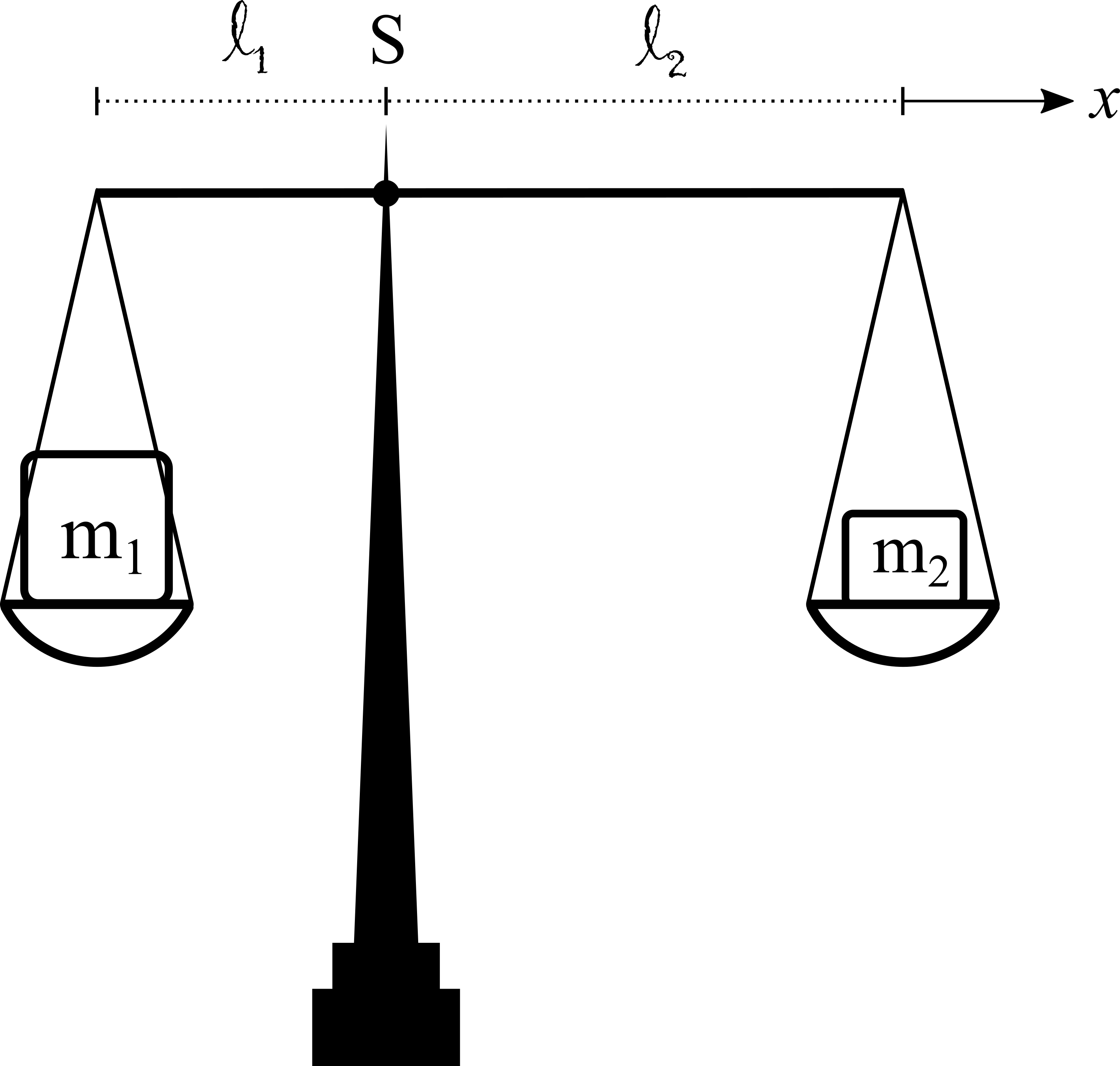Nr. 4475
	\(l_1 = l_2\)
	\(l_1 = \frac{1}{2}\cdot l_2\)
	\(l_1 = 2\cdot l_2\)
	\(l_1 = \frac{m_2}{2}\cdot l_2\)
	\(l_1 = \frac{1}{l_2}\)
Lösungsweg Um die Lage des Schwerpunkts zu bestimmen, geht man bei diesem eindimensionalen Problem am Besten von einem Drehmomenten-Ansatz aus: Wir legen die Drehachse, wie abgebildet, so, dass sie den Schwerpunkt enthält. Das Drehmoment im Schwerpunkt muss dann 0 ergeben. Wie in der Abbildung zu sehen, bewirkt die Masse \(m_1\) eine Rotation gegen den Uhrzeigersinn, konventionsgemäß ein positives Drehmoment. Demenstprechend erhält das Drehmoment der Masse \(m_2\) ein negatives Vorzeichen. Das Drehmoment ist definiert als: \(M = \displaystyle\sum_i G_i \cdot l_i\) Dabei bezeichnen \(G_i\) die Gewichtskräfte der Massen und \(l_i\) deren Hebelarme - die senkrechten Abstände der Wirklinie der Gewichtskraft zur Drehachse. Mit der Schwerebeschleunigung auf der Erde \(g = 9,81\,\frac{m}{s^2}\) lässt sich die Gewichtskraft der Massen berechnen: \(G_i = m_i \cdot g\). Da sich das netto-Drehmoment im Schwerpunkt zu Null addiert, erhalten wir: \(M = G_1 \cdot m_1 - G_2 \cdot m_2 = 0\) \(m_1 \cdot \cancel{g} \cdot l_1 = m_2 \cdot \cancel{g} \cdot l_2 \qquad \Rightarrow \qquad l_1 = \frac{m_2}{m_1}\cdot l_2\) Mit \(m_1 = 2\cdot m_2\) erhalten wir schließlich: \(l_1= \frac{\cancel{m_2}}{2\cdot \cancel{m_2}}\cdot l_2 = \frac{1}{2}\cdot l_2\)

Welche Aussage(n) über den Schwerpunkt eines starren Körpers ist/sind korrekt? Nr. 4477
	Schwerpunkt und Massenmittelpunkt sind äquivalente Ausdrücke.
	Der Schwerpunkt befindet sich stets an dem Ort, an dem die Massendichte \(\rho(\vec r)\) ein Maximum hat.
	Der Schwerpunkt eines starren Körpers kann sich auch außerhalb des Volumens befinden, das der Körper einnimmt.
	Bei symmetrischen Körpern ist der Schwerpunkts stets ein Teil des Körpers.
	Der Schwerpunkt ist ein ausgezeichneter Punkt - das heißt, ein Körper oder ein System aus Massenpunkten kann nicht mehrere Schwerpunkte gleichzeitig besitzen.
Lösungsweg Antworten 3) und 5) sind korrekt! ad 3) Der Schwerpunkt eines starren Körpers kann sich auch außerhalb des Volumens befinden, das der Körper einnimmt. Beispielsweise liegt der (Flächen-)Schwerpunkt eines Kreises in dessen Mittelpunkt. Wird aus dem Kreis ein kleinerer herausgeschnitten, sodass die Mittelpunkte der beiden Kreise am selben Ort sind, so ist der Schwerpunkt immer noch im Mittelpunkt der beiden Kreise. Das herausgeschnittene Stück ist aber kein Teil des Körpers mehr und so befindet sich der Schwerpunkt außerhalb des Volumens des Körpers. Das ist in der Abbildung verdeutlicht, der Schwerpunkt ist rot dargestellt. ad 5) Der Schwerpunkt ist ein ausgezeichneter Punkt - das heißt, ein Körper oder ein System aus Massenpunkten kann nicht mehrere Schwerpunkte gleichzeitig besitzen. Ein Körper kann mehrere Symmetrieachsen besitzen. Wenn mehrere Symmetrieachsen vorhanden sind, dann liegt der Schwerpunkt stets im Schnittpunkt dieser Symmetrieachsen. Bei nicht symmetrischen Körpern liegt der Schwerpunkt im Schnittpunkt der Schwerelinien, den Wirklinien der Gewichtskräfte. Die Symmetrieachsen wie auch Schwerelinien treffen alle in einem Punkt, dem Schwerpunkt, zusammen.

Bei welchen dieser homogenen Flächen ist der Schwerpunkt kein Teil der Fläche? (Anmerkung: Es muss nichts berechnet, sondern argumentiert werden.) Nr. 4480
	a)
	b)
	c)
	d)
	e)
Lösungsweg Antworten c) & d) sind korrekt! ad c) Wie in der Abbildung zu sehen, lässt sich die Fläche in zwei Teilflächen zerlegen (andere Einteilungen sind ebenso zulässig). Die Schwerpunkte der Teilflächen sind mit \(M_1\) und \(M_2\) gekennzeichnet. Der gemeinsame Schwerpunkt muss auf der gemeinsamen Verbinungsgeraden liegen und zwar näher an der Fläche mit größerem Flächeninhalt. Die beiden Teilflächen sind annähernd gleich groß, zumindest ist der Unterschied nicht derart groß, als dass der Schwerpunkt innerhalb der Flächen liegen kann. Der Schwerpunkt muss innerhalb des rot gekennzeichneten Bereichs (auf der Verbindungsgeraden!) liegen. ad d) Der Schwerpunkt von Dreiecken liegt auf 1/3 der Seitenhöhe. Aus einem Dreieck wird ein kleineres, dazu ähnliches, herausgeschnitten, sodass quasi nur ein Rand des Dreiecks übrig bleibt. Dieser Rand ist nicht dick genug, sodass der Schwerpunkt beinhaltet sein kann. Abschließend soll noch diskutiert werden, warum der Schwerpunkt bei Aufgabe a) ein Teil der Fläche sein muss: In der Abbildung sind der große Kreis und der kleinere, ausgeschnitte Kreis mit deren Schwerpunkten \(M_1\) und \(M_2\) abgebildet. Der Schwerpunkt der Fläche (Kreis + herausgeschnittener kleinerer Kreis) muss auf der Verbindungsgerade liegen, die \(M_1\) und \(M_2\) enthält. Da allerdings ein Teil herausgeschnitten wird, wird sich der Schwerpunkt hin zu dem Teil der Fläche verschieben, wo mehr Fläche vorhanden ist. Dieser Bereich ist in der Grafik als strichlierte Linie gekennzeichnet. Da bereits der Schwerpunkt des vollen Kreises nicht im ausgeschnittenen Teil liegt (also Teil der Fläche ist), muss der Schwerpunkt der resultierenden Fläche innerhalb dieser liegen.

Berechne den Ortsvektor \(\vec{R}\) des Massenmittelpunktes eines Systems von zwei Punktmassen \(m_1=4 \, kg \) und \(m_2= 500 g\) an den Positionen \(\vec{r_1}= \left ( \begin{array}{c} 2 \\ -4 \\ \end{array} \right )\) und \(\vec{r_2}= \left ( \begin{array}{c} -2 \\ 0 \\ \end{array} \right )\). Nr. 4507
	\(\vec{R}= \frac{1}{4.5} \left ( \begin{array}{c} 7 \\ -16 \\ \end{array} \right )\)
	\(\vec{R}= \frac{1}{3.5} \left ( \begin{array}{c} 7 \\ -16\\ \end{array} \right )\)
	\(\vec{R}=4.5 \cdot \, \left ( \begin{array}{c} 7 \\ -16 \\ \end{array} \right )\)
	\(\vec{R}= 3.5 \cdot \, \left ( \begin{array}{c} 9 \\ -16 \\ \end{array} \right )\)
	\(\vec{R}= \frac{1}{4.5} \left ( \begin{array}{c} 9 \\ -16 \\ \end{array} \right )\)
Lösungsweg Der Massenmittelpunkt eines Systems von \(n\) Punktmassen \(m_i\) an den Orten \(x_i\) ist definiert als: \(\displaystyle \vec{R}=\frac{\sum_i m_i \vec{r_i}}{\sum_i m_i}\) Einsetzen ergibt: \(\vec R = \frac{m_1 \cdot \vec r_1 + m_1 \cdot \vec r_1}{m_1 + m_2} =\)\( \frac{4 \cdot\, \left( \begin{array}{c} 2 \\\ -4 \end{array}\right) + 0,5\cdot \,\left( \begin{array}{c} -2 \\\ 0 \end{array}\right)}{4 + 0,5} =\)\( \frac{\left( \begin{array}{c} 8 \\\ -16 \end{array}\right) + \left( \begin{array}{c} -1 \\\ 0 \end{array}\right)}{4,5} = \frac{1}{4,5}\cdot\, \left( \begin{array}{c} 7 \\\ -16 \end{array}\right)\)

Ein homogener Balken der Länge \(l_0 = 1.4\,m\) ist in A gelagert und liegt in B auf einer Mauerkante auf. Die Abmessungen betragen \(l_1 = 1\,m\) und \(l_2 = 0.6\,m\). In welchem Abstand \(l_G\) zum Lagerpunkt A greift die Gewichtskraft des Balkens an? Nr. 4699
	\(l_G = 60\,cm\)
	\(l_G = 36\,cm\)
	\(l_G = 70\,cm\)
	\(l_G = 58\,cm\)
	\(l_G = 50\,cm\)
Lösungsweg Da es sich um einen homogenen Balken handelt, greift die Gewichtskraft \(F_G\) im Schwerpunkt, in der Mitte des Balkens an. Eine mögliche (wenn auch etwas umständliche) Lösung ist die über den Satz des Pythagoras: \(\left(\frac{l_0}{2}\right)^2 = l_G^2 + h_G^2\), wobei \(h_G\) die Höhe bezeichnet, auf der sich der Schwerpunkt des Balkens befindet (siehe Abbildung). Da es sich um ähnliche Dreiecke handelt, müssen deren Seitenverhältnisse gleich sein: \(\frac{l_1}{l_2} = \frac{l_G}{h_G} \qquad \Rightarrow \qquad h_G = \frac{l_G \cdot l_2}{l_1}\) Damit lässt sich auf die gesuchte Länge \(l_G\) umformen (Herleitung siehe ganz unten): \( l_G = \frac{l_0}{2\cdot \sqrt{1 + \left(\frac{l_2}{l_1}\right)^2}}} = \frac{l_0}{2\cdot \sqrt{1 + \left(\frac{0,6\,m}{1\,m}\right)^2}}} = \frac{1,4\,m}{2\cdot \sqrt{1,36}} = 0,600245\,m\) \(l_G \,\approx\, 60\,cm\) Eine etwas kürzere Lösung ist die über Winkelfunktionen: Für den Winkel, in dem der Balken zur Waagrechten gelagert ist, gilt: \(\tan(\alpha) = \frac{l_2}{l_1} \qquad \Rightarrow \qquad \alpha = \arctan\left(\frac{l_2}{l_1}\right) = 30,96^\circ\). Damit entspricht die halbe Länge des Balkens der Hypothenuse (siehe Abbildung). Die gesuchte Länge \(l_G\) ist dann somit \(l_G = \cos(\alpha) \cdot \frac{l_0}{2} = \cos(30,96^\circ) \cdot 0,7\,m = 0,600\,m\) in Übereinstimmung mit der Lösung über den Satz des Pythagoras. Herleitung des Hebelarms \(l_G\) der Gewichtskraft: Aus \(\left(\frac{l_0}{2}\right)^2 = l_G^2 + h_G^2\) und \( h_G = \frac{l_G \cdot l_2}{l_1}\) (siehe oben) wird zunächst: \(\left(\frac{l_0}{2}\right)^2 = l_G^2 + \left( \frac{l_G\cdot l_2}{l_1} \right)^2 = l_G^2 \cdot \left[ 1 + \left(\frac{l_2}{l_1}\right)^2\right]\) (Herausheben!) \(l_G^2 = \frac{\left(\frac{l_0}{2}\right)^2}{1 + \left(\frac{l_2}{l_1}\right)^2}\qquad \Rightarrow \qquad l_G = \frac{l_0}{2\cdot \sqrt{1 + \left(\frac{l_2}{l_1}\right)^2}}}\)

Auf einem Stab der Länge 5 liegen Gewichte wie abgebildet verteilt. An welcher Stelle \(x_S\) befindet sich der Schwerpunkt dieses Systems? Gehen Sie davon aus, dass alle Körper homogen sind und die selbe Masse \(m\) besitzen. Die Masse des Stabes sei dabei vernachlässigbar. 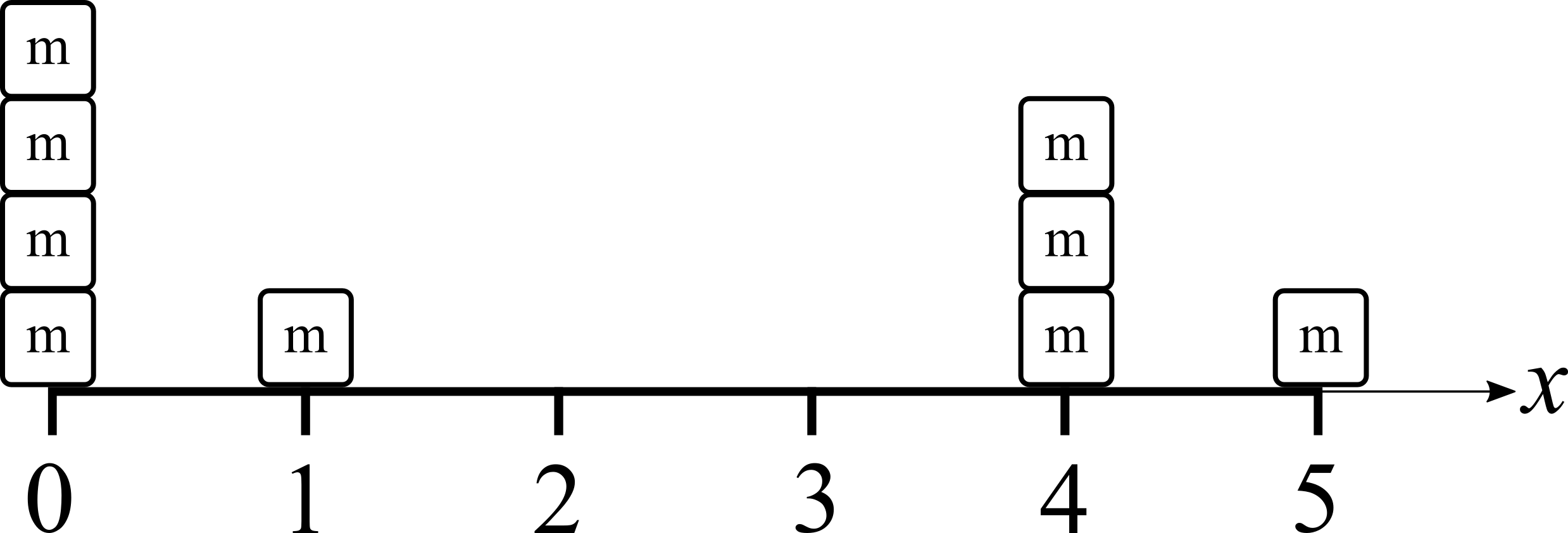Nr. 4728
	\(x_S = 1\)
	\(x_S = 1.5\)
	\(x_S = 2\)
	\(x_S = 2.5\)
	\(x_S = 3\)
Lösungsweg Da es sich um ein 1-dimensionales Problem handelt (es ist nur die x-Koordinate des Schwerpunkts gefragt), kann in die Definitionsgleichung für die x-Koordinate des Schwerpunkts für ein System aus diskreten Massenpunkten eingesetzt werden: \(x_S = \frac{\displaystyle\sum_i m_i\cdot x_i}{\displaystyle\sum_i m_i}\). Dabei bezeichnet \(m_i\) die Masse des i-ten Körpers an der Stelle \(x_i\). Im Nenner steht daher die Gesamtmasse des Systems, \(\displaystyle\sum_i m_i = m_{ges} = 9\). Beispielsweise liegen auf dem Balken an der Stelle \(x = 4\) insgesamt \(3\,m\) an Masse. So ergibt sich: \(x_S = \frac{4\cdot 0 + 1\cdot 1 + 4 \cdot 3 + 1\cdot 5}{4+1+3+1} = \frac{18}{9} = 2\) Anmerkung: Man hätte die Koordinaten des Schwerpunkts auch über den Drehmomenten-Ansatz berechnen können. Beim Schwerpunkt eines solchen Systems ist das netto-Drehmoment \(M = 0\).

Eine einfache Waage besteht aus einem Balken, der in seinem Mittelpunkt drehbar gelagert ist. Die abgebildete Waage hat die Länge 6 und ist mit verschiedenen Gewichten belastet. Um die Waage ins Gleichgewicht zu bringen, ist nur ein weiteres Gewicht der Masse \(m\) nötig. An welcher Stelle \(x_0\) muss das Gewicht platziert werden, sodass die Waage ausgeglichen ist? (Die anderen Gewichte müssen dabei an ihren Plätzen bleiben). 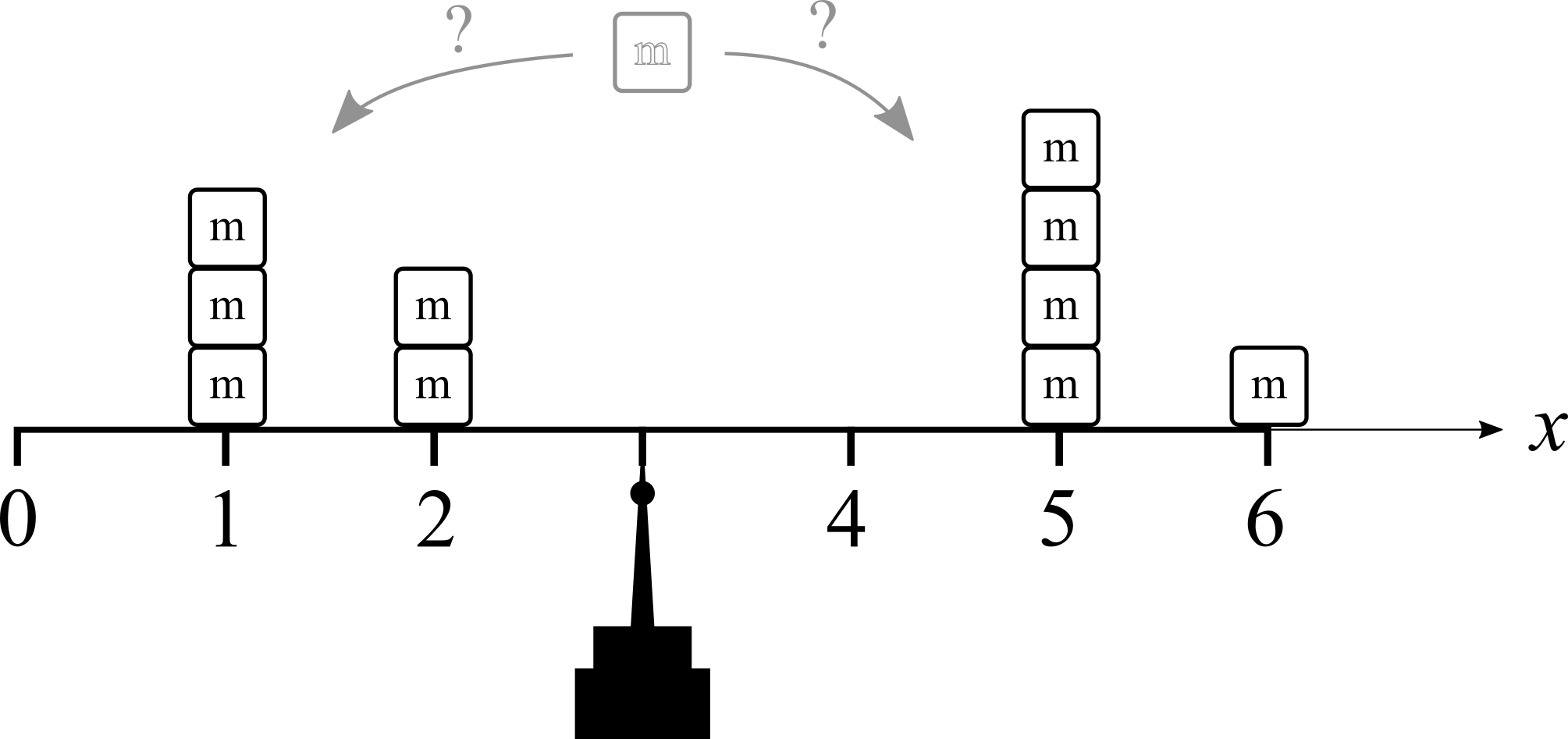Nr. 4729
	\(x_0 = 0\)
	\(x_0 = 1\)
	\(x_0 = 2\)
	\(x_0 = 3\)
	\(x_0 = 4\)
Lösungsweg Lösung Drehmoment: Damit sich die Waage im Gleichgewicht befindet, muss das Drehmoment bezüglich der Drehachse (Lagerpunkt) bei \(x_D=3\) verschwinden. Es müssen also die Gewichtskräfte auf der linken und rechten Seite ein gleich groß entgegengesetztes Drehmoment erzeugen. Nach dem 2. Newtonschen Axiom gilt für die Gewichtskraft eines Körpers der Masse \(m\): \(F_G = m\cdot g\), mit der Erdbeschleunigung \(g\). Das Drehmoment einer Kraft \(F\) ist definiert als \(M = h\cdot F\), wobei \(h\) den Hebelarm der Kraft bezeichnet. Konventionsgemäß ist ein gegen den Uhrzeigersinn drehendes Moment positiv, ein im Uhrzeigersinn drehendes dagegen negativ. Die Abbildung zeigt den Beitrag des Hebelarms zum Drehmoment. In der Mitte (bei \(x_D = 3\)) ist der Hebelarm 0, nach links trägt dieser positiv zum Drehmoment bei, nach rechts hingegen negativ. Damit ergibt sich für das Drehmoment bezüglich der Drehachse in der Mitte des Balkens: \(M = 2\cdot 3\,mg + 1\cdot 2\,mg - 2\cdot 4\,mg - 1\cdot 3\,mg + h_0\cdot mg= 0\) \(6 + 2 - 8 - 3 +h_0 = 0 \qquad \Rightarrow \qquad h_0=3\) Die hinzugefügte Masse \(m\) hat daher den (positiven!) Hebelarm mit Länge 3. Die Position entspricht daher der bei \(x_0 = 0\). Lösung Schwerpunkt: Eine alternative Lösung bietet die Definition des Schwerpunktes: Ist die Waage im Gleichgewicht, so muss der Drehpunkt, an dem das Drehmoment 0 ist, mit dem Schwerpunkt zusammenfallen (sie müssen zumindest den selben x-Wert haben). Anschaulich ist also der Schwerpunkt derjenige Punkt eines Körpers, an dem dieser balanciert werden kann. Die Definition des Schwerpunkts für eindimensionale Probleme: \(x_S = \frac{\displaystyle\sum_i m_i\cdot x_i}{\displaystyle\sum_i m_i}\). (Man erkennt, in dieser Formulierung kommt die Erdbeschleunigung nicht mehr vor!) Da der Schwerpunkt bei \(x_S = x_D = 3\) liegt, muss umgeformt werden. Im nenner steht die Gesamtmasse, bei der die zusätzliche Masse berücksichtigt werden muss:\(\displaystyle\sum_i m_i = m_{ges} = 11\,m\). Einsetzen der gegebenen Koordinaten ergibt: \(x_S = \frac{3\,m\cdot 1 + 2\,m\cdot 2+4\,m\cdot 5 + 1\,m\cdot 6 + 1\,m\cdot x_0}{11\,m} = 3\) \(x_0=3\cdot 11 - (3+4+20+6) = 33 - 33 = 0\) Und wir erhalten das selbe Ergebnis wie über den Ansatz des Drehmoments: \(x_0=0\)

Anmelden

Passwort vergessen
Registrieren

NEWS

Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.

Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support

Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!

https://www.technikum-wien.at/mathe-support/

Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.

Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.

Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.

Anmeldung und Informationen
Warm-up-Kurse

Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!

weitere News

Wussten Sie schon?

Sie können sich rechts oben einen kostenlosen Benutzer erstellen. Dann wird Ihr Lernfortschritt gespeichert, Sie können Tests zwischenspeichern und an Tutorien teilnehmen.

Physik Übungsplattform

Fragenliste von Schwerpunkt

Anmelden

NEWS