
Sie können sich rechts oben einen kostenlosen Benutzer erstellen. Dann wird Ihr Lernfortschritt gespeichert, Sie können Tests zwischenspeichern und an Tutorien teilnehmen.
|
Die konstante Kraft \(\vec{F} = \begin{pmatrix}-12\\1\\3\\\end{pmatrix} \) \(N\) verschiebe einen Massepunkt vom Punkte \(P_1 = (1;-3;4) \) \(m\) aus geradlinig in den Punkt\( P_2 = (0;2;5)\) \(m\). Welche Arbeit wird dabei verrichtet? Wie groß ist der Winkel \(\phi \) zwischen dem Kraft- und dem Verschiebungsvektor? Nr. 2798
|
|
|---|---|
| Lösungsweg | |
|
Die konstante Kraft \(\vec{F} = \begin{pmatrix}4\\8\\0\\\end{pmatrix} \) \(N\) verschiebe einen Massepunkt vom Punkte \(P_1 = (2;-2;4) \) \(m\) aus geradlinig in den Punkt\( P_2 = (1;6;3)\) \(m\). Welche Arbeit wird dabei verrichtet? Wie groß ist der Winkel \(\phi \) zwischen dem Kraft- und dem Verschiebungsvektor? Nr. 2799
|
|
|---|---|
| Lösungsweg | |
|
Elektronen, die mit der Geschwindigkeit \( \vec{v}\) in ein Magnetfeld der Flussdichte \(\vec{B} \) eintreten, erfahren dort die Lorentz-Kraft \(\vec{F_L} = - e (\vec{v} \times \vec{B})\) Wie groß ist die Krafteinwirkung auf ein Elektron, wenn \(\vec{v}\) und \(\vec{B}\) die folgenden Komponenten besitzen? (Elementarladung \(e = 1,6 \cdot 10^{-19}\,C\) )
\(\vec{v} = \begin{pmatrix}1000\\1000\\0\\\end{pmatrix} \,\,\frac{m}{s}\) und \(\vec{B} = \begin{pmatrix}0\\0\\0,2\\\end{pmatrix}\,\,T\) Nr. 2807
|
|
|---|---|
| Lösungsweg | |
|
Ein großes Schiff wird von zwei kleineren gezogen. Das erste Schiff \(B_1\) zieht mit einer Kraft von \(F_1=4000N\) Das zweite Schiff \(B_2\) zieht mit einer Kraft von \(F_2=6000N\) Berechne mit welcher Kraft \(F\) sich das große Schiff (schräg) vorwärts bewegt. Nr. 3540
|
|
|---|---|
| Lösungsweg | |
|
Zwei kleine Schiffe ziehen ein großes hinter sich her. Das erste Schiff \(S_1\) zieht mit einer Kraft von\(F_1=5000N\), während das zweite \(S_2\) mit einer Kraft von \(F_2=13000N\) zieht. Mit welcher Kraft \(F\) wird das große Schiff vorwärts gezogen? Nr. 3541
|
|
|---|---|
| Lösungsweg | |
|
Welche Aussage(n) über ein zentrales Kräftesystem ist/sind korrekt? Nr. 4599
|
|
|---|---|
| Lösungsweg | |
|
In einem zentralen Kräftesystem wirken die Kräfte \(F_1 = 120\,N\), \(F_2 = 210\,N\) und \(F_3 = 90\,N\) unter den jeweiligen Richtungswinkeln \(\alpha_1 = 25^\circ\), \(\alpha_2 = 60^\circ\) und \(\alpha_3 = 170^\circ\). (Der Richtungswinkel \(\alpha\) ist der Winkel, den eine Kraft \(F\) mit einer festgelegten Bezugsachse - üblicherweise die positive x-Achse - einschließt). Berechnen Sie den Betrag der Resultierenden \(F_r\). Nr. 4610
|
|
|---|---|
| Lösungsweg | |
|
In einem zentralen Kräftesystem wirken die Kräfte \(F_1 = 160\,N\) und \(F_2 = 220\,N\), die mit der positiven x-Achse die Winkel \(\alpha_1 = 70^\circ\) und \(\alpha_2 = 160^\circ\) einschließen und mit einer Kraft \(F_3\) im Gleichgewicht stehen. Wie groß ist der Betrag der Kraft \(F_3 = |\vec F_3|\)? In welchem Quadranten wirkt diese Kraft? (Tipp: Skizze!) Nr. 4611
|
|
|---|---|
| Lösungsweg | |
|
An einem starren Körper greifen N Kräftepaare (\(N \qquad \geq \qquad 2\)) an. Der Betrag der i-ten einzelnen Kraft wird als \(F_i\) bezeichnet. Wie groß ist die Resultierende \(F_R\) dieses Kraftsystems? Nr. 4756
|
|
|---|---|
| Lösungsweg | |
|
Auf einen Massenpunkt wirken die vier Kräfte \(\bf{F}_1\), \(\bf{F}_2\), \(\bf{F}_3\) und \(\bf{F}_4\) (die Schreibweise in fetter Schriftstärke stellt Vektoren dar. Diese Schreibweise ist gleichbedeutend mit der Darstellung durch Pfeile). Diese Kräfte bilden ein zentrales Kräftesystem, siehe Abbildung. Wie lautet die Resultierende \(\bf{F}_R\) dieses Kräftesystems? (Die Komponenten des Vektors werden hier mit \(\bf{i}\) und \(\bf{j}\) bezeichnet.) 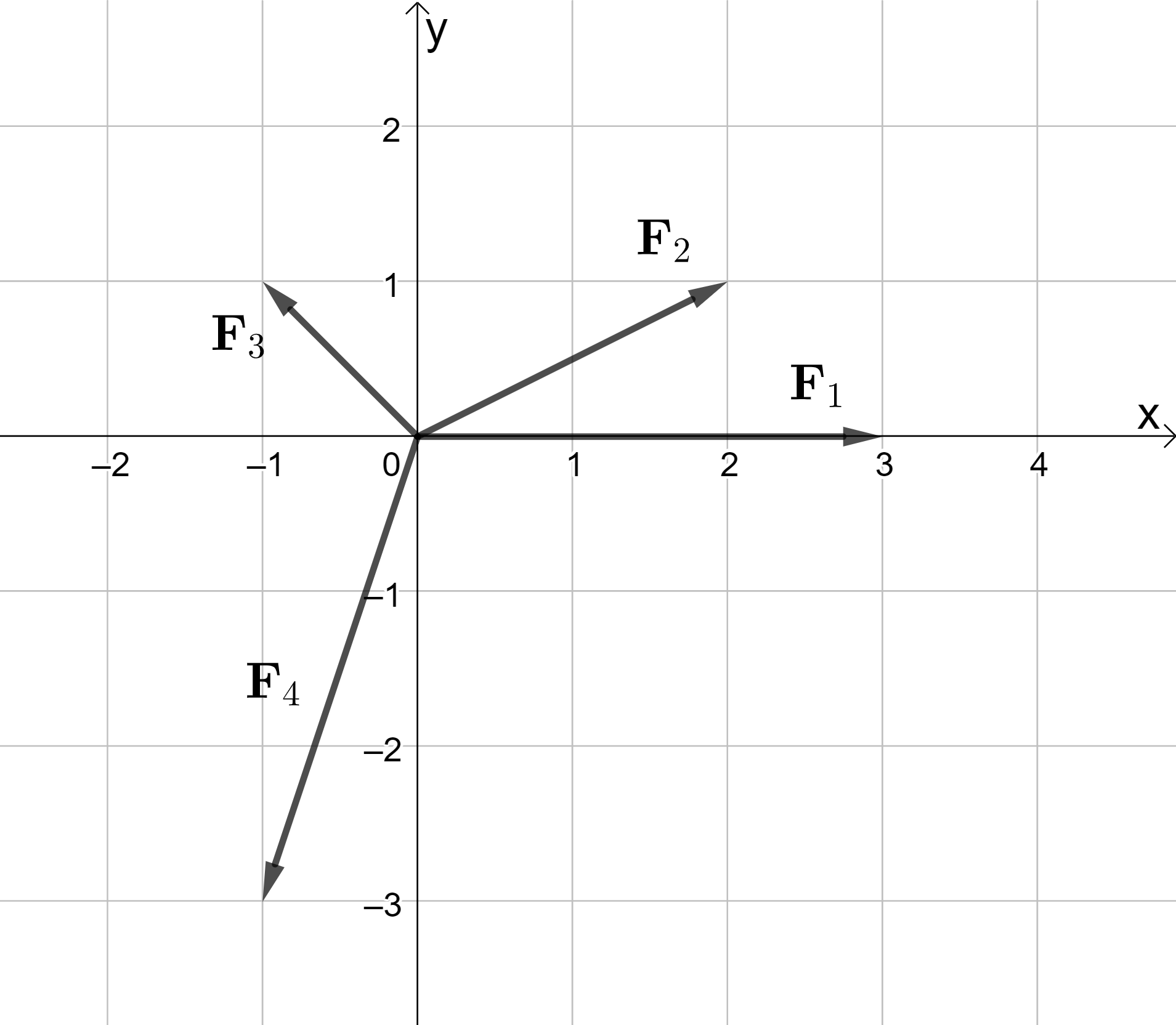 Nr. 4918
|
|
|---|---|
| Lösungsweg | |
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!

Sie können sich rechts oben einen kostenlosen Benutzer erstellen. Dann wird Ihr Lernfortschritt gespeichert, Sie können Tests zwischenspeichern und an Tutorien teilnehmen.