Bei uns können Sie auch reine Mathematik üben: www.mathe.technikum-wien.at
|
Die konstante Kraft \(\vec{F} = \begin{pmatrix}2\\4\\1\\\end{pmatrix} \) \(N\) verschiebe einen Massepunkt vom Punkte \(P_1 = (1;1;1) \) \(m\) aus geradlinig in den Punkt\( P_2 = (1;-3;4)\) \(m\). Welche Arbeit wird dabei verrichtet? Wie groß ist der Winkel \(\phi \) zwischen dem Kraft- und dem Verschiebungsvektor? Nr. 2800
|
|
|---|---|
| Lösungsweg | |
|
Ein Behälter mit Höhe \(h=10\, cm\) wird bis zur Hälfte mit Wasser gefüllt. Daraufhin wird Benzin dazu geleert, bis der Behälter voll ist. Da Benzin und Wasser (kaum) ineinander lösbar sind, schwimmt das Benzin am Wasser auf. Auf welcher Höhe \(h_S\) befindet sich der Schwerpunkt dieses gefüllten Behälters? (Die Masse des Behälters selber wird dabei vernachlässigt.) Die Dichten von Wasser und Benzin sind: \(\rho_{W}=1,0\ \frac{kg}{l}\), \(\rho_{B}=0,75\ \frac{kg}{l}\) Nr. 4446
|
|
|---|---|
| Lösungsweg | |
|
Auf einem homogenen Stab der Länge \(l=5\) liegen 3 Massen, wie in der Graphik angeordnet: \(m_1\) am Ort \(x_1=1\), \(m_3\) am Ort \(x_3=3\) und \(m_4\) am Ort \(x_4=4\). Dabei gilt: \(m_3=m_1\) und \(m_4 = 2\cdot m_1\) Welche Masse muss ein viertes Gewicht am Ort \(x_2=2\) haben, damit der Schwerpunkt genau in der Mitte (in x-Richtung) des Stabes liegt, wenn \(m_1=3\,kg\)? 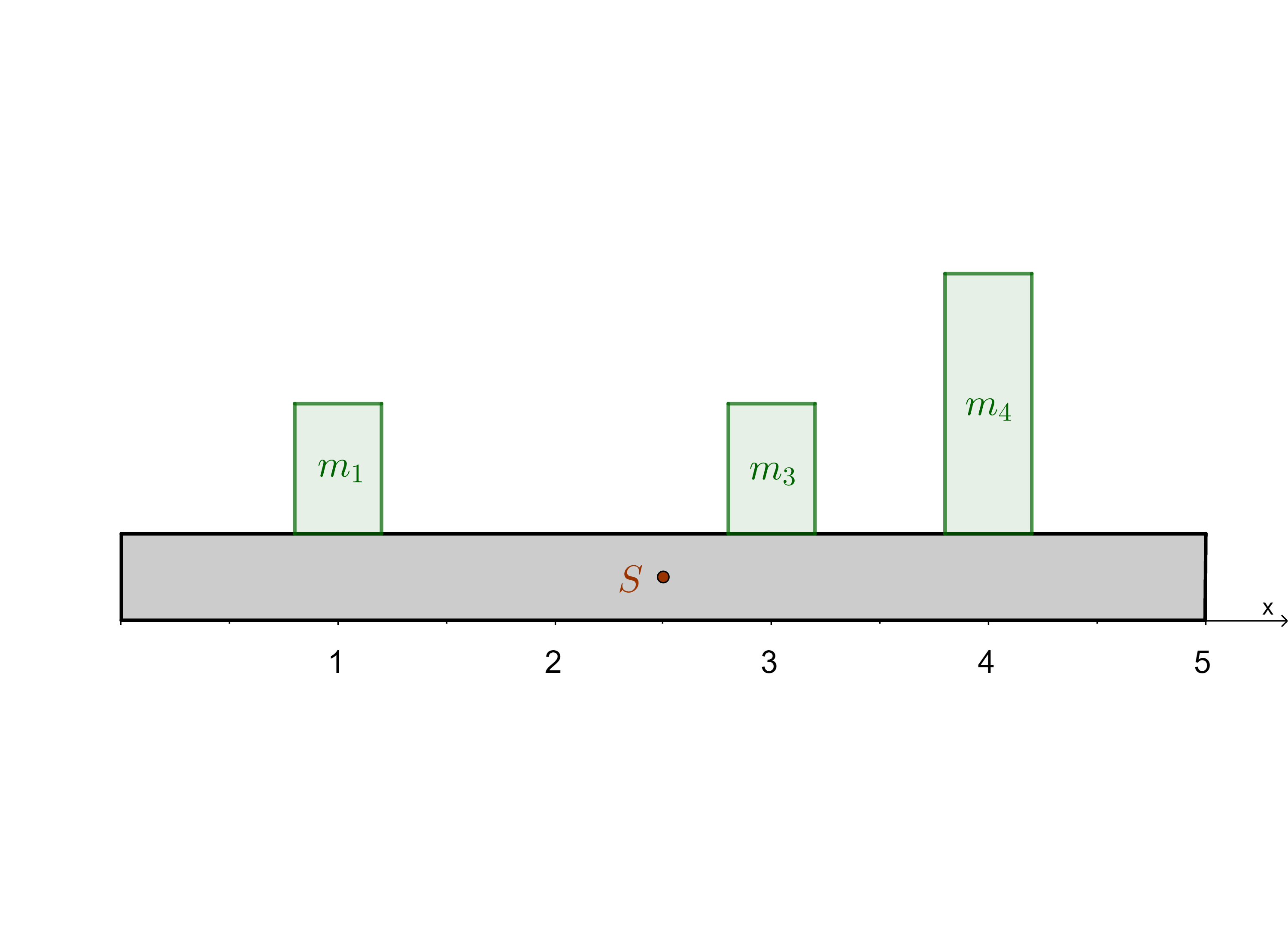 Nr. 4449
|
|
|---|---|
| Lösungsweg | |
|
Welche Aussagen sind korrekt? Ein Kräftepaar besteht aus zwei ... Nr. 4463
|
|
|---|---|
| Lösungsweg | |
|
Ein homogener Balken der Masse \(m_B\) und Länge \(l_B\) wird mit Hilfe eines Gelenks an einer Wand angebracht. Der Balken wird durch ein Seil in horizontaler Position gehalten, das mit ihm einen Winkel \(\theta\) einschließt. An seinem Ende hängt ein Schild der Masse \(m_S\). Weiters sind die Zugkraft des Seils \(\vec F_Z\) sowie die Kraft \(\vec F_P\), die das Gelenk auf den Balken ausübt, eingezeichnet. Wie lauten die Gleichgewichtsbedinungen, sodass sich der Balken im statischen Gleichgewicht befindet? 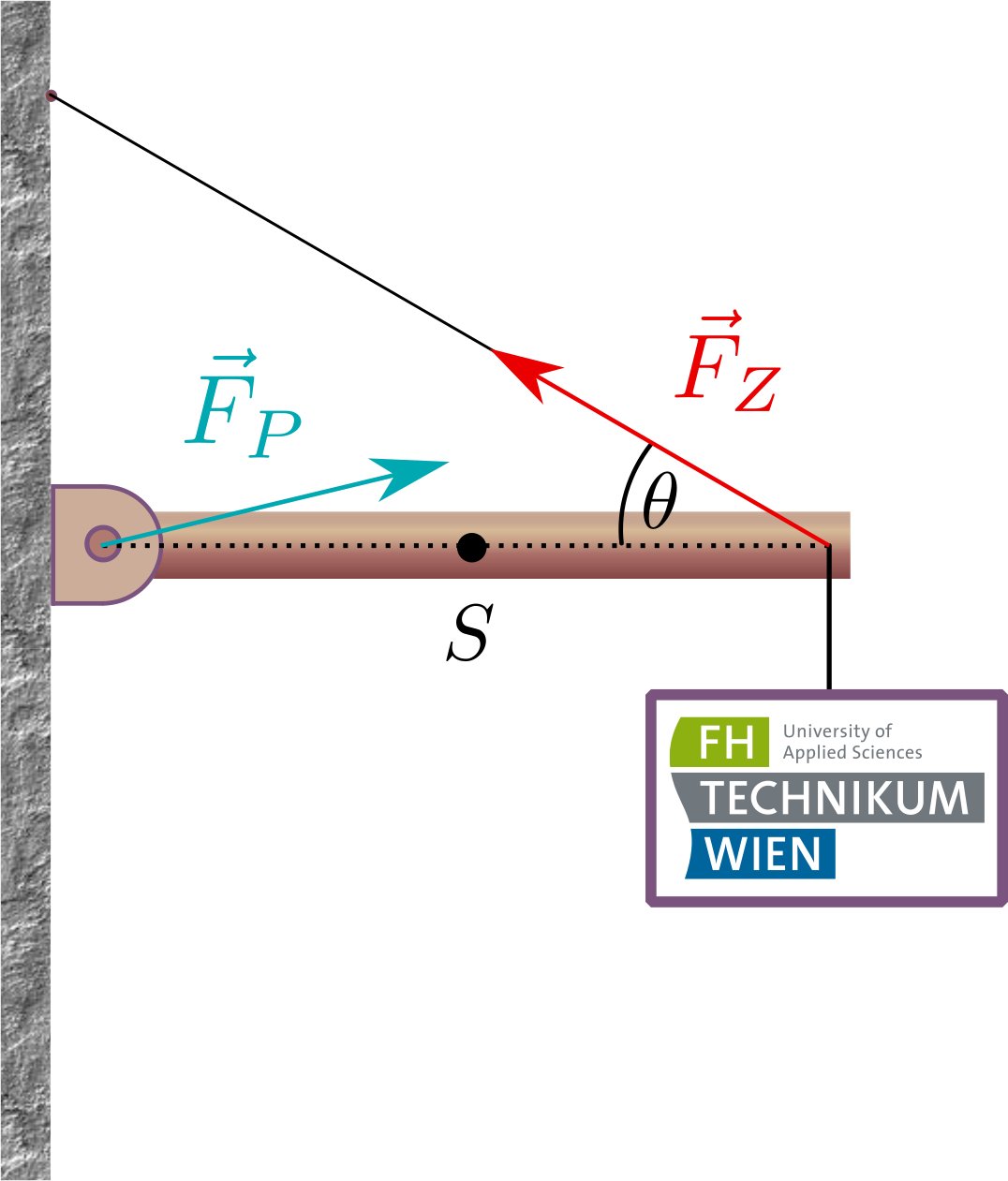 Nr. 4483
|
|
|---|---|
| Lösungsweg | |
|
Zwei Kräfte \(\vec{F_1} \) und \( \vec{F_2}\), die an einem Körper angreifen, befinden sich im Gleichgewicht, wenn ... Nr. 4597
|
|
|---|---|
| Lösungsweg | |
|
Auf einen Balken wirken die drei Kräfte \(\vec F_1\), \(\vec F_2\) und \(\vec F_3\). Wie groß sind die Beträge der Kräfte \(\vec F_2\) und \(\vec F_3\), wenn ein Kräftegleichgewicht vorliegt? Geg.: \(F_1 = 500\,N\), \(\alpha = 50^\circ\), \(\beta= 30^\circ\). 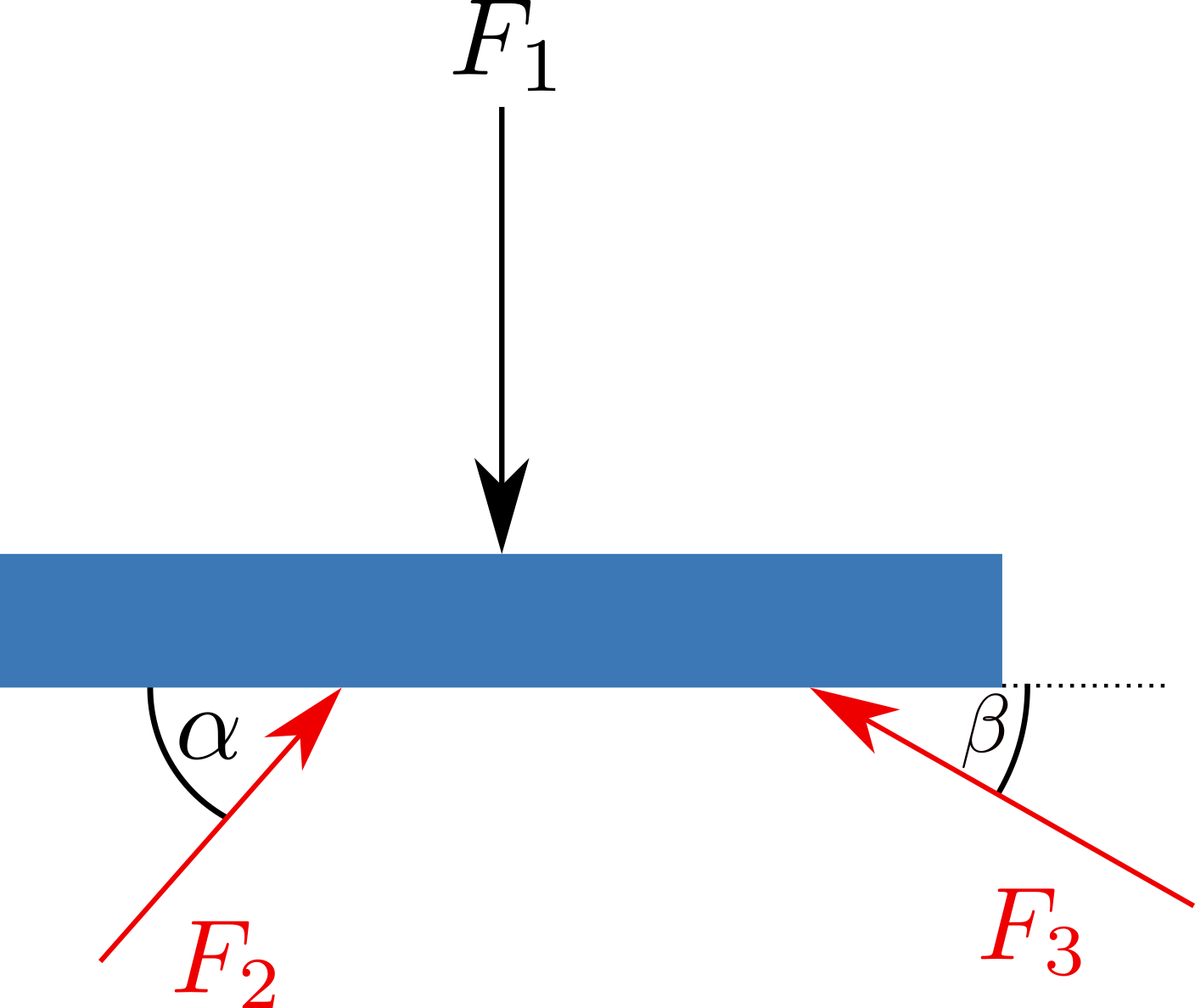 Nr. 4598
|
|
|---|---|
| Lösungsweg | |
|
In einem zentralen Kräftesystem wirken die Kräfte \(F_1 = 160\,N\) und \(F_2 = 220\,N\), die mit der positiven x-Achse die Winkel \(\alpha_1 = 70^\circ\) und \(\alpha_2 = 160^\circ\) einschließen und mit einer Kraft \(F_3\) im Gleichgewicht stehen. Wie groß ist der Betrag der Kraft \(F_3 = |\vec F_3|\)? In welchem Quadranten wirkt diese Kraft? (Tipp: Skizze!) Nr. 4611
|
|
|---|---|
| Lösungsweg | |
|
An einem L-förmigen Bauteil greifen zwei Kräftepaare an. Welchen Betrag müssen die Kräfte \(F_1\) und \(F_2\) haben, sodass das resultierende Moment verschwindet?  Nr. 4612
|
|
|---|---|
| Lösungsweg | |
|
Ein homogener Balken der Länge \(l_0 = 4\,m\) ist in A gelagert und liegt in B auf einer Mauerkante auf. Die Berührung bei A und B sei reibungsfrei. Die Gewichtskraft des Balkens beträgt \(F_G = 800\,N\), die Abmessungen betragen \(l_1 = 2.5\,m\) und \(l_2 = 2\,m\). Berechnen Sie die Beträge der Stützkräfte \(F_A\) und \(F_B\). (Ergebnisse gerundet)  Nr. 4645
|
|
|---|---|
| Lösungsweg | |
|
Ein Balken ist wie abgebildet gelagert. Bestimmen Sie die Reaktionskräfte in den Lagern A und B. Die Masse des Balkens und damit seine Gewichtskraft seien vernachlässigbar. Geg.: \(F = 3.5\,kN\), \(l_1 = 0.8\,m\), \(l_2=2\,m\)  Nr. 4725
|
|
|---|---|
| Lösungsweg | |
|
An einem starren Körper greifen N Kräftepaare (\(N \qquad \geq \qquad 2\)) an. Der Betrag der i-ten einzelnen Kraft wird als \(F_i\) bezeichnet. Wie groß ist die Resultierende \(F_R\) dieses Kraftsystems? Nr. 4756
|
|
|---|---|
| Lösungsweg | |
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!
Bei uns können Sie auch reine Mathematik üben: www.mathe.technikum-wien.at