Fragenliste von Kippmoment
|
Auf einem homogenen Stab der Länge \(l=5\) liegen 3 Massen, wie in der Graphik angeordnet: \(m_1\) am Ort \(x_1=1\), \(m_3\) am Ort \(x_3=3\) und \(m_4\) am Ort \(x_4=4\). Dabei gilt: \(m_3=m_1\) und \(m_4 = 2\cdot m_1\) Welche Masse muss ein viertes Gewicht am Ort \(x_2=2\) haben, damit der Schwerpunkt genau in der Mitte (in x-Richtung) des Stabes liegt, wenn \(m_1=3\,kg\)? 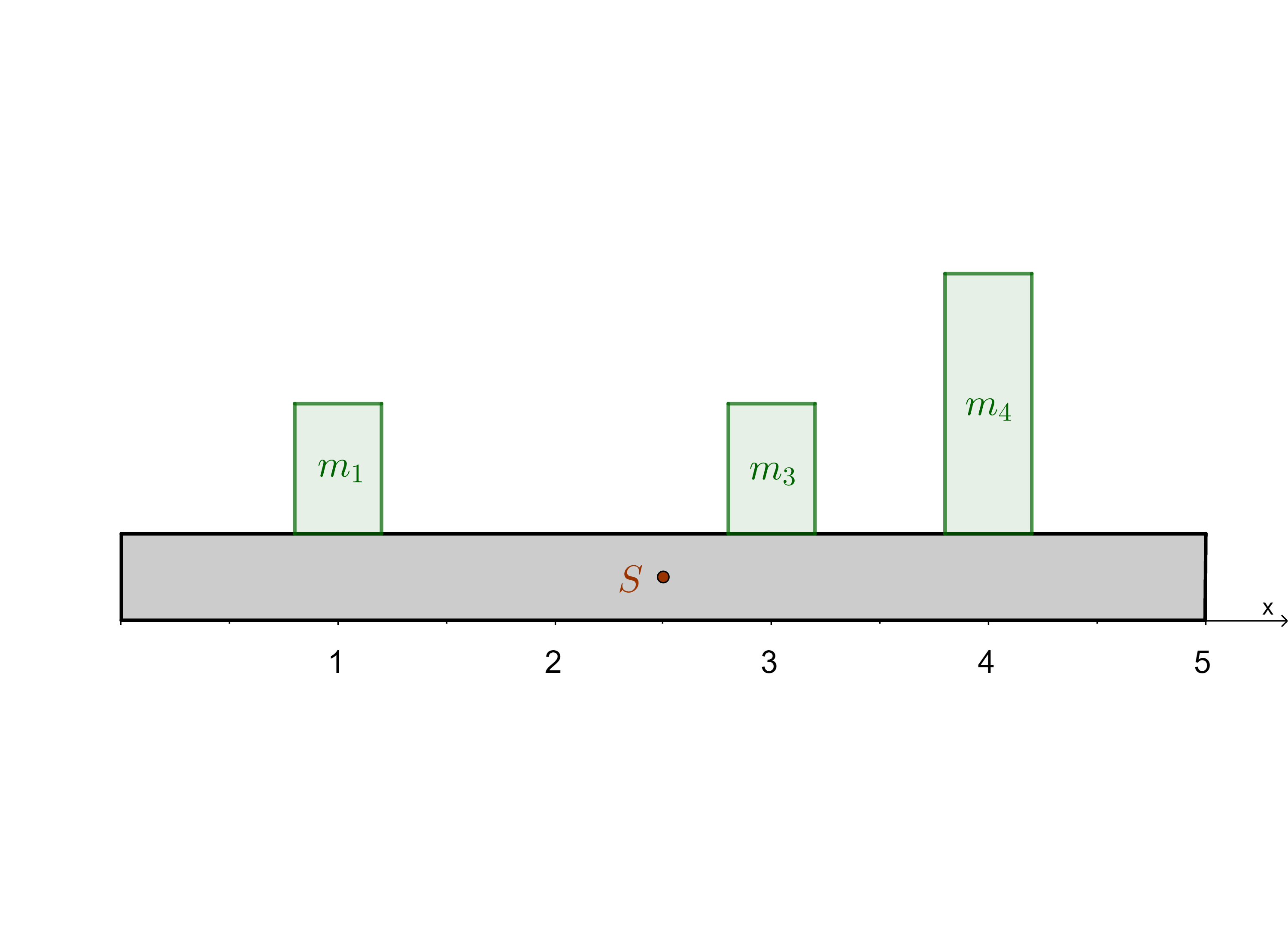 Nr. 4449
|
|
|---|---|
| Lösungsweg | |
|
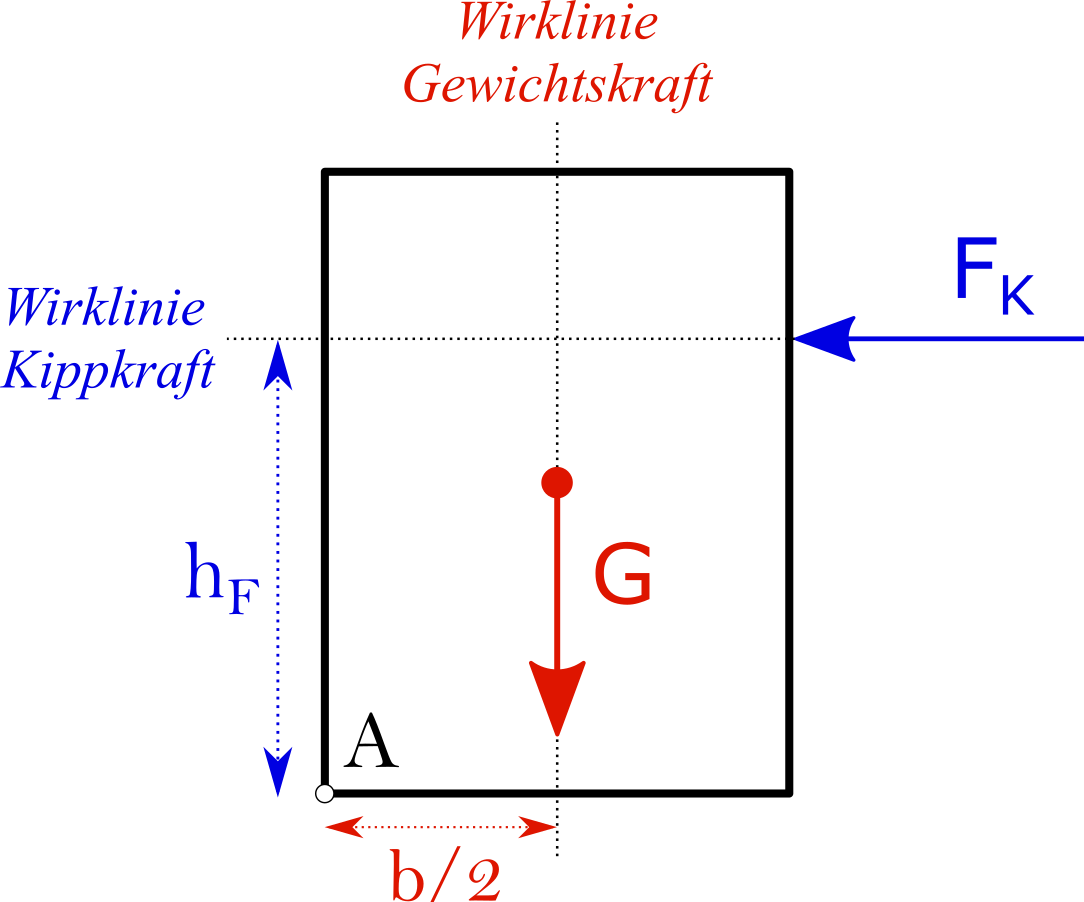
An einem Kasten greifen im Schwerpunkt die Gewichtskraft \(G=1160\, N\) sowie in der Höhe \(h_F\) die Kippkraft \(F_K\) an. Wie groß darf \(F_K\) sein, damit der Kasten gerade nicht umkippt? Gehe dabei von einer (im Mittel) homogenen Verteilung der Masse innerhalb des Kastens aus. Geg.: \(h=175\, cm\), \(h_F= 0,8 \cdot h\), \(b=105\, cm\) 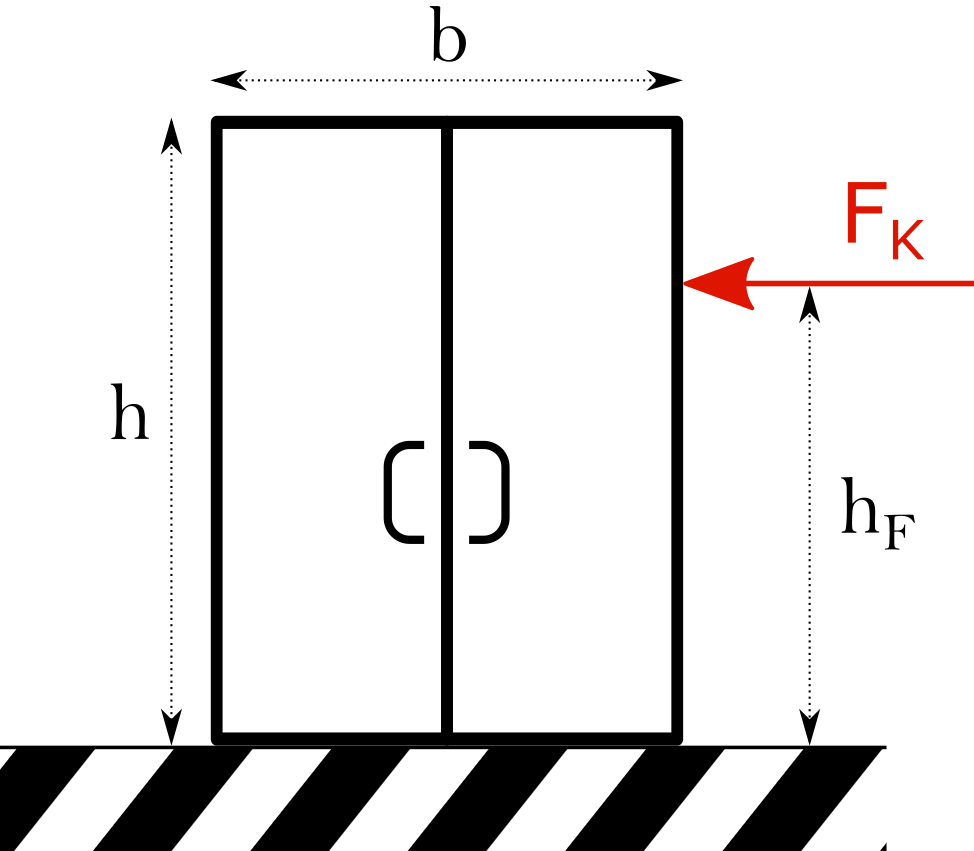 Nr. 4476
|
|
|---|---|
| Lösungsweg | |
|
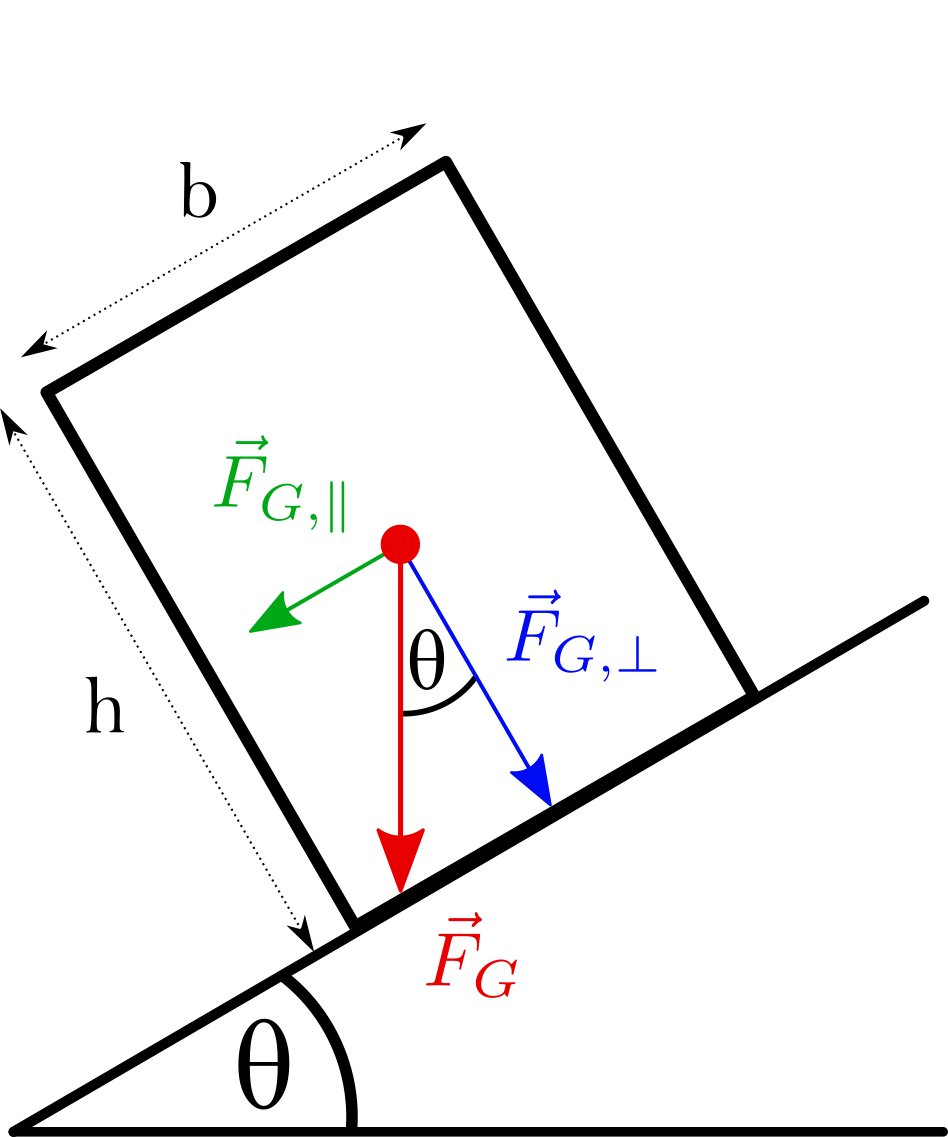
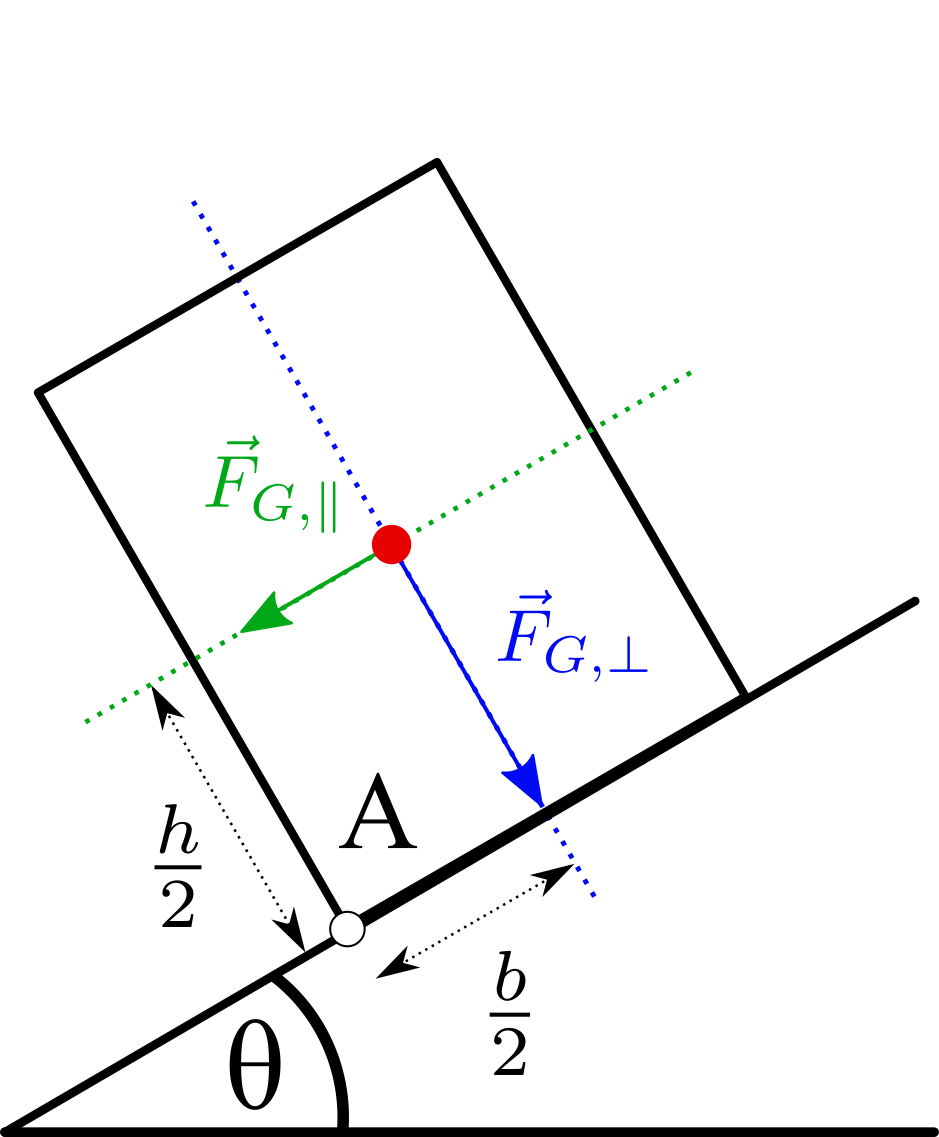
Ein Kasten der Höhe \(h = 184\,cm\) und Breite \(b = 115\, cm\) steht auf einer schiefen Ebene mit dem Neigungswinkel \(\theta\). Die Gewichtskraft \(F_G\) des Kastens greift im Schwerpunkt an, der sich in dessen Mittelpunkt befindet Berechnen Sie den maximalen Neigungswinkel \(\theta_{\mathrm{max}}\), sodass der Kasten nicht kippt. 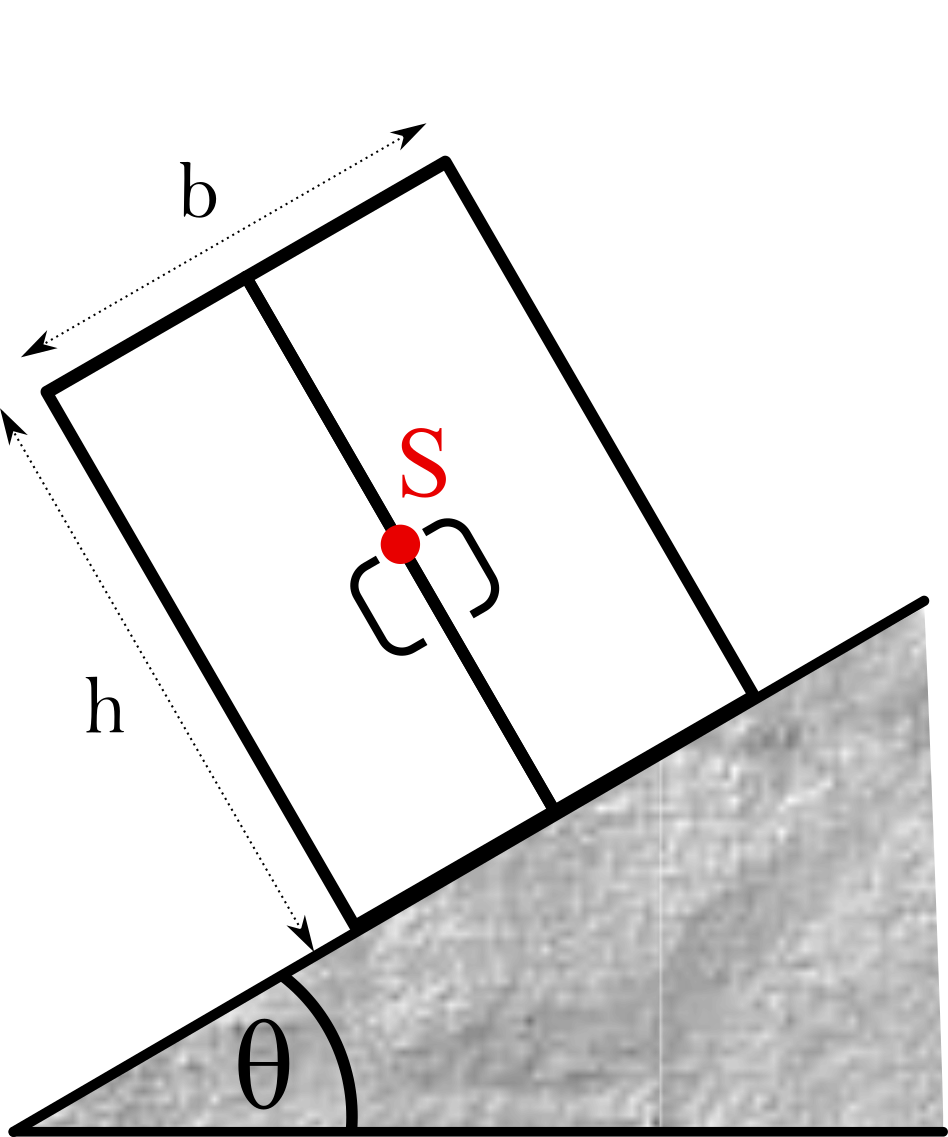 Nr. 4478
|
|
|---|---|
| Lösungsweg | |
|
Ist es möglich, einen würfelförmigen Körper mit Kantenlänge \(l_0\) auf einer ebenen Fläche durch eine waagrecht wirkende Kraft \(F_K\) zum Kippen zu bringen, wenn der Angriffspunkt dieser Kraft auf den Würfel unterhalb des Schwerpunkts liegt? Die auf den Körper wirkende Gewichtskraft \(F_G\) greift im Schwerpunkt auf der Höhe \(y_{F_G} = \frac{l_0}{2}\) an. Der Kippunkt ist in der Abbildung mit A bezeichnet, der Angriffspunkt der Kraft \(F_K\) liegt auf der Würfelkante, wobei \(0 \qquad < \qquad y_{F_K} \qquad < \qquad \frac{l_0}{2}\) gilt. Gehen Sie davon aus, dass die Haftreibung zwischen der Fläche und dem Würfel groß genug sei, sodass der Körper nicht rutscht. Begründen Sie Ihre Antwort! 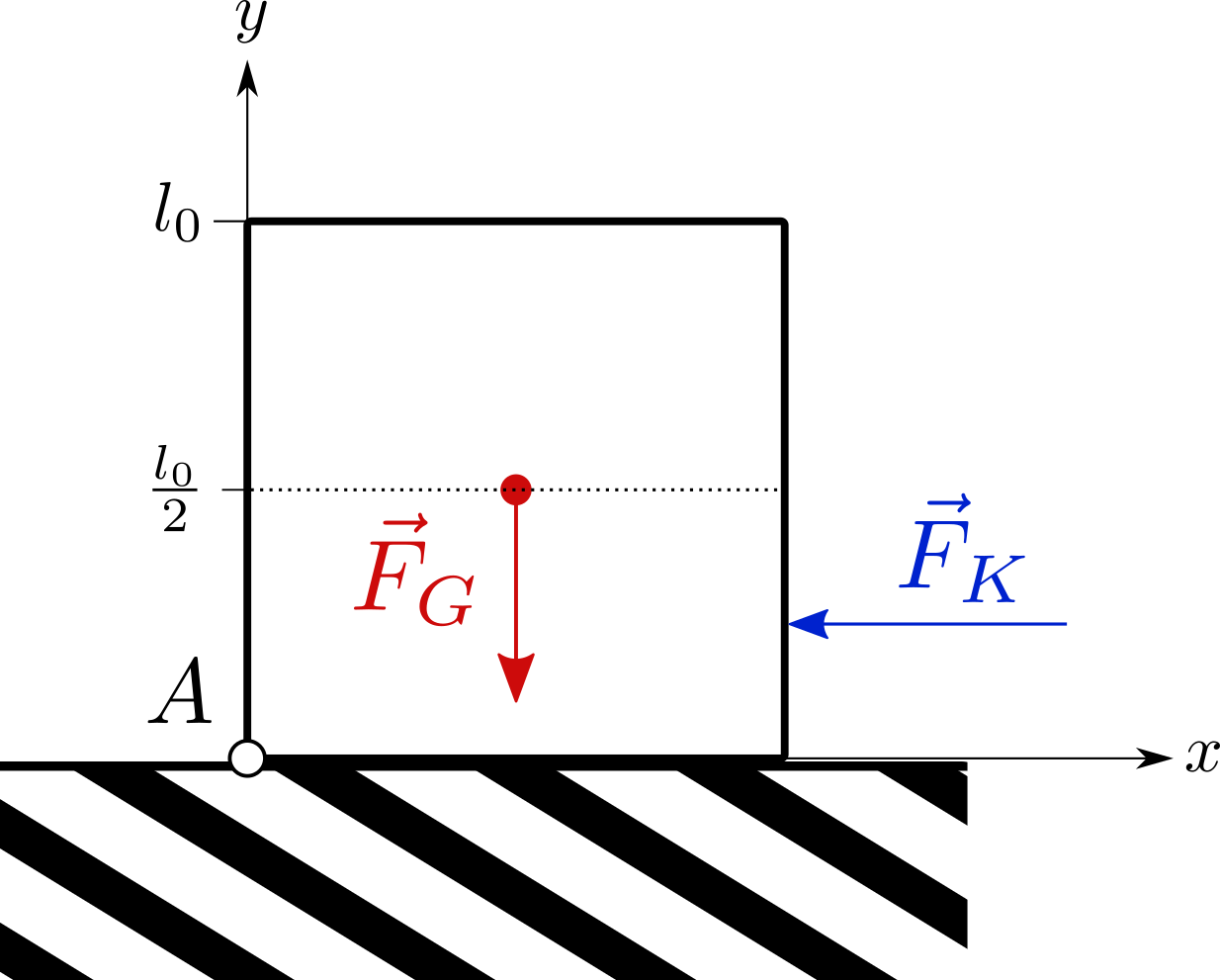 Nr. 4479
|
|
|---|---|
| Lösungsweg | |
|
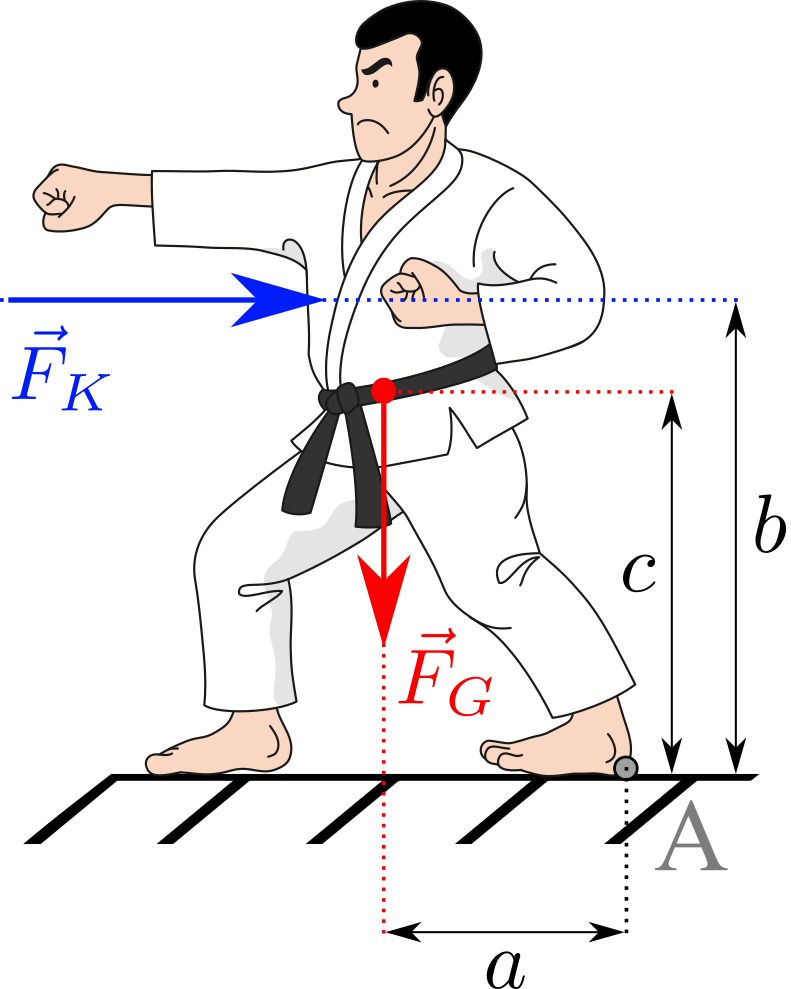
Ein Karatekämpfer mit Eigengewicht \(F_G = 900\,N\) wird von seinem Gegner mit der Kraft \(F_K\) gegen den Brustkorb gedrückt. Bei welcher Kraft \(F_K\) verliert der Karatekämpfer sein Gleichgewicht und kippt rückwärts um? Dabei gilt: \(c = \frac{3}{2}\cdot a\) und \(c = \frac{3}{4} \,b\). 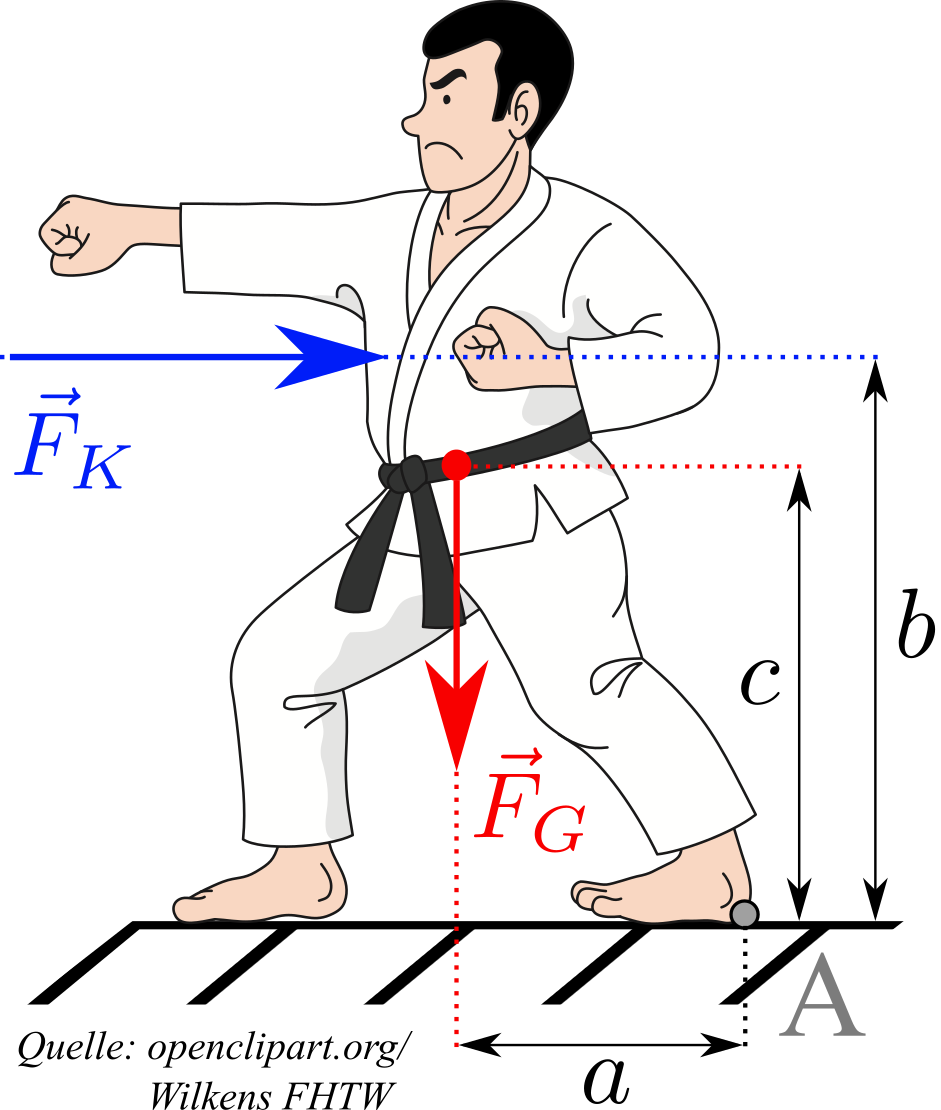 Nr. 4540
|
|
|---|---|
| Lösungsweg | |
|
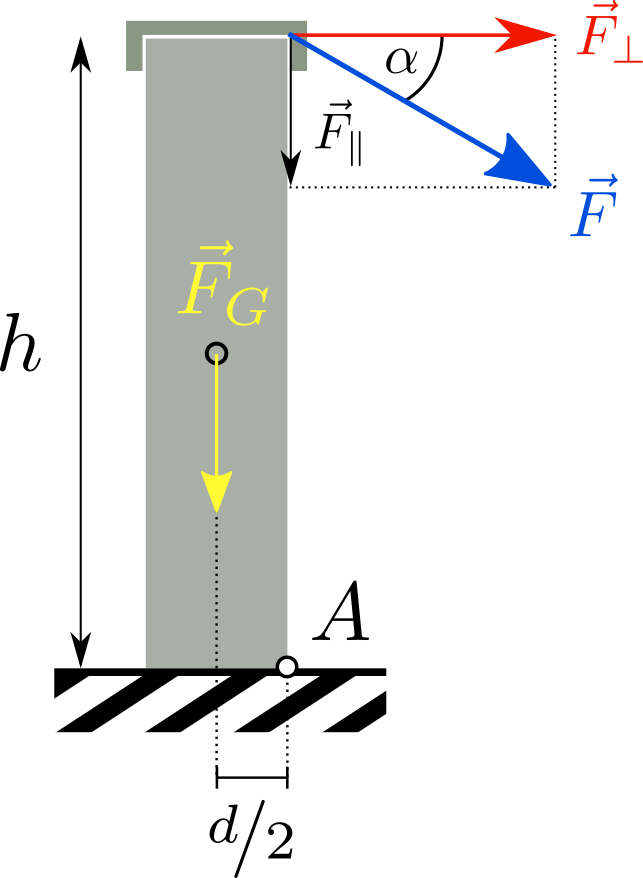
Ein Mauerstück mit \(F_G = 18\,kN\) Gewichtskraft soll mit Hilfe eines Seils umgekippt werden, das unter einem Winkel \(\alpha = 25^\circ\) an der Mauerkrone zieht. Die Höhe der Mauer beträgt \(h=2,2\,m\) und ihre Dicke \(d= 40 \,cm\). Berechnen Sie die zum Ankippen erforderliche Seilkraft \(F = |\vec F|\). 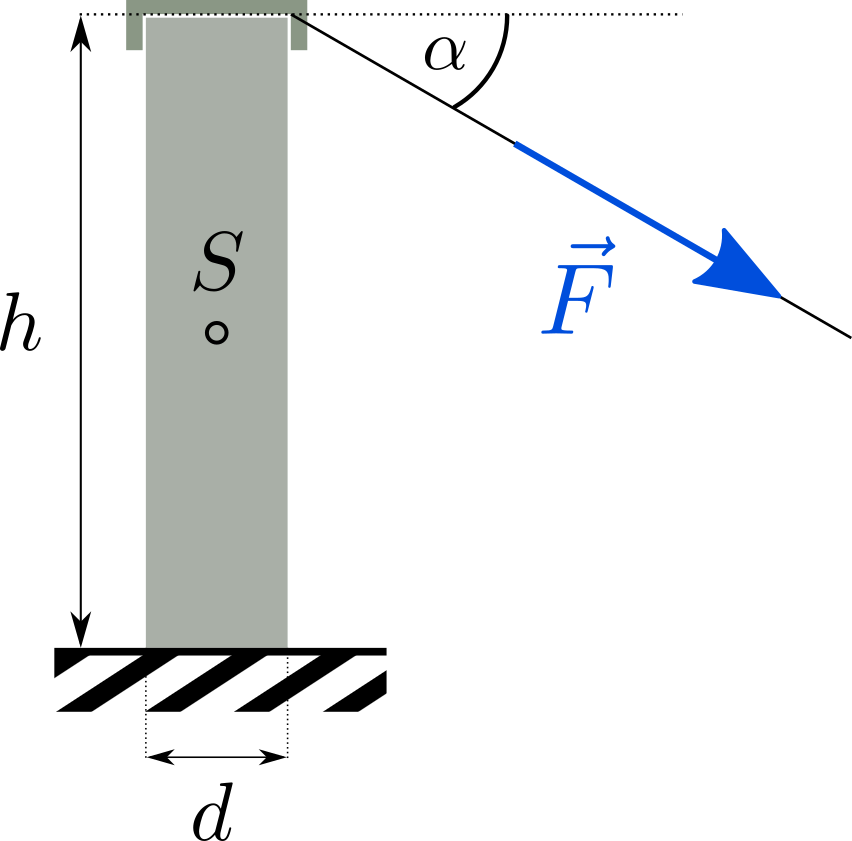 Nr. 4564
|
|
|---|---|
| Lösungsweg | |
|
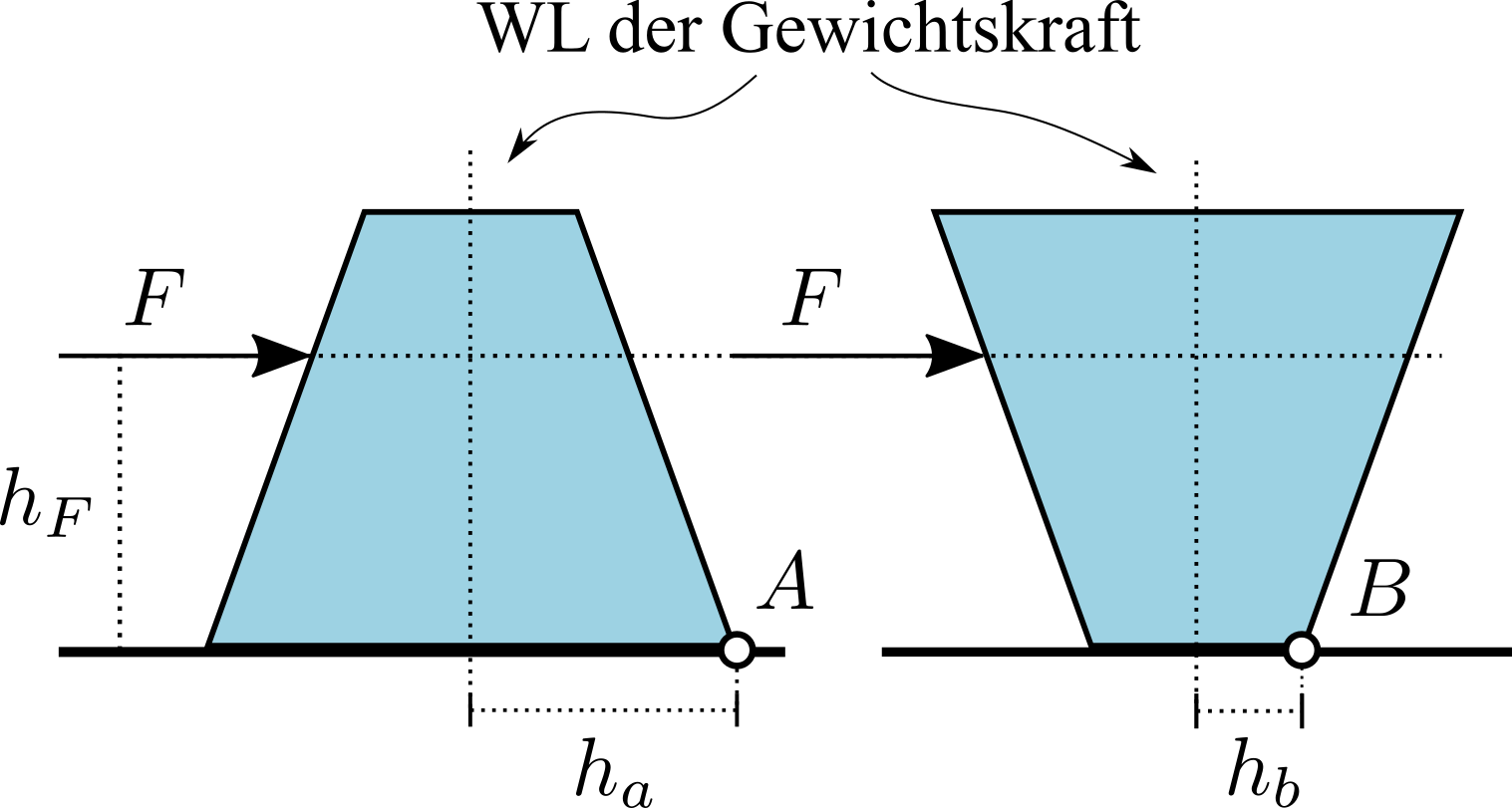
Ein homogener Körper mit trapezförmigem Querschnitt wird durch eine waagrecht wirkende Kraft \(F\) belastet, die in der Höhe \(h_F\) angreift. In welcher Stellung des Körpers ist die Standsicherheit S größer, wenn er auf der langen (a) oder auf der kurzen Seite (b) aufliegt? Die Höhe \(h_F\) bleibt dabei in beiden Fällen gleich. Achten Sie auf eine korrekte Begründung! 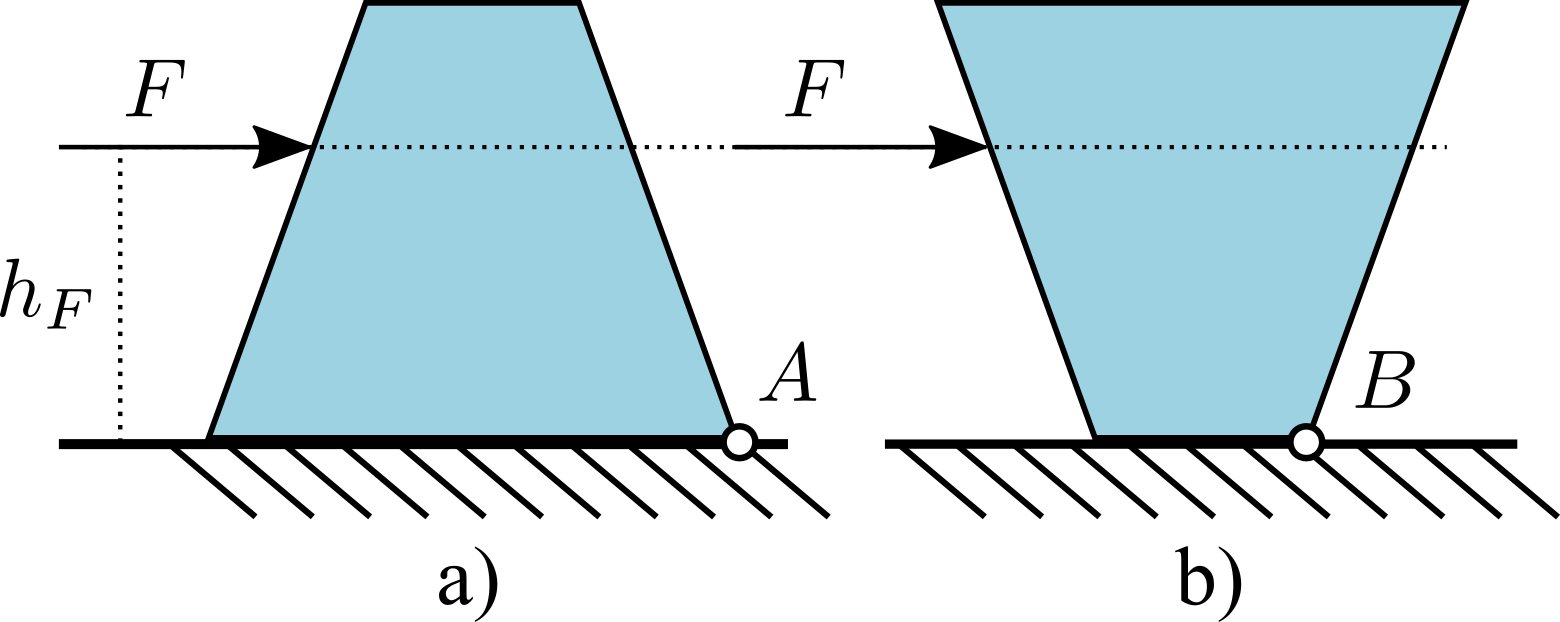 Nr. 4731
|
|
|---|---|
| Lösungsweg | |
|
Wie nahe am Rand des abgebildeten Tisches mit einer Masse von \(30\,kg\) kann eine Person mit Masse \(75\,kg\) sitzen, ohne dass der Tisch umkippt? 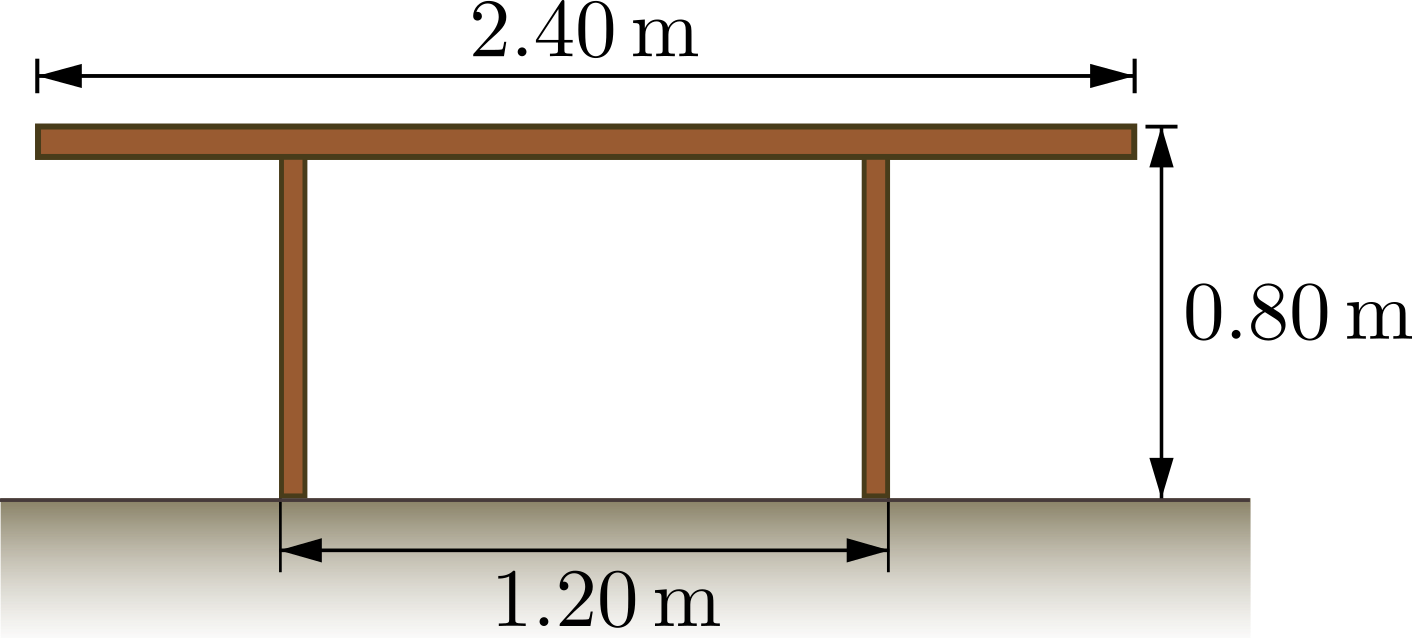 Nr. 4732
|
|
|---|---|
| Lösungsweg | |
|
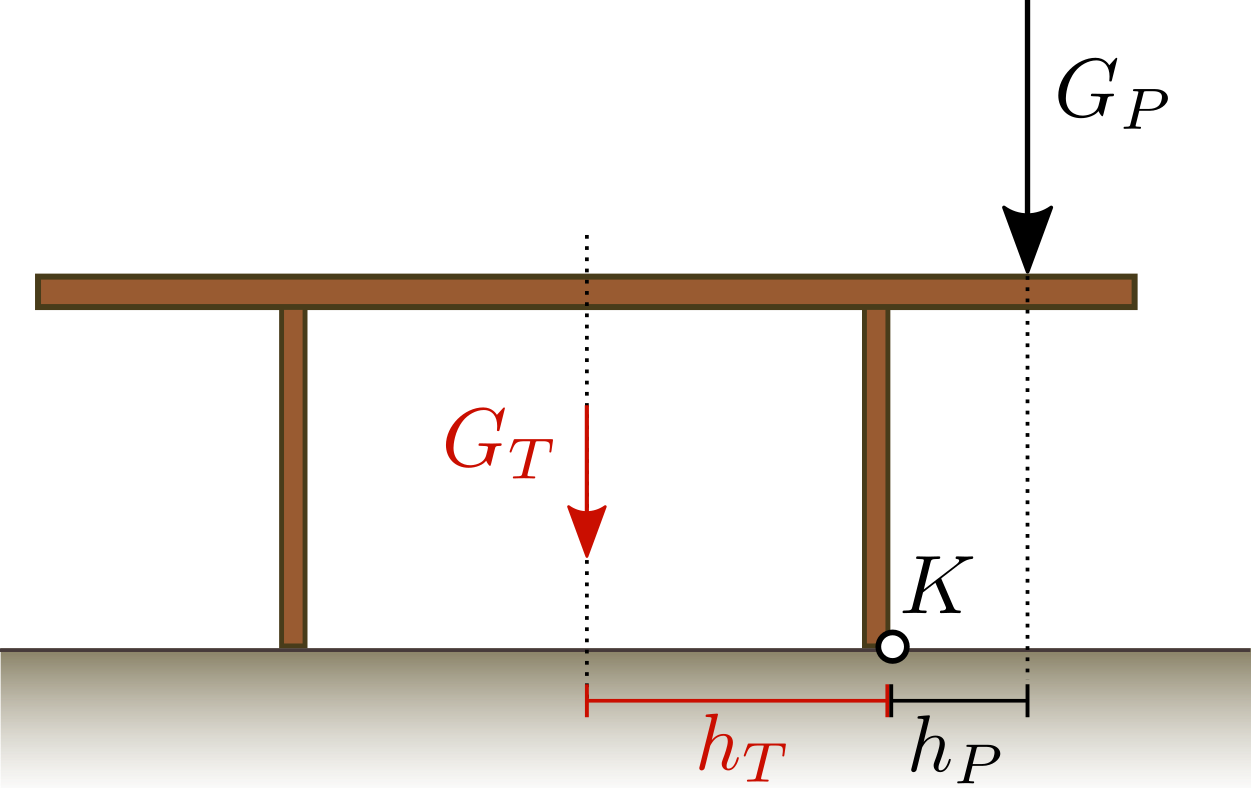
Eine Person mit Masse \(m_P = 80\,kg\) sitzt so an einem Tisch, dass ihre Gewichtskraft im Abstand \(l_P = 20\,cm\) vom Rand des Tisches angreift. Der Tisch kippt dabei nicht um. Welche Masse \(m_T\) muss der Tisch mindestens haben? 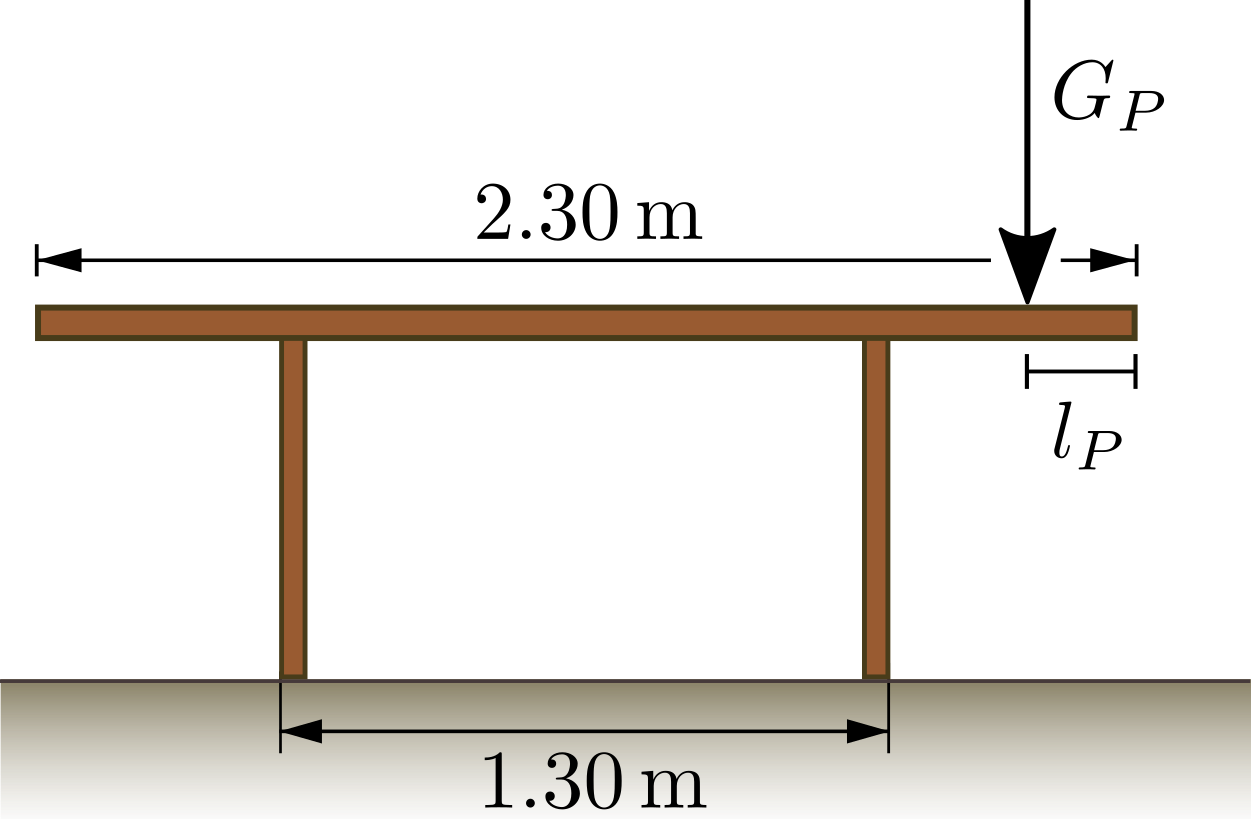 Nr. 4757
|
|
|---|---|
| Lösungsweg | |
NEWS
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!