Lösungsweg
-
Antwort 1 ist korrekt.
Zur Lösung dieser Aufgabe ist ein gutes Verständnis der Kirchhoffschen Regeln notwendig.
Mit Hilfe dieser Gesetze können die 4 Ohmschen Widerstände \(R_1\), \(R_2\), \(R_3\), \(R_4\) aus Schaltbild (1) zu einem Widerstand \(R\) zusammengefasst werden.
Um zu überprüfen ob die Berechnung des Ohmschen Widerstands \(R\) korrekt verlaufen ist, kann der Gesamtstrom \(I\) in beiden Schaltbildern bestimmt werden. Für eine korrekte Berechnung muss Der Gesamtstrom \(I\) in beiden Schaltbildern gleich sein.
-
Die Aufgabe erfolgt in Teilschritten.
Im ersten Schritt werden die Widerstände \(R_3\) und \(R_4\) zu einem Widerstand \(R_{34}\) zusammengefasst.
Eine Serienschaltung von mehreren Ohmschen Widerständen durch welche der gleiche elektrische Strom fließt können durch dessen Summe ersetzt werden. Dies folgt aus der Maschenregel.
(Vorsicht: Dies geht wirklich nur wenn der gleiche Strom durch die Widerstände fließt. Wir können also NICHT! die drei Widerstände \(R_1\), \(R_3\) und \(R_4\) durch dessen Summe ersetzen. Durch \(R_1\) fließt der Gesamtstrom \(I\) und durch die Widerstände \(R_3\) und \(R_4\) fließt der Teilstrom \(I_2\).)
Wir ersetzen die Widerstände \(R_3\) und \(R_4\) durch dessen Summe \(R_{34}\).
\(R_{34} \,\, = \,\, R_3 \,\, + \,\, R_4 \,\, = \,\, 30 \, \Omega \,\, + \,\, 60 \,\, \Omega \,\, = \,\, 90 \,\, \Omega\)
-

Die nebenstehende Skizze beschreibt nun das neue Schaltbild:
Im nächsten Schritt wird die Parallelschaltung der beiden Widerstände \(R_2\) und \(R_{34}\) in einen Widerstand \(R_{234}\) zusammengefasst.
Eine Parallelschaltung von mehreren Widerständen welche die gleiche Quellspannung besitzen wird durch die Summe von dessen Kehrwerten ersetzt.
Anwendung der Knotenregel auf das Schaltbild liefert die Gleichung: \(I \,\, = \,\, I_1 \,\, + \,\, I_2 \,\,\). Anschließende Anwendung des Ohmschen Gesetzes liefert die Gleichung: \(I \,\, = \,\, \frac{U_0}{R_2} \,\, + \,\, \frac{U_0}{R_{34}} \,\, \,\, = \,\, U_0 \,\, \cdot \,\, (\,\, \frac{1}{R_2} \,\, + \,\, \frac{1}{R_{34}} \,\, ) \)
Damit können die Kehrwerte der beiden Widerstände \(R_2\) und \(R_{34}\) durch den Kehrwert des neuen Widerstands \(R_{234}\) ersetzt werden : \(\frac{1}{R_{234}} \,\, = \,\, \frac{1}{R_2} \,\, + \,\, \frac{1}{R_{34}} \,\,\)
Bei Addition und Subtraktion von Brüchen muss ein gemeinsamer Nenner gebildert werden. Anschließende Umstellung der Gleichung liefert uns den Ausdruck:
\(R_{234} \,\, = \,\, \frac{\,\, R_{2} \,\, \cdot \,\, R_{34} \,\,}{\,\, R_{2} \,\, + \,\, R_{34} \,\,} \,\, \)
\(R_{234} \,\, = \,\, \frac{\,\, 45 \, \Omega \,\, \cdot \,\, 90 \, \Omega \,\,}{\,\, 45 \, \Omega \,\, + \,\, 90 \, \Omega \,\,} \,\, = \,\, 30\, \Omega\)
-
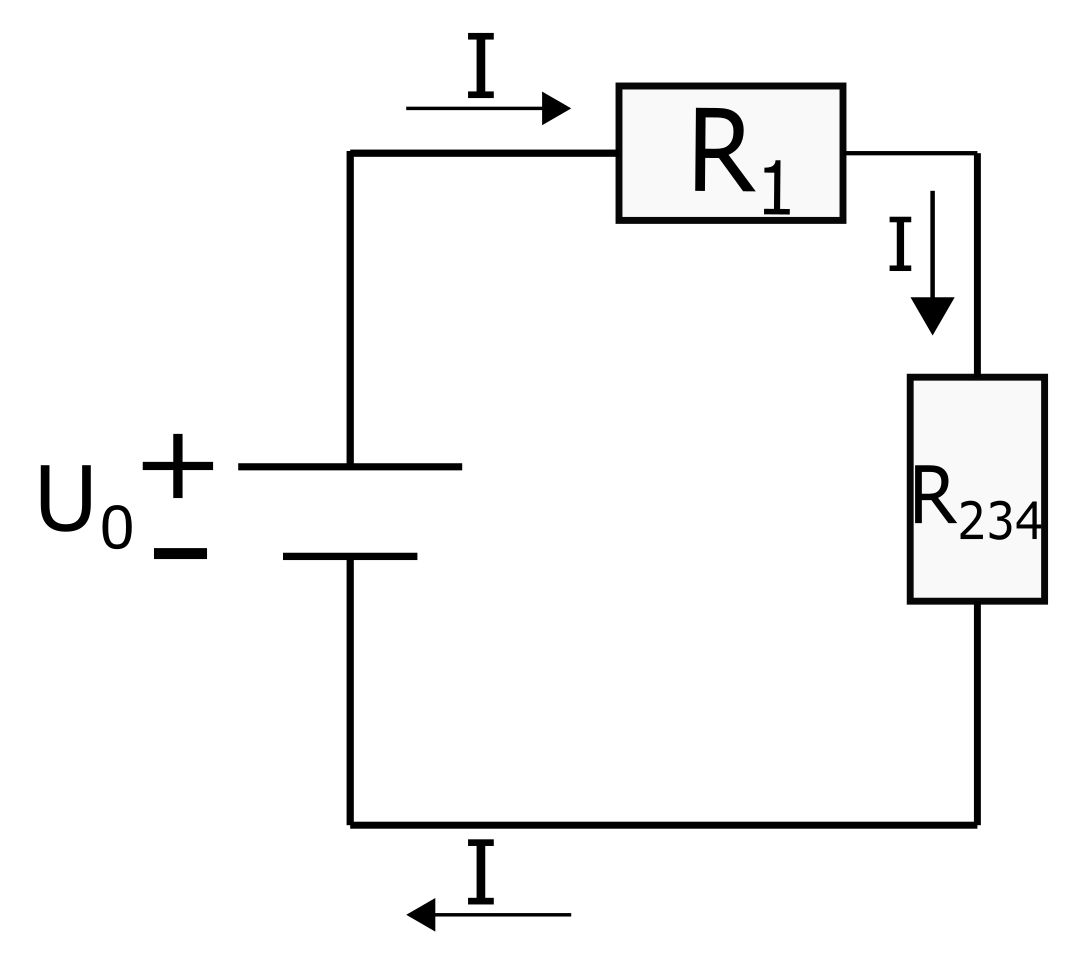
Die nebenstehende Skizze beschreibt das neue Schaltbild:
Durch die beiden Widerstände \(R_{234}\) und \(R_1\) fließ jetzt der selbe Gesamtstrom \(I\) und daher können die beiden Widerstände (wie im ersten Schritt) durch dessen Summe ersetzt werden.
\(R \,\, = \,\, R_1 \,\, + \,\, R_{234} \,\, = \,\, 10 \, \Omega \,\, + \,\, 30 \, \Omega \,\, = \,\, 40 \, \Omega \,\, \)
Jetzt ist unser Schaltbild gleich dem vereinfachten Schaltbild (2).
Jetzt muss nur noch der Strom \(I\) selbst berechnet werden.
Dies geschieht am Einfachsten durch Anwendung des Ohmschen Gesetzes auf das Ersatzschaltbild (2).
\(I \,\, = \,\, \frac{U_0}{R} \,\, = \,\, \frac{8 \,\, V}{40 \,\, \Omega} \,\, = \,\, 0.2 \,\, A \,\, \)
Wenn man überprüfen möchte ob man den Widerstand \(R\) richtig bestimmt hat, dann berechnet man auch den \(I\) den Gesamtstrom im Schaltbild (1).
Dazu müssen erst die beiden Teilströme \(I_1\) und \(I_2\) bestimmt werden. Dies erfordert aber in diesem Beispiel das Lösen eines Gleichungssystems mit 3 Unbekannten \(I_1\), \(I_2\) und \(I\) worauf hier aber nicht weiter eingegangen wird.
|





