Lösungsweg
-
Antwort 3 und 4 sind korrekt.
Der Carnot'sche Kreisprozess stellt das Arbeitsprinzip einer ideal wirkenden Wärmekraftmaschine dar. Wärmekraftmaschinen haben die Aufgabe, Wärme, welche aus einem Wärmespeicher geholt wird, in mechanische Arbeit umzuwandeln. Mit "ideal wirkend" meint man, dass Reibung und jegliche Wärmeverluste ignoriert werden und jede Zustandsänderung des Kreisprozesses reversibel ist.
Der Carnot'sche Kreisprozess besteht aus 4 Takten. 2 isotherme und 2 adiabatische Zustandsänderungen. Um die gesamte Arbeit \(W\)in einem Zyklus zu bestimmen, müssen die einzelnen Zustandsänderungen genauer betrachtet werden.
-
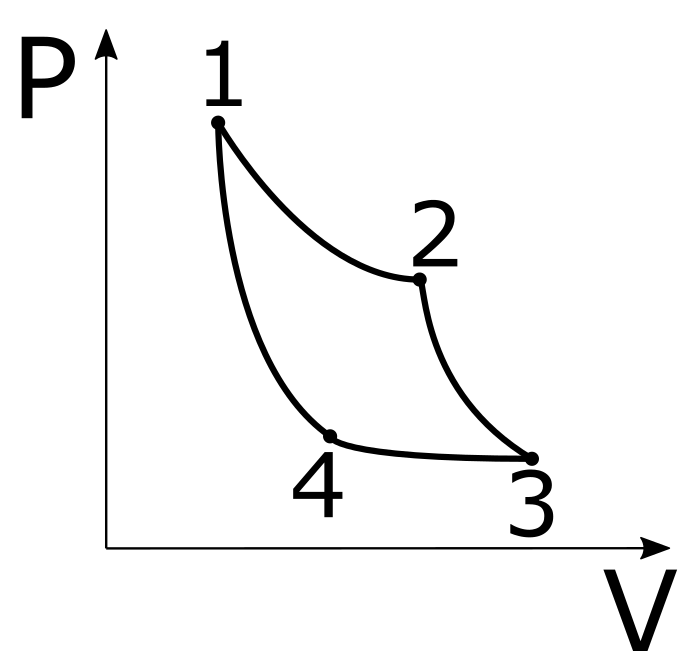
Die nebenstehende Graphik stellt den Carnot'schen Kreisprozess in einem P-V-Phasendiagramm dar.
Das betrachtete System ist wie üblich das ideale Gas, welches sich in einem Zylinder mit frei beweglichem Kolben befindet.
Die Basis für jede Zustandsänderung ist der 1. Hauptsatz der Thermodynamik: \(dU \,\, = \,\, dQ \,\, + \,\, dW\)
-
Das System startet beim Zustand \(1\) (mit gewissem Druck \(p_{1}\) , Volumen \(V_{1}\) und Temperatur \(T_{1}\)).
Der erste Takt des Carnot-Kreisprozesses beschreibt die isotherme Zustandsänderung des Gases (von Zustand \(1\) bist \(2\) im P-V-Diagramm).
Bei einer isothermen Zustandsänderung bleibt die Temperatur \(T\) des Gases konstant. Da aber die innere Energie \(U\) des Gases eine Funktion von dessen Temperatur ist, gilt für die Änderung der inneren Energie: \(dU \,\, = \,\, 0\). Daher reduziert sich der 1. Hauptsatz zu \(- \,\, dW \,\, = \,\, dQ \,\,\). Das Gas expandiert isotherm. Die für diese Expansion benötigte Arbeit \(W_{1 \,\, 2}\) wird aus dem Wärmespeicher als Wärme \(Q_{1 \,\, 2}\) entnommen.
Die Gleichung \(- \,\, dW \,\, = \,\, dQ \,\,\) wird auf beiden Seiten integriert. (Für die Volumsänderungsarbeit gilt: \(dW \,\, = \,\, p \,\, \cdot \,\, dV\)und man integriert vom Anfangsvolumen \(V_{1}\) zum Endvolumen \(V_{2}\). In den Druck \(p\) wird der Ausdruck \(\frac{n \,\, \cdot \,\, R \,\, \cdot \,\, T}{V}\) eingesetz welcher aus der idealen Gasgleichung kommt.)
\(- \,\, W_{1 \,\, 2} \,\, = \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, T_{1} \,\, \cdot \,\, ln \left( \frac{V_{2}}{V_{1}} \right)\)
Hierbei steht das negative Vorzeichen dafür, dass die Arbeit nicht ins System reingesteckt wird, sondern das System diese Arbeit ausführt und praktisch an die Umgebung abgibt. Das Gas befindet sich jetzt im Zustand \(2\) (mit gewissem Druck \(p_{2}\), Volumen \(V_{2}\) und gleichbleibender Temperatur \(T_{1}\)).
In der 2. Zustandsänderung (vom Zustand \(2\) bis \(3\)) wird das Gas adiabatisch expandiert. Keine Wärme wird mit der Umgebung ausgetauscht. Der erste Hauptsatz reduziert sich auf die Form: \(dU \,\, = \,\, - \,\, dW\). Hier wieder das negative Vorzeichen weil, das System die Arbeit selbst ausführt. Dadurch reduziert sich die innere Energie des Gases und dessen Temperatur muss sinken.
Der Wärmefluss \(dQ\) kann durch die Masse \(m\) und die Wärmekapazität \(c\) dargestellt werden: \(dQ \,\, = \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, dT\) Da aber die mechanische Arbeit nur eine andere Form der Energie ist, kann diese ebenso dargestellt werden: \(- \,\ dW \,\, = \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, dT\)
Wenn jetzt auf beiden Seiten integriert wird, dann erhält man: \(- \,\, W_{2 \,\, 3} \,\, = \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, (T_{2} \,\, - \,\, T_{1})\)
Nach Ausführung dieser adiabatischen Expansionsarbeit, befindet sich das Gas im Zustand \(3\) (mit gewissem Druck \(p_{3}\), Volumen \(V_{3}\) und Temperatur \(T_{2}\)).
Nun folgt eine weitere isotherme Zustandsänderung (von Zustand \(3\) bis Zustand \(4\) im P-V-Phasendiagramm). Diesmal wird das Gas aber komprimiert. Das bedeutet, mechanische Arbeit wird in das System hineingesteckt und um diese zu kompensieren (die innere Energie darf sich beim isothermen Prozess nicht ändern), wird Wärme aus dem Gas herausfließen und dem Wärmespeicher zugeführt. Es gilt jetzt für den 1. Hauptsatz: \(\,\, dW \,\, = \,\, - \,\, dQ \,\,\) Diesmal wird Arbeit in das System hineingesteckt und daher erhält die Änderung der Arbeit ein positives Vorzeichen. Wärme wird hingegen aus dem System rausfließen und daher erhält der Wärmeterm ein negatives Vorzeichen.
Die selbe Integration wird wie beim 1. Takt ausgeführt. Für die Kompressionsarbeit gilt:
\(\,\, W_{3 \,\, 4} \,\, = \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, T_{2} \,\, \cdot \,\, ln \left( \frac{V_{4}}{V_{3}} \right)\)
Nach Ausführung dieser isothermen Kompressionsarbeit, befindet sich das Gas im Zustand \(4\) (mit gewissem Druck \(p_{4}\), Volumen \(V_{4}\) und Temperatur \(T_{2}\)).
Die letzte Zustandsänderung (von Zustand \(4\) zurück zum Zustand \(1\)) ist wieder adiabatisch. Das Gas wird weiter komprimiert, bis es sich wieder im Ausgangangszustand \(1\) befindet (besitzt danach wieder den Druck \(p_{1}\) und Volumen \(V_{1}\)). Es wird wieder genauso integriert wird im 2. Takt:
\(\,\, W_{4 \,\, 1} \,\, = \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, (T_{1} \,\, - \,\, T_{2})\)
Nach Ausführung dieser adiabatischen Kompressionsarbeit befindet sich das Gas wieder im Zustand \(1\) (mit gewissem Druck \(p_{1}\), Volumen \(V_{1}\) und Temperatur \(T_{1}\)).
Es wurden jetzt alle Teilbeiträge zur Arbeit berechnet. Im nächsten Schritt werden diese zur Gesamtarbeit summiert.
-
Die gesamte Arbeit \(W\) ist die Summe aller Arbeitsbeiträge, wobei auf die korrekten Vorzeichen geachtet werden muss. Arbeitsbeiträge, welche ins System hineingeführt werden (Kompressionen bei Takt 3 und 4) erhalten ein positives Vorzeichen, Arbeitsbeiträge welche das System ausführt (Expansionen bei Takt 1 und 2) erhalten ein negatives Vorzeichen.
\(W \,\, = \,\, - \,\, W_{1 \,\, 2} \,\, + \,\, (- \,\, W_{2 \,\, 3} \,\,) \,\, + \,\, W_{3 \,\, 4} \,\, + \,\, W_{4 \,\, 1}\)
\(W \,\, = \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, T_{1} \,\, \cdot \,\, ln \left( \frac{V_{2}}{V_{1}} \right) \,\, + \,\, \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, (T_{2} \,\, - \,\, T_{1}) \)
\(+ \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, T_{2} \,\, \cdot \,\, ln \left( \frac{V_{4}}{V_{3}} \right) \,\, + \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, (T_{1} \,\, - \,\, T_{2})\)
Beim letzten Teilbeitrag \(\,\, c \,\, \cdot \,\, m \,\, \cdot \,\, (T_{1} \,\, - \,\, T_{2})\) kann das negative Vorzeichen herausgehoben werden und damit ändert sich der Beitrag zu \(- \,\, c \,\, \cdot \,\, m \,\, \cdot \,\, (T_{2} \,\, - \,\, T_{1})\). Dann kürzen sich aber dieser und der 2. Teilbeitrag - die beiden adiabatischen Arbeitsbeiträge heben sich gegenseitig auf.
Es gilt daher für die Arbeit \(W\):
\(n \,\, \cdot \,\, R \,\, \cdot \,\, T_{1} \,\, \cdot ln \left( \frac{V_{2}}{V_{1}} \right) \,\, + \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, T_{2} \,\, \cdot ln \left( \frac{V_{4}}{V_{3}} \right)\)
Dies ist bereits der richtige Ausdruck für die aus dem System gewonnene mechanische Arbeit. Die beim Carnot-Prozess gewonnene Arbeit wird nur durch die beiden isothermen Zustandsänderungen bestimmt.
Es ist jetzt noch weiter möglich, den obigen Term zu verkürzen, indem wir die Adiabatengleichungen für den 2. und 4. Takt betrachten. Die Adiabatengleichung für den 2. Takt lautet:
\(T_{1} \,\, \cdot \,\, V_{2}^{\,\,\,\, \kappa \,\, - \,\, 1} \,\, = \,\, T_{2} \,\, \cdot \,\, V_{3}^{\,\,\,\, \kappa \,\, - \,\, 1} \,\,\)
Für den 4. Takt lautet die Adiabatengleichung:
\(T_{2} \,\, \cdot \,\, V_{4}^{\,\,\,\, \kappa \,\, - \,\, 1} \,\, = \,\, T_{1} \,\, \cdot \,\, V_{1}^{\,\,\,\, \kappa \,\, - \,\, 1} \,\,\)
Aus beiden Gleichungen finden wir die Beziehung: \(\frac{T_{1}}{T_{2}} \,\, = \,\, \frac{V_{3}}{V_{2}} \,\, = \,\, \frac{V_{4}}{V_{1}}\) und damit: \(\,\, \frac{V_{2}}{V_{1}} \,\, = \,\, \frac{V_{3}}{V_{4}}\)
Wir ziehen beim 2. Term für den Ausdruck der Gesamtarbeit das negative Vorzeichen hervor und erhalten:
\(n \,\, \cdot \,\, R \,\, \cdot \,\, T_{1} \,\, \cdot ln \left( \frac{V_{2}}{V_{1}} \right) \,\, - \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, T_{2} \,\, \cdot ln \left( \frac{V_{3}}{V_{4}} \right)\)
Jetzt können wir aber durch die obige hergeleitete Beziehung: \(\,\, \frac{V_{2}}{V_{1}} \,\, = \,\, \frac{V_{3}}{V_{4}}\) schreiben:
\(W \,\, = \,\, n \,\, \cdot \,\, R \,\, \cdot \,\, \left( \frac{V_{2}}{V_{1}} \right) \,\, \cdot (\,\, T_{1} \,\, - \,\, T_{2})\)
Das ist nun der fertige Ausdruck für die gesamte aus dem System gewonnene Arbeit. Wichtig zu beachten ist, dass die Temperatur \(T_{1}\) größer ist als die Temperatur \(T_{2}\) (Durch die adiabatische Expansion des Gases im 2. Takt sinkt die Temperatur des Gases.)
Daher ist die Expansionsarbeit im 1. Takt größer als die Kompressionsarbeit im 3. Takt und wir erhalten in einem Zyklus eine gewisse mechanische Arbeit, welche das Gas nach außen abgibt.
|

